নোট
এই পৃষ্ঠাটি docs/tutorials/04_european_put_option_pricing.ipynb থেকে বানানো হয়েছে।
ইউরোপীয় পুট বিকল্পের মূল্য নির্ধারণ#
ভূমিকা#
ধরুন স্ট্রাইক প্রাইস সহ একটি ইউরোপীয় পুট বিকল্প \(K\) এবং একটি অন্তর্নিহিত সম্পদ যার পরিপক্কতায় স্পট মূল্য \(S_T\) একটি প্রদত্ত এলোমেলো বিতরণ অনুসরণ করে। সম্পর্কিত পেওফ ফাংশনটি হিসাবে সংজ্ঞায়িত করা হয়:
নিম্নে একটি মানের (অ্যামপ্লিটিউড) উপর নির্ভরশীল কোয়ান্টাম অ্যালগোরিদম ব্যবহার করে প্রত্যাশিত পেঅফ, যা হলো ছাড় দেয়ার আগের আদর্শমূল্য, অনুমান করা হয়েছে।
একই সাথে, সম্পর্কযুক্ত \(\Delta\) অর্থাৎ স্পট দামের সাপেক্ষে বিকল্প দামের অন্তরকলন এভাবে সংজ্ঞাযিত:
উদ্দেশ্য অন্বয়ের (অবজেক্টিভ ফাংশন) আনুমানিকতা এবং কোয়ান্টাম কম্পিউটারগুলিতে বিকল্প মূল্য নির্ধারণ এবং ঝুঁকি বিশ্লেষণের একটি সাধারণ ভূমিকা নিম্নলিখিত গবেষণাপত্রগুলোতে দেওয়া হয়েছে:
[1]:
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
from qiskit_algorithms import IterativeAmplitudeEstimation, EstimationProblem
from qiskit.circuit.library import LinearAmplitudeFunction
from qiskit_aer.primitives import Sampler
from qiskit_finance.circuit.library import LogNormalDistribution
অনিশ্চয়তা মডেল#
We construct a circuit to load a log-normal random distribution into a quantum state. The distribution is truncated to a given interval \([\text{low}, \text{high}]\) and discretized using \(2^n\) grid points, where \(n\) denotes the number of qubits used. The unitary operator corresponding to the circuit implements the following:
যেখানে math:p_i খণ্ডিত এবং বিযুক্ত বিতরণগুলির সম্ভাবনা বোঝায় এবং \(i\) অ্যাফাইন ম্যাপ ব্যবহার করে ডান ব্যবধানে ম্যাপ করা হয়েছে:
[2]:
# number of qubits to represent the uncertainty
num_uncertainty_qubits = 3
# parameters for considered random distribution
S = 2.0 # initial spot price
vol = 0.4 # volatility of 40%
r = 0.05 # annual interest rate of 4%
T = 40 / 365 # 40 days to maturity
# resulting parameters for log-normal distribution
mu = (r - 0.5 * vol**2) * T + np.log(S)
sigma = vol * np.sqrt(T)
mean = np.exp(mu + sigma**2 / 2)
variance = (np.exp(sigma**2) - 1) * np.exp(2 * mu + sigma**2)
stddev = np.sqrt(variance)
# lowest and highest value considered for the spot price; in between, an equidistant discretization is considered.
low = np.maximum(0, mean - 3 * stddev)
high = mean + 3 * stddev
# construct A operator for QAE for the payoff function by
# composing the uncertainty model and the objective
uncertainty_model = LogNormalDistribution(
num_uncertainty_qubits, mu=mu, sigma=sigma**2, bounds=(low, high)
)
[3]:
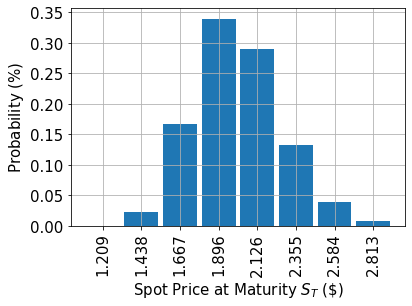
# plot probability distribution
x = uncertainty_model.values
y = uncertainty_model.probabilities
plt.bar(x, y, width=0.2)
plt.xticks(x, size=15, rotation=90)
plt.yticks(size=15)
plt.grid()
plt.xlabel("Spot Price at Maturity $S_T$ (\$)", size=15)
plt.ylabel("Probability ($\%$)", size=15)
plt.show()
মূল্যনির্ধারণ অন্বয়#
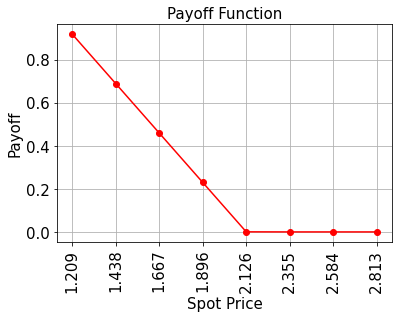
পেওফের কাজটি পরিপক্কতায় \(S_T\) বর্ধমান স্পট দামের সাথে রৈখিকভাবে হ্রাস পায় যতক্ষণ না এটি স্ট্রাইক দামের সমান স্পট দাম শূন্যে পৌঁছায় \(K\), এটি বড় স্পট দামের জন্য স্থির থাকে শূন্যের দিকে। প্রয়োগটি একটি তুলনাকারী ব্যবহার করে, এটি থেকে একটি অ্যানসিলা কিউবিট ফ্লিপ করে :math: big|0rangle থেকে: \(\big|1\rangle\) যদি \(S_T \leq K\), এবং এই অ্যানসিলাটি পেওফ ফাংশনের লিনিয়ার অংশ নিয়ন্ত্রণ করতে ব্যবহৃত হয়।.
রৈখিক অংশটি অনুমান করতে তারপর এই পদ্ধতি ব্যবহার করা হয় - ছোট মান এর \(|y|\) এর জন্যে \(\sin^2(y + \pi/4) \approx y + 1/2\) হয় যে কারণে যেকোনো প্রদত্ত আনুমানিক আরোহী গুণক (স্কেলিং factor) \(c_{approx} \in [0, 1]\) ও \(x \in [0, 1]\) এর জন্যে আমরা ধরি
for small \(c_\text{approx}\)
আমরা খুব সহজেই একটি চালক বানাতে পারি যেটা
নিয়ন্ত্রিত ওয়াই-ঘূর্ণন (Y-রোটেশন) ব্যবহার করে।
অবশেষে, আমরা শেষ কিউবিটে \(\big|1\rangle\) পরিমাপের সম্ভাবনাতে আগ্রহী, যেটা কিনা \(\sin^2(a*x+b)\) এর সাথে মিলে যাবার কথা। এই অনুমান গুলোর সাহায্যে আমরা আগ্রহের মানগুলির নিকটবর্তী মাত্রাগুলো পেয়ে যাবো। যত ছোট \(c_{approx}\) এর মান হবে, আমাদের প্রাপ্ত অনুমান তত ভালো হবে। কিন্তু এখানে এটাও মাথায় রাখা দরকার যে যেহেতু অনুমানটি \(c_{approx}\) এর ওপরে নির্ভর তাই মূল্যায়নের কিউবিটগুলির সংখ্যা \(m\) সেই অনুসারে সামঞ্জস্য করা দরকার।
অনুমান বিষয়ে বিশদে জানতে এই গবেষণাপত্রটি পড়ুন: Quantum Risk Analysis. Woerner, Egger. 2018.
[4]:
# set the strike price (should be within the low and the high value of the uncertainty)
strike_price = 2.126
# set the approximation scaling for the payoff function
rescaling_factor = 0.25
# setup piecewise linear objective fcuntion
breakpoints = [low, strike_price]
slopes = [-1, 0]
offsets = [strike_price - low, 0]
f_min = 0
f_max = strike_price - low
european_put_objective = LinearAmplitudeFunction(
num_uncertainty_qubits,
slopes,
offsets,
domain=(low, high),
image=(f_min, f_max),
breakpoints=breakpoints,
rescaling_factor=rescaling_factor,
)
# construct A operator for QAE for the payoff function by
# composing the uncertainty model and the objective
european_put = european_put_objective.compose(uncertainty_model, front=True)
[5]:
# plot exact payoff function (evaluated on the grid of the uncertainty model)
x = uncertainty_model.values
y = np.maximum(0, strike_price - x)
plt.plot(x, y, "ro-")
plt.grid()
plt.title("Payoff Function", size=15)
plt.xlabel("Spot Price", size=15)
plt.ylabel("Payoff", size=15)
plt.xticks(x, size=15, rotation=90)
plt.yticks(size=15)
plt.show()
[6]:
# evaluate exact expected value (normalized to the [0, 1] interval)
exact_value = np.dot(uncertainty_model.probabilities, y)
exact_delta = -sum(uncertainty_model.probabilities[x <= strike_price])
print("exact expected value:\t%.4f" % exact_value)
print("exact delta value: \t%.4f" % exact_delta)
exact expected value: 0.1709
exact delta value: -0.8193
প্রত্যাশিত বেতন মূল্যনির্ধারণ করো#
[7]:
# set target precision and confidence level
epsilon = 0.01
alpha = 0.05
problem = EstimationProblem(
state_preparation=european_put,
objective_qubits=[num_uncertainty_qubits],
post_processing=european_put_objective.post_processing,
)
# construct amplitude estimation
ae = IterativeAmplitudeEstimation(
epsilon_target=epsilon, alpha=alpha, sampler=Sampler(run_options={"shots": 100, "seed": 75})
)
[8]:
result = ae.estimate(problem)
[9]:
conf_int = np.array(result.confidence_interval_processed)
print("Exact value: \t%.4f" % exact_value)
print("Estimated value: \t%.4f" % (result.estimation_processed))
print("Confidence interval:\t[%.4f, %.4f]" % tuple(conf_int))
Exact value: 0.1709
Estimated value: 0.1770
Confidence interval: [0.1720, 0.1820]
ডেল্টা মূল্যায়ন করো।#
প্রত্যাশিত পেওফের চেয়ে ডেল্টা মূল্যায়ন করা কিছুটা সহজ। প্রত্যাশিত বেতন হিসাবে একইভাবে, আমরা কেসগুলি সনাক্ত করতে একটি তুলনামূলক সার্কিট এবং একটি অ্যান্সিলা কিউবিট ব্যবহার করি যেখানে \(S_T \leq K\). তবে, যেহেতু আমরা কেবলমাত্র এই অবস্থার সত্যতা হওয়ার (নেতিবাচক) সম্ভাবনা সম্পর্কে আগ্রহী, তাই আমরা আরও কিছুটা অনুমান ছাড়াই সরাসরি প্রশস্ততা অনুমানে এই আন্সিলার কিউবিটটি উদ্দেশ্য কিউবিট হিসাবে ব্যবহার করতে পারি।
[10]:
# setup piecewise linear objective fcuntion
breakpoints = [low, strike_price]
slopes = [0, 0]
offsets = [1, 0]
f_min = 0
f_max = 1
european_put_delta_objective = LinearAmplitudeFunction(
num_uncertainty_qubits,
slopes,
offsets,
domain=(low, high),
image=(f_min, f_max),
breakpoints=breakpoints,
)
# construct circuit for payoff function
european_put_delta = european_put_delta_objective.compose(uncertainty_model, front=True)
[11]:
# set target precision and confidence level
epsilon = 0.01
alpha = 0.05
problem = EstimationProblem(
state_preparation=european_put_delta, objective_qubits=[num_uncertainty_qubits]
)
# construct amplitude estimation
ae_delta = IterativeAmplitudeEstimation(
epsilon_target=epsilon, alpha=alpha, sampler=Sampler(run_options={"shots": 100, "seed": 75})
)
[12]:
result_delta = ae_delta.estimate(problem)
[13]:
conf_int = -np.array(result_delta.confidence_interval)[::-1]
print("Exact delta: \t%.4f" % exact_delta)
print("Estimated value: \t%.4f" % -result_delta.estimation)
print("Confidence interval: \t[%.4f, %.4f]" % tuple(conf_int))
Exact delta: -0.8193
Estimated value: -0.8197
Confidence interval: [-0.8236, -0.8158]
[14]:
import qiskit.tools.jupyter
%qiskit_version_table
%qiskit_copyright
Version Information
| Software | Version |
|---|---|
qiskit | None |
qiskit-terra | 0.45.0.dev0+c626be7 |
qiskit_aer | 0.12.0 |
qiskit_algorithms | 0.2.0 |
qiskit_finance | 0.4.0 |
qiskit_ibm_provider | 0.6.1 |
| System information | |
| Python version | 3.9.7 |
| Python compiler | GCC 7.5.0 |
| Python build | default, Sep 16 2021 13:09:58 |
| OS | Linux |
| CPUs | 2 |
| Memory (Gb) | 5.778430938720703 |
| Fri Aug 18 16:14:14 2023 EDT | |
This code is a part of Qiskit
© Copyright IBM 2017, 2023.
This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.
[ ]: