নোট
এই পৃষ্ঠাটি docs/tutorials/10_warm_start_qaoa.ipynb থেকে বানানো হয়েছে।
পোর্টফোলিও ডাইভারসিফিকেশন বা দপ্তর বৈচিত্র্যকরণ।#
ভূমিকা#
সম্পদ ব্যবস্থাপনায়, মূলত দুটি পন্থা রয়েছে: সক্রিয় এবং নিষ্ক্রিয় বিনিয়োগ ব্যবস্থাপনা। নিষ্ক্রিয় বিনিয়োগ ব্যবস্থাপনার মধ্যে, ইনডেক্স-ট্র্যাকিং ফান্ড রয়েছে এবং পোর্টফোলিও বৈচিত্র্যের উপর ভিত্তি করে পন্থা রয়েছে, যার লক্ষ্য হল অল্প সংখ্যক প্রতিনিধি স্টক দ্বারা বিপুল সংখ্যক সম্পদ সহ একটি পোর্টফোলিওকে প্রতিনিধিত্ব করা। এই নোটবুকটি একটি পোর্টফোলিও বৈচিত্র্যময় সমস্যার চিত্র তুলে ধরেছে, যা সম্প্রতি দুটি কারণে জনপ্রিয় হয়ে উঠেছে: ১. সীমিত লেনদেনের খরচে সীমিত বাজেটের মাধ্যমে একটি সূচকের (বা অনুরূপ সম্পদের সমষ্টি) কর্মক্ষমতা অনুকরণ করা সম্ভব করে তোলে। এটি হল: ঐতিহ্যগত সূচক-ট্র্যাকিং সূচকের সমস্ত সম্পদ কিনতে পারে, আদর্শভাবে সূচকের মতো একই ওজন সহ। এটি বেশ কয়েকটি কারণে অবাস্তব হতে পারে: সম্পত্তির প্রতি একক রাউন্ড লটের মোট পরিমাণ ব্যবস্থাপনার অধীনে সম্পদের চেয়ে বেশি হতে পারে, অখণ্ডতা সীমাবদ্ধতার সাথে সূচক-ট্র্যাকিং সমস্যার বৃহত আকার অপ্টিমাইজেশান সমস্যাটিকে কঠিন করে তুলতে পারে, এবং সূচকের ওজনগুলির সাথে অবস্থানগুলিকে সামঞ্জস্য করার জন্য ঘন ঘন পুনর্বিন্যাসের লেনদেনের খরচ পদ্ধতির ব্যয়বহুল হতে পারে। সুতরাং, একটি জনপ্রিয় পন্থা হল \(q\) সম্পদের একটি পোর্টফোলিও নির্বাচন করা যা \(n\) সম্পদের সাথে বাজারের প্রতিনিধিত্ব করে, যেখানে \(q\), \(n\) এর তুলনায় উল্লেখযোগ্যভাবে ছোট, কিন্তু যেখানে পোর্টফোলিও অন্তর্নিহিত বাজারের আচরণের প্রতিলিপি করে। কিভাবে \(q\) ক্লাস্টারে সম্পদগুলিকে গ্রুপ করা যায় এবং কোন \(q\) সম্পদের \(q\) ক্লাস্টারের প্রতিনিধিত্ব করা উচিত তা নির্ধারণ করার জন্য একটি বড় আকারের অপ্টিমাইজেশান সমস্যা সমাধানের জন্য নিচে আমরা সেই পোর্টফোলিও বৈচিত্র্য সমস্যার জন্য গাণিতিক মডেল বর্ণনা করেছি [Cornuejols & Tutuncu, 2006] ২-এ প্রবর্তিত হিসাবে। লক্ষ্য করুন যে ঐতিহ্যগতভাবে, আধুনিক পোর্টফোলিও তত্ত্ব কোভারিয়েন্স ম্যাট্রিক্সকে সম্পদের মধ্যে মিলের একটি পরিমাপ হিসাবে বিবেচনা করে। যেমন, যাইহোক, কোভারিয়েন্স ম্যাট্রিক্স অসম্পূর্ণ। উদাহরণস্বরূপ, লন্ডন এবং নিউইয়র্কে তালিকাভুক্ত একটি কোম্পানি বিবেচনা করুন। যদিও উভয় তালিকা খুব অনুরূপ হওয়া উচিত, দুটি তালিকার দামের সময় সিরিজের কিছু অংশ ওভারল্যাপ হবে, কারণ বাজারগুলি খোলা সময়ের আংশিক ওভারল্যাপের কারণে। কোভারিয়েন্স এর পরিবর্তে, কেউ বিবেচনা করতে পারে, উদাহরণস্বরূপ, [Berndt and Clifford, 1994] এর গতিশীল টাইম ওয়ারপিংকে দুই টাইম সিরিজের মধ্যে মিলের পরিমাপ হিসাবে বিবেচনা করা যেতে পারে, যা কিছু সময়ের জন্য, ডেটা শুধুমাত্র একটি দ্বারা ধরা হয় সময় সিরিজ, অন্যদের জন্য, উভয় সময় সিরিজ স্টক মূল্যের সমান্তরাল বিবর্তনের কারণে মিল দেখায়।
সামগ্রিকভাবে আমাদের প্রদর্শিত কর্মধারা গঠিত হয়:
সম্পদের ভিত্তি (গ্রাউন্ড) সেট বাছাই করুন। আমাদের ক্ষেত্রে, এটি একটি অল্প সংখ্যক মার্কিন স্টক।
সম্পদের দামের বিবর্তনকে ধারণ করে সময় সিরিজ লোড করুন। আমাদের ক্ষেত্রে, এটি উইকিপিডিয়া বা Nasdaq বা LSE বা EuroNext থেকে সামঞ্জস্যকৃত দৈনিক সমাপনী মূল্যের তথ্যগুলির একটি সরল লোড, যেখানে একটি বাস্তব সম্পদ ব্যবস্থাপনায়, অনেক বেশি ফ্রিকোয়েন্সি বিবেচনা করা যেতে পারে
টাইম সিরিজের মধ্যে জোড়া-ভিত্তিক মিল গণনা করুন। আমাদের ক্ষেত্রে, আমরা এখনও ক্লাসিক্যাল কম্পিউটারে ডাইনামিক টাইম ওয়ারপিং এর রৈখিক-টাইম আনুমানিকতা চালাই।
এর প্রকৃত পোর্টফোলিও গণনা করুন \(q\) প্রতিনিধি সম্পদ, মিলের পরিমাপের উপর ভিত্তি করে। এই ধাপটি আসলে দুবার চালানো হয়। প্রথমত, আমরা ক্লাসিক্যাল কম্পিউটারে একটি IBM solver (IBM ILOG CPLEX বা Exact Eigensolver) দ্বারা একটি রেফারেন্স ভ্যালু পাই। দ্বিতীয়ত, আমরা একটি বিকল্প, হাইব্রিড অ্যালগরিদম আংশিকভাবে কোয়ান্টাম কম্পিউটারে চালাই।
ফলাফল দৃশ্যায়ন বা চিত্রায়ন। আমাদের ক্ষেত্রে, এটি আবার একটি সহজ সরল লেখচিত্র (প্লট)।
এটিতে আমরা পূর্ব প্রয়োজনীয় জিনিসগুলোর ইনস্টলেশন এবং ডেটা লোডিং করার আগে প্রথমে ওপরে (৪) ব্যবহৃত মডেলটিকে বর্ণনা করবো।
মডেল(নকশা)#
[Cornuejols & Tutuncu, 2006] এ আলোচনা করা হয়েছে, আমরা একটি গাণিতিক মডেল বর্ণনা করি যা সম্পদগুলিকে একই রকমের গোষ্ঠীতে বিভক্ত করে এবং প্রতিটি গ্রুপ থেকে একটি প্রতিনিধি সম্পদ নির্বাচন করে সূচক তহবিলের পোর্টফোলিওতে অন্তর্ভুক্ত করা হয়। মডেলটি নিম্নলিখিত ডেটার উপর ভিত্তি করে তৈরি করা হয়েছে, যা আমরা পরে আরও বিস্তারিতভাবে আলোচনা করব:
উদাহরণস্বরূপ, \(i \neq j\) এর জন্য \(\rho_{ii} = 1\), \(\rho_{ij} \leq 1\) এবং অন্যান্য সদৃশ স্টকস এর জন্য \(\rho_{ij}\) এর মান বৃহত্তর । এর একটি উদাহরণ হল স্টকস এর রিটার্ন \(i\) এবং \(j\) এর মধ্যেকার সম্পর্ক বা কোরিলেশন। কিন্তু কেউ অন্য সাদৃশ্য সূচক বা সিমিলারিটি ইনডেক্স \(\rho_{ij}\) বেছে নিতে পারে।
আমরা যে সমস্যা সমাধানে আগ্রহী সেটা হল:
ক্লাস্টারিং সীমাবদ্ধতা সাপেক্ষে:
ধারাবাহিকতা সীমাবদ্ধতা সাপেক্ষে:
এবং সমাকলন সীমাবদ্ধতা সাপেক্ষে:
\(y_j\) ভেরিয়েবলগুলি বর্ণনা করে যে কোন স্টক \(j\) ইনডেক্স ফান্ডে আছে (\(y_j\) হবে যদি \(j\) ফান্ডে নির্বাচন করা হয়, অন্যথায় \(0\))। প্রতিটি স্টক \(i = 1,\dots,n\)- এর জন্য, চল রাশি \(x_{ij}\) ইঙ্গিত করে যে সূচক তহবিলে কোন স্টক \(j\) সবচেয়ে বেশি \(i\) এর সাথে মিলে (\(x_{ij} = 1\) যদি \(j\) সূচক তহবিলে সবচেয়ে অনুরূপ স্টক হয়, অন্যথায় \(0\)).
প্রথম সীমাবদ্ধতা নির্বাচন করে তহবিলে \(q\) স্টক। দ্বিতীয় সীমাবদ্ধতা আরোপ করে যে প্রতিটি স্টক \(i\) এর ঠিক একটি প্রতিনিধি স্টক রয়েছে \(j\) তহবিলে। তৃতীয় এবং চতুর্থ সীমাবদ্ধতা নিশ্চিত করে যে স্টক \(i\) স্টক দ্বারা গণিত করা যেতে পারে \(j\) শুধুমাত্র যদি \(j\) তহবিলে থাকে। মডেলের উদ্দেশ্য \(n\) স্টক এবং তহবিলে তাদের প্রতিনিধিদের মধ্যে মিলটি সর্বাধিক করে। বিভিন্ন খরচ ফাংশন এছাড়াও বিবেচনা করা যেতে পারে।
আসুন একটি ভেক্টরে সিদ্ধান্তের ভেরিয়েবলগুলিকে একত্রিত করি
যার মাত্রা হল \({\bf z} \in \{0,1\}^N\), সাথে \(N = n (n+1)\) এবং এর সাথে অনুকূল সমাধান নির্দেশ করুন \({\bf z}^*\), এবং সর্বাপেক্ষা কাম্য খরচ \(f^*\)।
একটি হাইব্রিড পদ্ধতি#
এখানে, আমরা Farhi, Goldstone, and Gutmann (2014) এর কোয়ান্টাম আনুমানিক অপ্টিমাইজেশন পদ্ধতির অনুসরণ করে শাস্ত্রীয় এবং কোয়ান্টাম কম্পিউটিং ধাপগুলিকে একত্রিত করে এমন একটি পদ্ধতি প্রদর্শন করি।
একটি দ্বিমিক বহুরাশিক অনুকূলকরণ (অপটিমাইজেশন) তৈরি করুন#
\((M)\) থেকে কেউ সমতা সীমাবদ্ধতার সাথে একটি বাইনারি বহুপদী অপ্টিমাইজেশান তৈরি করতে পারে, \(x_{ij} (1- y_j) = 0\) সমতা সীমাবদ্ধতা দিয়ে \(x_{ij} \leq y_j\) বৈষম্য সীমাবদ্ধতা প্রতিস্থাপন করে। তারপর সমস্যা হয়ে যায়:
ক্লাস্টারিং সীমাবদ্ধতা, সমাকলন সীমাবদ্ধতা, এবং নিচের পরিবর্তিত ধারাবাহিকতা সীমাবদ্ধতা সাপেক্ষে:
আইসিং হ্যামিল্টোনীয়ান নির্মাণ করুন#
আমরা এখন পেনাল্টি পদ্ধতি দ্বারা আইসিং হ্যামিল্টোনিয়ান (QUBO) তৈরি করতে পারি (সমতা প্রতিবন্ধকতার জন্য একটি পেনাল্টি সহগ \(A\) প্রবর্তন) হিসাবে
হ্যামিল্টোনিয়ান থেকে দ্বিঘাত (কোয়াড্রাটিক) প্রোগ্রামিং (QP) গঠন বা ফর্মুলেশন।#
\({\bf z}\) ভেক্টরটিতে, আইসিং হ্যামিল্টোনিয়ান উপাদানগুলিকে এভাবে লেখা যেতে পারে,
প্রথম পদ বা টার্ম:
দ্বিতীয় পদ:
তৃতীয় পদ:
যেটির প্রায় সমান হল:
চতুর্থ পদ বা টার্ম:
পঞ্চম পদ বা টার্ম:
অতএব, ফর্মুলেশন বা প্রস্তুতিটি হয়ে যায়,
যেটিকে ভেরিয়েশনাল কোয়ান্টাম আইগেনসলভার (ভিকিউই) এ পাস করা যায়।
তথ্যসূত্র (রেফারেন্স)#
[1] G. Cornuejols, M. L. Fisher, and G. L. Nemhauser, Location of bank accounts to optimize float: an analytical study of exact and approximate algorithms, Management Science, vol. 23(8), 1997
[2] E. Farhi, J. Goldstone, S. Gutmann e-print arXiv 1411.4028, 2014
[3] অপটিমাইজেশন মেথড ইন ফাইন্যান্স G. Cornuejols and R. Tutuncu, Optimization methods in finance, 2006
[4] DJ. Berndt and J. Clifford, Using dynamic time warping to find patterns in time series. In KDD workshop 1994 (Vol. 10, No. 16, pp. 359-370).
রূপায়ণ (ইমপ্লিমেন্টেশন)#
প্রথমে, আমরা প্রয়োজনীয় মডিউল ইম্পোর্ট বা আনয়ন করলাম।
[1]:
# Import requisite modules
import math
import datetime
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# Import Qiskit packages
from qiskit.circuit.library import TwoLocal
from qiskit_aer.primitives import Sampler
from qiskit_algorithms import NumPyMinimumEigensolver, QAOA, SamplingVQE
from qiskit_algorithms.optimizers import COBYLA
from qiskit_optimization.algorithms import MinimumEigenOptimizer
# The data providers of stock-market data
from qiskit_finance.data_providers import RandomDataProvider
from qiskit_finance.applications.optimization import PortfolioDiversification
পরবর্তীতে, আমরা দুটি স্টকের জন্য মূল্য তথ্য ডাউনলোড করি এবং তাদের জোড়া-ভিত্তিক মিল ম্যাট্রিক্স (dynamic time warping বিপরীত গ্রহণের মাধ্যমে দূরত্বকে (0,1] এ নরমালাইজ) নির্ণয় করি। যদি এটি ব্যর্থ হয়, যেমন, আপনি অফলাইনে থাকার কারণে বা স্টক-মার্কেট ডেটা অ্যাক্সেসের দৈনিক সীমা অতিক্রম করার কারণে, আমরা পরিবর্তে একটি ধ্রুবক ম্যাট্রিক্স বিবেচনা করি।
[2]:
# Generate a pairwise time-series similarity matrix
seed = 123
stocks = ["TICKER1", "TICKER2"]
n = len(stocks)
data = RandomDataProvider(
tickers=stocks,
start=datetime.datetime(2016, 1, 1),
end=datetime.datetime(2016, 1, 30),
seed=seed,
)
data.run()
rho = data.get_similarity_matrix()
এখন আমরা গুচ্ছ সংখ্যা নির্ধারণ করি। এটি আমাদের লোড করা স্টকের সংখ্যার চেয়ে ছোট হতে হবে।
[3]:
q = 1 # q less or equal than n
প্রথাগত (ক্লাসিক্যাল) সমাধান IBM ILOG CPLEX ব্যাবহার করে।#
একটি প্রথাগত (ক্লাসিক্যাল) সমাধানের জন্য, আমরা আই.বি.এম সি.পি.এল. ই.এক্স (IBM CPLEX) ব্যবহার করি। সি.পি.এল.ই.এক্স এই সমস্যার সঠিক সমাধান খুঁজে পেতে সক্ষম। আমরা প্রথমে একটি প্রথাগত (ক্লাসিক্যাল) অপ্টিমাইজার শ্রেণি সংজ্ঞায়িত করি যা এমনভাবে সমস্যাটিকে এনকোড করে যাতে সিপিএলএক্স সমাধান করতে পারে এবং তারপরে ক্লাসটি তাৎক্ষণিক এবং সেটি সমাধান করে।
[4]:
class ClassicalOptimizer:
def __init__(self, rho, n, q):
self.rho = rho
self.n = n # number of inner variables
self.q = q # number of required selection
def compute_allowed_combinations(self):
f = math.factorial
return int(f(self.n) / f(self.q) / f(self.n - self.q))
def cplex_solution(self):
# refactoring
rho = self.rho
n = self.n
q = self.q
my_obj = list(rho.reshape(1, n**2)[0]) + [0.0 for x in range(0, n)]
my_ub = [1 for x in range(0, n**2 + n)]
my_lb = [0 for x in range(0, n**2 + n)]
my_ctype = "".join(["I" for x in range(0, n**2 + n)])
my_rhs = (
[q]
+ [1 for x in range(0, n)]
+ [0 for x in range(0, n)]
+ [0.1 for x in range(0, n**2)]
)
my_sense = (
"".join(["E" for x in range(0, 1 + n)])
+ "".join(["E" for x in range(0, n)])
+ "".join(["L" for x in range(0, n**2)])
)
try:
my_prob = cplex.Cplex()
self.populatebyrow(my_prob, my_obj, my_ub, my_lb, my_ctype, my_sense, my_rhs)
my_prob.solve()
except CplexError as exc:
print(exc)
return
x = my_prob.solution.get_values()
x = np.array(x)
cost = my_prob.solution.get_objective_value()
return x, cost
def populatebyrow(self, prob, my_obj, my_ub, my_lb, my_ctype, my_sense, my_rhs):
n = self.n
prob.objective.set_sense(prob.objective.sense.minimize)
prob.variables.add(obj=my_obj, lb=my_lb, ub=my_ub, types=my_ctype)
prob.set_log_stream(None)
prob.set_error_stream(None)
prob.set_warning_stream(None)
prob.set_results_stream(None)
rows = []
col = [x for x in range(n**2, n**2 + n)]
coef = [1 for x in range(0, n)]
rows.append([col, coef])
for ii in range(0, n):
col = [x for x in range(0 + n * ii, n + n * ii)]
coef = [1 for x in range(0, n)]
rows.append([col, coef])
for ii in range(0, n):
col = [ii * n + ii, n**2 + ii]
coef = [1, -1]
rows.append([col, coef])
for ii in range(0, n):
for jj in range(0, n):
col = [ii * n + jj, n**2 + jj]
coef = [1, -1]
rows.append([col, coef])
prob.linear_constraints.add(lin_expr=rows, senses=my_sense, rhs=my_rhs)
[5]:
# Instantiate the classical optimizer class
classical_optimizer = ClassicalOptimizer(rho, n, q)
# Compute the number of feasible solutions:
print("Number of feasible combinations= " + str(classical_optimizer.compute_allowed_combinations()))
# Compute the total number of possible combinations (feasible + unfeasible)
print("Total number of combinations= " + str(2 ** (n * (n + 1))))
Number of feasible combinations= 2
Total number of combinations= 64
[6]:
# Visualize the solution
def visualize_solution(xc, yc, x, C, n, K, title_str):
plt.figure()
plt.scatter(xc, yc, s=200)
for i in range(len(xc)):
plt.annotate(i, (xc[i] + 0.015, yc[i]), size=16, color="r")
plt.grid()
for ii in range(n**2, n**2 + n):
if x[ii] > 0:
plt.plot(xc[ii - n**2], yc[ii - n**2], "r*", ms=20)
for ii in range(0, n**2):
if x[ii] > 0:
iy = ii // n
ix = ii % n
plt.plot([xc[ix], xc[iy]], [yc[ix], yc[iy]], "C2")
plt.title(title_str + " cost = " + str(int(C * 100) / 100.0))
plt.show()
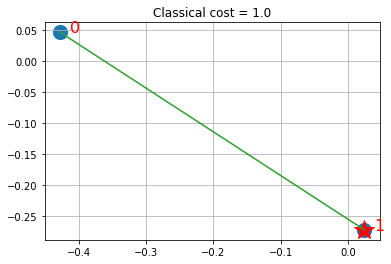
সমাধানটি নির্বাচিত স্টকগুলিকে তারার মাধ্যমে এবং সবুজ রঙে (মিলের মাধ্যমে) অন্যান্য স্টকগুলির সাথে দেখায় যা লিঙ্কযুক্ত স্টক দ্বারা তহবিলে প্রতিনিধিত্ব করে।
Quantum Computing solution using Qiskit#
কোয়ান্টাম সমাধানের জন্য, আমরা Qiskit ব্যবহার করি। আমরা প্রথমে একটি ক্লাস কোয়ান্টাম অপটিমাইজার সংজ্ঞায়িত করি যা সমস্যা সমাধানের জন্য কোয়ান্টাম পদ্ধতির এনকোড করে এবং তারপর আমরা তা তাৎক্ষণিক সমাধান করি। আমরা ক্লাসের ভিতরে নিম্নলিখিত পদ্ধতিগুলি সংজ্ঞায়িত করি:
"exact_solution": আইসিং হ্যামিল্টোনিয়ান সঠিকভাবে এনকোড করা আছে তা নিশ্চিত করার জন্য \(Z\) ভিত্তিতে, আমরা এর eigendecomposition গণনা করতে পারি ক্লাসিকভাবে, অর্থাৎ, মাত্রার একটি প্রতিসম ম্যাট্রিক্স বিবেচনা করে \(2^N \times 2^N\)। নিকট সমস্যার জন্য \(n=3\), অর্থাৎ \(N = 12\), মনে হয় অনেক ল্যাপটপের সীমা;
sampling_vqe_solution: solves the problem \((M)\) via the Sampling Variational Quantum Eigensolver (SamplingVQE);qaoa_solution: solves the problem \((M)\) via a Quantum Approximate Optimization Algorithm (QAOA).
[7]:
from qiskit_algorithms.utils import algorithm_globals
class QuantumOptimizer:
def __init__(self, rho, n, q):
self.rho = rho
self.n = n
self.q = q
self.pdf = PortfolioDiversification(similarity_matrix=rho, num_assets=n, num_clusters=q)
self.qp = self.pdf.to_quadratic_program()
# Obtains the least eigenvalue of the Hamiltonian classically
def exact_solution(self):
exact_mes = NumPyMinimumEigensolver()
exact_eigensolver = MinimumEigenOptimizer(exact_mes)
result = exact_eigensolver.solve(self.qp)
return self.decode_result(result)
def sampling_vqe_solution(self):
algorithm_globals.random_seed = 100
cobyla = COBYLA()
cobyla.set_options(maxiter=250)
ry = TwoLocal(n, "ry", "cz", reps=5, entanglement="full")
svqe_mes = SamplingVQE(sampler=Sampler(), ansatz=ry, optimizer=cobyla)
svqe = MinimumEigenOptimizer(svqe_mes)
result = svqe.solve(self.qp)
return self.decode_result(result)
def qaoa_solution(self):
algorithm_globals.random_seed = 1234
cobyla = COBYLA()
cobyla.set_options(maxiter=250)
qaoa_mes = QAOA(sampler=Sampler(), optimizer=cobyla, reps=3)
qaoa = MinimumEigenOptimizer(qaoa_mes)
result = qaoa.solve(self.qp)
return self.decode_result(result)
def decode_result(self, result, offset=0):
quantum_solution = 1 - (result.x)
ground_level = self.qp.objective.evaluate(result.x)
return quantum_solution, ground_level
ধাপ 1#
কোয়ান্টাম অনুকূলায়ক ক্লাসকে মুহূর্তায়িত বা ইনস্ট্যান্টিয়েট করুন পরামিতির দ্বারা: সদৃশ ম্যাট্রিক্স rho;- n এবং q তে অ্যাসেট এবং ক্লাস্টার এর সংখ্যা;
[8]:
# Instantiate the quantum optimizer class with parameters:
quantum_optimizer = QuantumOptimizer(rho, n, q)
ধাপ 2#
দ্বিমিক (বাইনারি) সুত্র বা গঠনের (আইএইচ-কিউপি) হিসাবে সমস্যাটি এনকোড করুন।
স্যানিটি বা সদ্বিবেচনা পরীক্ষা: নিশ্চিত করুন যে কোয়ান্টাম অপ্টিমাইজারে দ্বিমিক (বাইনারি) সূত্র বা গঠন সঠিক কিনা (যেমন, একই সমাধানের জন্যে একই ব্যয় হয়)।
[9]:
# Check if the binary representation is correct. This requires CPLEX
try:
import cplex
# warnings.filterwarnings('ignore')
quantum_solution, quantum_cost = quantum_optimizer.exact_solution()
print(quantum_solution, quantum_cost)
classical_solution, classical_cost = classical_optimizer.cplex_solution()
print(classical_solution, classical_cost)
if np.abs(quantum_cost - classical_cost) < 0.01:
print("Binary formulation is correct")
else:
print("Error in the formulation of the Hamiltonian")
except Exception as ex:
print(ex)
[0. 1. 0. 1. 0. 1.] 1.000779571614484
[1. 0. 1. 0. 1. 0.] 1.000779571614484
Binary formulation is correct
ধাপ 3#
সমস্যাটিকে Z বেসিসে বা ভিত্তিতে একটি আইসিং হ্যামিল্টোনিয়ান হিসেবে এনকোড করুন।
স্যানিটি বা সদ্বিবেচনা পরীক্ষা: নিশ্চিত করুন যে ফর্মূলেশন বা গঠনটি সঠিক কিনা (অর্থাৎ, একই সমাধানের জন্যে একই ব্যয় হয়)।
[10]:
ground_state, ground_level = quantum_optimizer.exact_solution()
print(ground_state)
classical_cost = 1.000779571614484 # obtained from the CPLEX solution
try:
if np.abs(ground_level - classical_cost) < 0.01:
print("Ising Hamiltonian in Z basis is correct")
else:
print("Error in the Ising Hamiltonian formulation")
except Exception as ex:
print(ex)
[0. 1. 0. 1. 0. 1.]
Ising Hamiltonian in Z basis is correct
ধাপ 4#
Solve the problem via SamplingVQE. Notice that depending on the number of qubits, this can take a while: for 6 qubits it takes 15 minutes on a 2015 Macbook Pro, for 12 qubits it takes more than 12 hours. For longer runs, logging may be useful to observe the workings; otherwise, you just have to wait until the solution is printed.
[11]:
svqe_state, svqe_level = quantum_optimizer.sampling_vqe_solution()
print(svqe_state, svqe_level)
try:
if np.linalg.norm(ground_state - svqe_state) < 0.01:
print("SamplingVQE produces the same solution as the exact eigensolver.")
else:
print(
"SamplingVQE does not produce the same solution as the exact eigensolver, but that is to be expected."
)
except Exception as ex:
print(ex)
[0. 1. 0. 1. 0. 1.] 1.000779571614484
SamplingVQE produces the same solution as the exact eigensolver.
ধাপ 5#
সমাধানটি দৃশ্যায়িত করা
[12]:
xc, yc = data.get_coordinates()
[13]:
visualize_solution(xc, yc, ground_state, ground_level, n, q, "Classical")
[14]:
visualize_solution(xc, yc, svqe_state, svqe_level, n, q, "SamplingVQE")
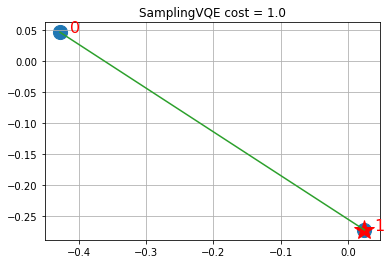
Solution shows the selected stocks via the stars and in green the links (via similarities) with other stocks that are represented in the fund by the linked stock. Keep in mind that SamplingVQE is a heuristic working on the QP formulation of the Ising Hamiltonian, though. For suitable choices of A, local optima of the QP formulation will be feasible solutions to the ILP (integer linear program). While for some small instances, as above, we can find optimal solutions of the QP formulation which coincide with optima of the ILP, finding optimal solutions of the ILP is harder than finding local optima of the QP formulation, in general. Even within the SamplingVQE, one may provide stronger guarantees, for specific variational forms (trial wave functions).
[15]:
import qiskit.tools.jupyter
%qiskit_version_table
%qiskit_copyright
Version Information
| Software | Version |
|---|---|
qiskit | 0.45.0.dev0+ea871e0 |
qiskit_optimization | 0.6.0 |
qiskit_finance | 0.4.0 |
qiskit_algorithms | 0.3.0 |
qiskit_aer | 0.12.2 |
qiskit_ibm_provider | 0.7.0 |
| System information | |
| Python version | 3.9.7 |
| Python compiler | GCC 7.5.0 |
| Python build | default, Sep 16 2021 13:09:58 |
| OS | Linux |
| CPUs | 2 |
| Memory (Gb) | 5.7784271240234375 |
| Tue Sep 05 15:08:55 2023 EDT | |
This code is a part of Qiskit
© Copyright IBM 2017, 2023.
This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.
[ ]: