Nota
Esta página fue generada a partir de docs/tutorials/01_neural_networks.ipynb.
Redes Neuronales Cuánticas#
Descripción General#
Este cuaderno muestra diferentes implementaciones de redes neuronales cuánticas (quantum neural network, QNN) proporcionadas en qiskit-machine-learning, y cómo se pueden integrar en flujos de trabajo básicos de machine learning cuántico (quantum machine learning, QML).
El tutorial está estructurado de la siguiente manera:
1. Introducción#
1.1. Redes Neuronales Cuánticas vs. Clásicas#
Las redes neuronales clásicas son modelos algorítmicos inspirados en el cerebro humano que se pueden entrenar para reconocer patrones en los datos y aprender a resolver problemas complejos. Se basan en una serie de nodos interconectados, o neuronas, organizados en una estructura en capas, con parámetros que se pueden aprender aplicando estrategias de entrenamiento de machine learning o deep learning.
La motivación detrás del machine learning cuántico (QML) es integrar nociones de computación cuántica y de machine learning clásico para abrir el camino a esquemas de aprendizaje nuevos y mejorados. Las QNNs aplican este principio genérico al combinar redes neuronales clásicas y circuitos cuánticos parametrizados. Debido a que se encuentran en una intersección entre dos campos, las QNNs se pueden ver desde dos perspectivas:
Desde una perspectiva de machine learning, las QNNs son, una vez más, modelos algorítmicos que se pueden entrenar para encontrar patrones ocultos en los datos de manera similar a sus contrapartes clásicas. Estos modelos pueden cargar datos clásicos (entradas) en un estado cuántico, y luego procesarlos con compuertas cuánticas parametrizadas por pesos entrenables. La Figura 1 muestra un ejemplo genérico de QNN que incluye los pasos de carga y procesamiento de datos. La salida de la medición de este estado se puede conectar a una función de pérdida para entrenar los pesos (ponderaciones) a través de la retropropagación.
Desde la perspectiva de la computación cuántica, las QNNs son algoritmos cuánticos basados en circuitos cuánticos parametrizados que se pueden entrenar de forma variacional utilizando optimizadores clásicos. Estos circuitos contienen un mapa de características (con parámetros de entrada) y un ansatz (con pesos entrenables), como se ve en la Figura 1.
Figura 1. Estructura genérica de una red neuronal cuántica (QNN).
Como puedes ver, estas dos perspectivas son complementarias y no necesariamente se basan en definiciones estrictas de conceptos como «neurona cuántica» o lo que constituye una «capa» de QNN.
1.2. Implementación en qiskit-machine-learning#
Las QNNs en qiskit-machine-learning están pensadas como unidades computacionales independientes de la aplicación en las que se pueden usar para diferentes casos de uso, y su configuración dependerá de la aplicación para la que se necesiten. El módulo contiene una interfaz para las QNNs y dos implementaciones específicas:
NeuralNetwork: La interfaz para redes neuronales. Esta es una clase abstracta de la que heredan todas las QNN.
EstimatorQNN: Una red basada en la evaluación de observables mecánicos cuánticos.
SamplerQNN: Una red basada en las muestras resultantes de medir un circuito cuántico.
Estas implementaciones se basan en las primitivas de qiskit. Las primitivas son el punto de entrada para ejecutar QNNs en un simulador o en hardware cuántico real. Cada implementación, EstimatorQNN y SamplerQNN, toma una instancia opcional de su primitiva correspondiente, que puede ser cualquier subclase de BaseEstimator y BaseSampler, respectivamente.
El módulo qiskit.primitives proporciona una implementación de referencia para las clases Sampler y Estimator para ejecutar simulaciones de vectores de estado. De forma predeterminada, si no se pasa ninguna instancia a una clase QNN, la red crea automáticamente una instancia de la primitiva de referencia correspondiente (Sampler o Estimator). Para obtener más información sobre las primitivas, consulta la documentación de las primitivas.
La clase NeuralNetwork es la interfaz para todas las QNNs disponibles en qiskit-machine-learning. Expone un paso hacia adelante y hacia atrás que toman muestras de datos y pesos entrenables como entrada.
Es importante tener en cuenta que las NeuralNetworks son «sin estado». No contienen ninguna capacidad de entrenamiento (estas se envían a los algoritmos o aplicaciones reales: classifiers, regressors, etc), ni almacenan los valores de los pesos entrenables.
Veamos ahora ejemplos específicos para las dos implementaciones de NeuralNetwork. Pero primero, configuremos la semilla algorítmica para garantizar que los resultados no cambien entre ejecuciones.
[25]:
from qiskit_algorithms.utils import algorithm_globals
algorithm_globals.random_seed = 42
2. Cómo Instanciar QNNs#
2.1. EstimatorQNN#
La EstimatorQNN toma como entrada un circuito cuántico parametrizado, así como un observable mecánico cuántico opcional, y genera cálculos de valor esperado para el paso hacia adelante. La EstimatorQNN también acepta listas de observables para construir QNNs más complejas.
Veamos una EstimatorQNN en acción con un ejemplo simple. Comenzamos construyendo el circuito parametrizado. Este circuito cuántico tiene dos parámetros, uno representa una entrada QNN y el otro representa un peso entrenable:
[26]:
from qiskit.circuit import Parameter
from qiskit import QuantumCircuit
params1 = [Parameter("input1"), Parameter("weight1")]
qc1 = QuantumCircuit(1)
qc1.h(0)
qc1.ry(params1[0], 0)
qc1.rx(params1[1], 0)
qc1.draw("mpl")
[26]:
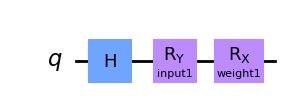
Ahora podemos crear un observable para definir el cálculo del valor esperado. Si no se establece, EstimatorQNN creará automáticamente el observable predeterminado \(Z^{\otimes n}\). Aquí, \(n\) es el número de qubits del circuito cuántico.
En este ejemplo, cambiaremos las cosas y usaremos el observable \(Y^{\otimes n}\):
[27]:
from qiskit.quantum_info import SparsePauliOp
observable1 = SparsePauliOp.from_list([("Y" * qc1.num_qubits, 1)])
Junto con el circuito cuántico definido anteriormente y el observable que hemos creado, el constructor de EstimatorQNN toma los siguientes argumentos de palabras clave:
estimator: instancia primitiva opcionalinput_params: lista de parámetros de circuitos cuánticos que deben tratarse como «entradas de red»weight_params: lista de parámetros de circuitos cuánticos que deben tratarse como «pesos de red»
En este ejemplo, previamente decidimos que el primer parámetro de params1 debería ser la entrada, mientras que el segundo debería ser el peso. Como estamos realizando una simulación de vector de estado local, no estableceremos el parámetro estimator; la red creará una instancia de la primitiva Estimator de referencia para nosotros. Si necesitáramos acceder a recursos en la nube o simuladores Aer, tendríamos que definir las respectivas instancias de Estimator y pasarlas al EstimatorQNN.
[28]:
from qiskit_machine_learning.neural_networks import EstimatorQNN
estimator_qnn = EstimatorQNN(
circuit=qc1, observables=observable1, input_params=[params1[0]], weight_params=[params1[1]]
)
estimator_qnn
[28]:
<qiskit_machine_learning.neural_networks.estimator_qnn.EstimatorQNN at 0x7fd668ca0e80>
Veremos cómo usar la QNN en las siguientes secciones, pero antes de eso, veamos la clase SamplerQNN.
2.2. SamplerQNN#
La SamplerQNN se instancia de manera similar a la EstimatorQNN, pero debido a que consume muestras directamente al medir el circuito cuántico, no requiere un observable personalizado.
Estas muestras de salida se interpretan por defecto como las probabilidades de medir el índice entero correspondiente a una cadena de bits. Sin embargo, SamplerQNN también nos permite especificar una función interpret para post-procesar las muestras. Esta función debe definirse de modo que tome un entero medido (de una cadena de bits) y lo asigne a un nuevo valor, es decir, un entero no negativo.
(!) Es importante tener en cuenta que si se define una función interpret personalizada, la red no puede inferir output_shape y debe proporcionarse explícitamente.
(!) También es importante tener en cuenta que si no se usa la función interpret, la dimensión del vector de probabilidad escalará exponencialmente con el número de qubits. Con una función interpret personalizada, esta escala puede cambiar. Si, por ejemplo, se asigna un índice a la paridad de la cadena de bits correspondiente, es decir, a 0 o 1, el resultado será un vector de probabilidad de longitud 2 independientemente del número de qubits.
Vamos a crear un circuito cuántico diferente para SamplerQNN. En este caso tendremos dos parámetros de entrada y cuatro pesos entrenables que parametrizan un circuito two-local.
[29]:
from qiskit.circuit import ParameterVector
inputs2 = ParameterVector("input", 2)
weights2 = ParameterVector("weight", 4)
print(f"input parameters: {[str(item) for item in inputs2.params]}")
print(f"weight parameters: {[str(item) for item in weights2.params]}")
qc2 = QuantumCircuit(2)
qc2.ry(inputs2[0], 0)
qc2.ry(inputs2[1], 1)
qc2.cx(0, 1)
qc2.ry(weights2[0], 0)
qc2.ry(weights2[1], 1)
qc2.cx(0, 1)
qc2.ry(weights2[2], 0)
qc2.ry(weights2[3], 1)
qc2.draw(output="mpl")
input parameters: ['input[0]', 'input[1]']
weight parameters: ['weight[0]', 'weight[1]', 'weight[2]', 'weight[3]']
[29]:
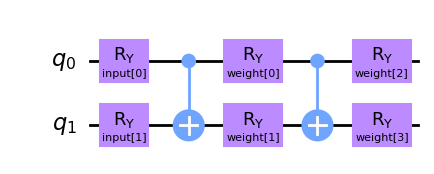
De manera similar a EstimatorQNN, debemos especificar entradas y pesos al instanciar SamplerQNN. En este caso, los argumentos de palabra clave serán: - sampler: instancia primitiva opcional - input_params: lista de parámetros del circuito cuántico que deben tratarse como «entradas de red» - weight_params: lista de parámetros del circuito cuántico que deben tratarse como «pesos de red»
Ten en cuenta que, una vez más, estamos eligiendo no configurar la instancia de Sampler en la QNN y confiando en el valor predeterminado.
[30]:
from qiskit_machine_learning.neural_networks import SamplerQNN
sampler_qnn = SamplerQNN(circuit=qc2, input_params=inputs2, weight_params=weights2)
sampler_qnn
[30]:
<qiskit_machine_learning.neural_networks.sampler_qnn.SamplerQNN at 0x7fd659264880>
Además de los argumentos básicos que se muestran arriba, la SamplerQNN acepta tres configuraciones más: input_gradients, interpret, y output_shape. Estos se introducirán en las secciones 4 y 5.
3. Cómo Ejecutar un Paso hacia Adelante#
3.1. Configuración#
En un entorno real, las entradas estarían definidas por el conjunto de datos y los pesos estarían definidos por el algoritmo de entrenamiento o como parte de un modelo preentrenado. Sin embargo, por el bien de este tutorial, especificaremos conjuntos aleatorios de entrada y pesos de la dimensión correcta:
3.1.1. Ejemplo de EstimatorQNN#
[31]:
estimator_qnn_input = algorithm_globals.random.random(estimator_qnn.num_inputs)
estimator_qnn_weights = algorithm_globals.random.random(estimator_qnn.num_weights)
[32]:
print(
f"Number of input features for EstimatorQNN: {estimator_qnn.num_inputs} \nInput: {estimator_qnn_input}"
)
print(
f"Number of trainable weights for EstimatorQNN: {estimator_qnn.num_weights} \nWeights: {estimator_qnn_weights}"
)
Number of input features for EstimatorQNN: 1
Input: [0.77395605]
Number of trainable weights for EstimatorQNN: 1
Weights: [0.43887844]
3.1.2. Ejemplo de SamplerQNN#
[33]:
sampler_qnn_input = algorithm_globals.random.random(sampler_qnn.num_inputs)
sampler_qnn_weights = algorithm_globals.random.random(sampler_qnn.num_weights)
[34]:
print(
f"Number of input features for SamplerQNN: {sampler_qnn.num_inputs} \nInput: {sampler_qnn_input}"
)
print(
f"Number of trainable weights for SamplerQNN: {sampler_qnn.num_weights} \nWeights: {sampler_qnn_weights}"
)
Number of input features for SamplerQNN: 2
Input: [0.85859792 0.69736803]
Number of trainable weights for SamplerQNN: 4
Weights: [0.09417735 0.97562235 0.7611397 0.78606431]
Una vez que tengamos las entradas y los pesos, veamos los resultados para pases por lotes y sin lotes.
3.2. Paso hacia Adelante Sin Lotes#
3.2.1. Ejemplo de EstimatorQNN#
Para la EstimatorQNN, la forma de salida esperada para el paso hacia adelante es (1, num_qubits * num_observables) donde 1 en nuestro caso es el número de muestras:
[35]:
estimator_qnn_forward = estimator_qnn.forward(estimator_qnn_input, estimator_qnn_weights)
print(
f"Forward pass result for EstimatorQNN: {estimator_qnn_forward}. \nShape: {estimator_qnn_forward.shape}"
)
Forward pass result for EstimatorQNN: [[0.2970094]].
Shape: (1, 1)
3.2.2. Ejemplo de SamplerQNN#
Para la SamplerQNN (sin una función de interpretación personalizada), la forma de salida esperada para el paso hacia adelante es (1, 2**num_qubits). Con una función de interpretación personalizada, la forma de salida será (1, output_shape), donde 1 en nuestro caso es el número de muestras:
[36]:
sampler_qnn_forward = sampler_qnn.forward(sampler_qnn_input, sampler_qnn_weights)
print(
f"Forward pass result for SamplerQNN: {sampler_qnn_forward}. \nShape: {sampler_qnn_forward.shape}"
)
Forward pass result for SamplerQNN: [[0.01826527 0.25735654 0.5267981 0.19758009]].
Shape: (1, 4)
3.3. Paso hacia Adelante Con Lotes#
3.3.1. Ejemplo de EstimatorQNN#
Para el EstimatorQNN, la forma de salida esperada para el paso hacia adelante es (batch_size, num_qubits * num_observables):
[37]:
estimator_qnn_forward_batched = estimator_qnn.forward(
[estimator_qnn_input, estimator_qnn_input], estimator_qnn_weights
)
print(
f"Forward pass result for EstimatorQNN: {estimator_qnn_forward_batched}. \nShape: {estimator_qnn_forward_batched.shape}"
)
Forward pass result for EstimatorQNN: [[0.2970094]
[0.2970094]].
Shape: (2, 1)
3.3.2. Ejemplo de SamplerQNN#
Para la SamplerQNN (sin la función de interpretación personalizada), la forma de salida esperada para el paso hacia adelante es (batch_size, 2**num_qubits). Con una función de interpretación personalizada, la forma de salida será (batch_size, output_shape).
[38]:
sampler_qnn_forward_batched = sampler_qnn.forward(
[sampler_qnn_input, sampler_qnn_input], sampler_qnn_weights
)
print(
f"Forward pass result for SamplerQNN: {sampler_qnn_forward_batched}. \nShape: {sampler_qnn_forward_batched.shape}"
)
Forward pass result for SamplerQNN: [[0.01826527 0.25735654 0.5267981 0.19758009]
[0.01826527 0.25735654 0.5267981 0.19758009]].
Shape: (2, 4)
4. Cómo Ejecutar un Paso hacia Atrás#
Aprovechemos las entradas y los pesos definidos anteriormente para mostrar cómo funciona el paso hacia atrás. Este paso devuelve una tupla (input_gradients, weight_gradients). De forma predeterminada, el paso hacia atrás solo calculará gradientes con respecto a los parámetros de peso.
Si deseas habilitar gradientes con respecto a los parámetros de entrada, debes configurar el siguiente indicador durante la instanciación de la QNN:
qnn = ...QNN(..., input_gradients=True)
Recuerda que los gradientes de entrada son requeridos para el uso de TorchConnector para la integración de PyTorch.
4.1. Paso hacia Atrás sin Gradientes de Entrada#
4.1.1. Ejemplo de EstimatorQNN#
Para EstimatorQNN, la forma de salida esperada para los gradientes de peso es (batch_size, num_qubits * num_observables, num_weights):
[39]:
estimator_qnn_input_grad, estimator_qnn_weight_grad = estimator_qnn.backward(
estimator_qnn_input, estimator_qnn_weights
)
print(
f"Input gradients for EstimatorQNN: {estimator_qnn_input_grad}. \nShape: {estimator_qnn_input_grad}"
)
print(
f"Weight gradients for EstimatorQNN: {estimator_qnn_weight_grad}. \nShape: {estimator_qnn_weight_grad.shape}"
)
Input gradients for EstimatorQNN: None.
Shape: None
Weight gradients for EstimatorQNN: [[[0.63272767]]].
Shape: (1, 1, 1)
4.1.2. Ejemplo de SamplerQNN#
Para la SamplerQNN (sin la función de interpretación personalizada), la forma de salida esperada para el paso hacia adelante es (batch_size, 2**num_qubits, num_weights). Con una función de interpretación personalizada, la forma de salida será (batch_size, output_shape, num_weights).:
[40]:
sampler_qnn_input_grad, sampler_qnn_weight_grad = sampler_qnn.backward(
sampler_qnn_input, sampler_qnn_weights
)
print(
f"Input gradients for SamplerQNN: {sampler_qnn_input_grad}. \nShape: {sampler_qnn_input_grad}"
)
print(
f"Weight gradients for SamplerQNN: {sampler_qnn_weight_grad}. \nShape: {sampler_qnn_weight_grad.shape}"
)
Input gradients for SamplerQNN: None.
Shape: None
Weight gradients for SamplerQNN: [[[ 0.00606238 -0.1124595 -0.06856156 -0.09809236]
[ 0.21167414 -0.09069775 0.06856156 -0.22549618]
[-0.48846674 0.32499215 -0.32262178 0.09809236]
[ 0.27073021 -0.12183491 0.32262178 0.22549618]]].
Shape: (1, 4, 4)
4.2. Paso hacia Atrás con Gradientes de Entrada#
Habilitemos input_gradients para mostrar cuáles son los tamaños de salida esperados para esta opción.
[41]:
estimator_qnn.input_gradients = True
sampler_qnn.input_gradients = True
4.2.1. Ejemplo de EstimatorQNN#
Para la EstimatorQNN, la forma de salida esperada para los gradientes de entrada es `(batch_size, num_qubits * num_observables, num_inputs):
[42]:
estimator_qnn_input_grad, estimator_qnn_weight_grad = estimator_qnn.backward(
estimator_qnn_input, estimator_qnn_weights
)
print(
f"Input gradients for EstimatorQNN: {estimator_qnn_input_grad}. \nShape: {estimator_qnn_input_grad.shape}"
)
print(
f"Weight gradients for EstimatorQNN: {estimator_qnn_weight_grad}. \nShape: {estimator_qnn_weight_grad.shape}"
)
Input gradients for EstimatorQNN: [[[0.3038852]]].
Shape: (1, 1, 1)
Weight gradients for EstimatorQNN: [[[0.63272767]]].
Shape: (1, 1, 1)
4.2.2. Ejemplo de SamplerQNN#
Para la SamplerQNN (sin función de interpretación personalizada), la forma de salida esperada para los gradientes de entrada es (batch_size, 2**num_qubits, num_inputs). Con una función de interpretación personalizada, la forma de salida será (batch_size, output_shape, num_inputs).
[43]:
sampler_qnn_input_grad, sampler_qnn_weight_grad = sampler_qnn.backward(
sampler_qnn_input, sampler_qnn_weights
)
print(
f"Input gradients for SamplerQNN: {sampler_qnn_input_grad}. \nShape: {sampler_qnn_input_grad.shape}"
)
print(
f"Weight gradients for SamplerQNN: {sampler_qnn_weight_grad}. \nShape: {sampler_qnn_weight_grad.shape}"
)
Input gradients for SamplerQNN: [[[-0.05844702 -0.10621091]
[ 0.38798796 -0.19544083]
[-0.34561132 0.09459601]
[ 0.01607038 0.20705573]]].
Shape: (1, 4, 2)
Weight gradients for SamplerQNN: [[[ 0.00606238 -0.1124595 -0.06856156 -0.09809236]
[ 0.21167414 -0.09069775 0.06856156 -0.22549618]
[-0.48846674 0.32499215 -0.32262178 0.09809236]
[ 0.27073021 -0.12183491 0.32262178 0.22549618]]].
Shape: (1, 4, 4)
5. Funcionalidad Avanzada#
5.1. EstimatorQNN con Múltiples Observables#
La EstimatorQNN permite pasar listas de observables para arquitecturas QNN más complejas. Por ejemplo (ten en cuenta el cambio en la forma de salida):
[44]:
observable2 = SparsePauliOp.from_list([("Z" * qc1.num_qubits, 1)])
estimator_qnn2 = EstimatorQNN(
circuit=qc1,
observables=[observable1, observable2],
input_params=[params1[0]],
weight_params=[params1[1]],
)
[45]:
estimator_qnn_forward2 = estimator_qnn2.forward(estimator_qnn_input, estimator_qnn_weights)
estimator_qnn_input_grad2, estimator_qnn_weight_grad2 = estimator_qnn2.backward(
estimator_qnn_input, estimator_qnn_weights
)
print(f"Forward output for EstimatorQNN1: {estimator_qnn_forward.shape}")
print(f"Forward output for EstimatorQNN2: {estimator_qnn_forward2.shape}")
print(f"Backward output for EstimatorQNN1: {estimator_qnn_weight_grad.shape}")
print(f"Backward output for EstimatorQNN2: {estimator_qnn_weight_grad2.shape}")
Forward output for EstimatorQNN1: (1, 1)
Forward output for EstimatorQNN2: (1, 2)
Backward output for EstimatorQNN1: (1, 1, 1)
Backward output for EstimatorQNN2: (1, 2, 1)
5.2. SamplerQNN con interpret personalizado#
Un método interpret común para SamplerQNN es la función parity, que le permite realizar una clasificación binaria. Como se explicó en la sección de creación de instancias, el uso de funciones de interpretación modificará la forma de salida de los pasos hacia adelante y hacia atrás. En el caso de la función de interpretación de paridad, output_shape se fija en 2. Por lo tanto, las formas esperadas del gradiente de peso y gradiente hacia adelante son (batch_size, 2) y (batch_size, 2, num_weights), respectivamente:
[46]:
parity = lambda x: "{:b}".format(x).count("1") % 2
output_shape = 2 # parity = 0, 1
sampler_qnn2 = SamplerQNN(
circuit=qc2,
input_params=inputs2,
weight_params=weights2,
interpret=parity,
output_shape=output_shape,
)
[47]:
sampler_qnn_forward2 = sampler_qnn2.forward(sampler_qnn_input, sampler_qnn_weights)
sampler_qnn_input_grad2, sampler_qnn_weight_grad2 = sampler_qnn2.backward(
sampler_qnn_input, sampler_qnn_weights
)
print(f"Forward output for SamplerQNN1: {sampler_qnn_forward.shape}")
print(f"Forward output for SamplerQNN2: {sampler_qnn_forward2.shape}")
print(f"Backward output for SamplerQNN1: {sampler_qnn_weight_grad.shape}")
print(f"Backward output for SamplerQNN2: {sampler_qnn_weight_grad2.shape}")
Forward output for SamplerQNN1: (1, 4)
Forward output for SamplerQNN2: (1, 2)
Backward output for SamplerQNN1: (1, 4, 4)
Backward output for SamplerQNN2: (1, 2, 4)
6. Conclusión#
En este tutorial, presentamos las dos clases de redes neuronales proporcionadas por qiskit-machine-learning, es decir, EstimatorQNN y SamplerQNN, que amplían la clase base NeuralNetwork. Brindamos algunos antecedentes teóricos, los pasos clave para la inicialización de QNN, el uso básico en pasos hacia adelante y hacia atrás y funcionalidad avanzada.
Ahora te alentamos a que juegues con la configuración del problema y veas cómo los diferentes tamaños de circuito, la entrada y las longitudes de los parámetros de peso influyen en las formas de salida.
[48]:
import qiskit.tools.jupyter
%qiskit_version_table
%qiskit_copyright
Version Information
| Qiskit Software | Version |
|---|---|
qiskit-terra | 0.22.3 |
qiskit-machine-learning | 0.6.0 |
| System information | |
| Python version | 3.9.15 |
| Python compiler | Clang 14.0.6 |
| Python build | main, Nov 24 2022 08:29:02 |
| OS | Darwin |
| CPUs | 8 |
| Memory (Gb) | 64.0 |
| Mon Jan 23 11:57:49 2023 CET | |
This code is a part of Qiskit
© Copyright IBM 2017, 2023.
This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.