Nota
Esta página fue generada a partir de docs/tutorials/03_quantum_kernel.ipynb.
Machine Learning con Kernel Cuántico#
Descripción General#
La tarea general del machine learning es encontrar y estudiar patrones en los datos. Para muchos conjuntos de datos, los puntos de datos se comprenden mejor en un espacio de características de mayor dimensión. Este es el principio fundamental detrás de una serie de algoritmos de machine learning conocidos como métodos de kernel.
En este cuaderno, aprenderás a definir kernels cuánticos utilizando qiskit-machine-learning y cómo estos pueden conectarse a diferentes algoritmos para resolver problemas de clasificación y agrupación (clustering).
Todos los ejemplos utilizados en este tutorial se basan en este artículo de referencia: Supervised learning with quantum enhanced feature spaces.
El contenido está estructurado de la siguiente manera:
Análisis de los Componentes Principales del Kernel
1. Introducción#
1.1. Métodos de Kernel para Machine Learning#
Los métodos de kernel son una colección de algoritmos de análisis de patrones que utilizan funciones de kernel para operar en un espacio de características de alta dimensión. La aplicación más conocida de los métodos de kernel se encuentra en Soporte de Máquinas de Vectores (Support Vector Machines, SVM), algoritmos de aprendizaje supervisado comúnmente utilizados para tareas de clasificación. El objetivo principal de las SVM es encontrar límites de decisión para separar un conjunto dado de puntos de datos en clases. Cuando estos espacios de datos no son linealmente separables, las SVM pueden beneficiarse del uso de kernels para encontrar estos límites.
Formalmente, los límites de decisión son hiperplanos en un espacio de alta dimensionalidad. La función de kernel mapea implícitamente los datos de entrada en este espacio dimensional superior, donde puede ser más fácil resolver el problema inicial. En otras palabras, los kernels pueden permitir que las distribuciones de datos que originalmente no eran separables linealmente se conviertan en un problema separable linealmente. Este es un efecto conocido como el «truco del kernel».
También hay casos de uso para algoritmos no supervisados basados en kernel, por ejemplo, en el contexto de la agrupación (clustering). La Agrupación Espectral es una técnica en la que los puntos de datos se tratan como nodos de un grafo y la tarea de agrupación en clústeres se ve como un problema de partición de grafos en el que los nodos se asignan a un espacio en el que se pueden segregar fácilmente para formar grupos.
1.2. Funciones de Kernel#
Matemáticamente, las funciones de kernel siguen:
\(k(\vec{x}_i, \vec{x}_j) = \langle f(\vec{x}_i), f(\vec{x}_j) \rangle\)
donde * \(k\) es la función de kernel * \(\vec{x}_i, \vec{x}_j\) son entradas \(n\) dimensionales * \(f\) es un mapa del espacio \(n\)-dimensional al espacio \(m\)-dimensional y * \(\langle a,b \rangle\) denota el producto interno
Al considerar datos finitos, una función de kernel se puede representar como una matriz:
\(K_{ij} = k(\vec{x}_i,\vec{x}_j)\).
1.3. Kernels Cuánticos#
La idea principal detrás del machine learning de kernel cuántico es aprovechar los mapas de características cuánticos para realizar el truco del kernel. En este caso, el kernel cuántico se crea asignando un vector de características clásico \(\vec{x}\) a un espacio de Hilbert usando un mapa de características cuánticas \(\phi(\vec{x})\). Matemáticamente:
\(K_{ij} = \left| \langle \phi(\vec{x}_i)| \phi(\vec{x}_j) \rangle \right|^{2}\)
donde * \(K_{ij}\) es la matriz del kernel * \(\vec{x}_i, \vec{x}_j\) son entradas \(n\) dimensionales * \(\phi(\vec{x})\) es el mapa de características cuántico * \(\left| \langle a|b \rangle \right|^{2}\) denota la superposición de dos estados cuánticos \(a\) y \(b\)
Los kernels cuánticos se pueden conectar a algoritmos de aprendizaje de kernel clásicos comunes, como SVM o algoritmos de agrupamiento (clustering), como verás en los ejemplos a continuación. También se pueden aprovechar en nuevos métodos de kernel cuánticos como la clase QSVC proporcionada por qiskit-machine-learning que se explora en este tutorial y otros métodos, como se muestra en tutoriales posteriores sobre Pegasos QSVC y Quantum Kernel Training.
Antes de presentar cualquier ejemplo, configuramos la semilla global para garantizar la reproducibilidad:
[1]:
from qiskit_algorithms.utils import algorithm_globals
algorithm_globals.random_seed = 12345
2. Clasificación#
Esta sección ilustra un flujo de trabajo de clasificación de kernel cuántico usando qiskit-machine-learning.
2.1. Definición del conjunto de datos#
Para este ejemplo, usaremos el conjunto de datos ad hoc como se describe en el artículo de referencia.
Podemos definir la dimensión del conjunto de datos y obtener nuestros subconjuntos de entrenamiento y prueba:
[2]:
from qiskit_machine_learning.datasets import ad_hoc_data
adhoc_dimension = 2
train_features, train_labels, test_features, test_labels, adhoc_total = ad_hoc_data(
training_size=20,
test_size=5,
n=adhoc_dimension,
gap=0.3,
plot_data=False,
one_hot=False,
include_sample_total=True,
)
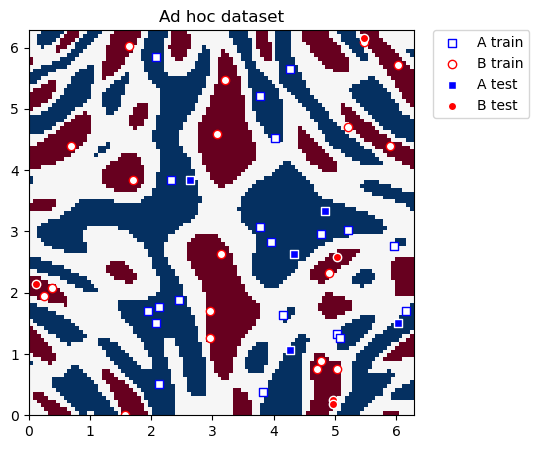
Este conjunto de datos es bidimensional, las dos características están representadas por las coordenadas \(x\) y \(y\), y tiene dos etiquetas de clase: A y B. Podemos graficarlo y ver cómo se ve la distribución. Definimos funciones de utilidad para graficar el conjunto de datos.
[3]:
import matplotlib.pyplot as plt
import numpy as np
def plot_features(ax, features, labels, class_label, marker, face, edge, label):
# A train plot
ax.scatter(
# x coordinate of labels where class is class_label
features[np.where(labels[:] == class_label), 0],
# y coordinate of labels where class is class_label
features[np.where(labels[:] == class_label), 1],
marker=marker,
facecolors=face,
edgecolors=edge,
label=label,
)
def plot_dataset(train_features, train_labels, test_features, test_labels, adhoc_total):
plt.figure(figsize=(5, 5))
plt.ylim(0, 2 * np.pi)
plt.xlim(0, 2 * np.pi)
plt.imshow(
np.asmatrix(adhoc_total).T,
interpolation="nearest",
origin="lower",
cmap="RdBu",
extent=[0, 2 * np.pi, 0, 2 * np.pi],
)
# A train plot
plot_features(plt, train_features, train_labels, 0, "s", "w", "b", "A train")
# B train plot
plot_features(plt, train_features, train_labels, 1, "o", "w", "r", "B train")
# A test plot
plot_features(plt, test_features, test_labels, 0, "s", "b", "w", "A test")
# B test plot
plot_features(plt, test_features, test_labels, 1, "o", "r", "w", "B test")
plt.legend(bbox_to_anchor=(1.05, 1), loc="upper left", borderaxespad=0.0)
plt.title("Ad hoc dataset")
plt.show()
Ahora graficamos el conjunto de datos para la clasificación:
[4]:
plot_dataset(train_features, train_labels, test_features, test_labels, adhoc_total)
2.2. Definición del kernel cuántico#
El siguiente paso es crear una instancia del kernel cuántico que ayude a clasificar estos datos.
Usamos la clase FidelityQuantumKernel, y pasamos dos argumentos de entrada a su constructor:
feature_map: en este caso, un ZZFeatureMap de dos qubits.fidelity: en este caso, la subrutina de fidelidad ComputeUncompute que aprovecha la primitiva Sampler.
NOTA: Si no pasas una instancia Sampler o Fidelity, entonces las instancias de las clases de referencia Sampler y ComputeUncompute (que se encuentran en qiskit.primitives) serán creadas de forma predeterminada.
[5]:
from qiskit.circuit.library import ZZFeatureMap
from qiskit.primitives import Sampler
from qiskit_algorithms.state_fidelities import ComputeUncompute
from qiskit_machine_learning.kernels import FidelityQuantumKernel
adhoc_feature_map = ZZFeatureMap(feature_dimension=adhoc_dimension, reps=2, entanglement="linear")
sampler = Sampler()
fidelity = ComputeUncompute(sampler=sampler)
adhoc_kernel = FidelityQuantumKernel(fidelity=fidelity, feature_map=adhoc_feature_map)
2.3. Clasificación con SVC#
El kernel cuántico ahora se puede conectar a métodos de kernel clásicos, como el algoritmo SVC de scikit-learn. Este algoritmo nos permite definir un kernel personalizado de dos maneras:
proporcionando el kernel como una función invocable
precalculando la matriz del kernel
Kernel como una función invocable#
Definimos un modelo SVC y pasamos directamente la función evaluate del kernel cuántico como un invocable. Una vez que se crea el modelo, lo entrenamos llamando al método fit en el conjunto de datos de entrenamiento y evaluamos la precisión del modelo con score.
[6]:
from sklearn.svm import SVC
adhoc_svc = SVC(kernel=adhoc_kernel.evaluate)
adhoc_svc.fit(train_features, train_labels)
adhoc_score_callable_function = adhoc_svc.score(test_features, test_labels)
print(f"Callable kernel classification test score: {adhoc_score_callable_function}")
Callable kernel classification test score: 1.0
Matriz de kernel precalculada#
En lugar de pasar una función de kernel cuántico como invocable, también podemos calcular previamente las matrices del kernel de entrenamiento y prueba antes de pasarlas al algoritmo SVC de scikit-learn.
Para extraer las matrices de entrenamiento y prueba, podemos llamar a evaluate en el kernel previamente definido y visualizarlas gráficamente de la siguiente manera:
[7]:
adhoc_matrix_train = adhoc_kernel.evaluate(x_vec=train_features)
adhoc_matrix_test = adhoc_kernel.evaluate(x_vec=test_features, y_vec=train_features)
fig, axs = plt.subplots(1, 2, figsize=(10, 5))
axs[0].imshow(
np.asmatrix(adhoc_matrix_train), interpolation="nearest", origin="upper", cmap="Blues"
)
axs[0].set_title("Ad hoc training kernel matrix")
axs[1].imshow(np.asmatrix(adhoc_matrix_test), interpolation="nearest", origin="upper", cmap="Reds")
axs[1].set_title("Ad hoc testing kernel matrix")
plt.show()
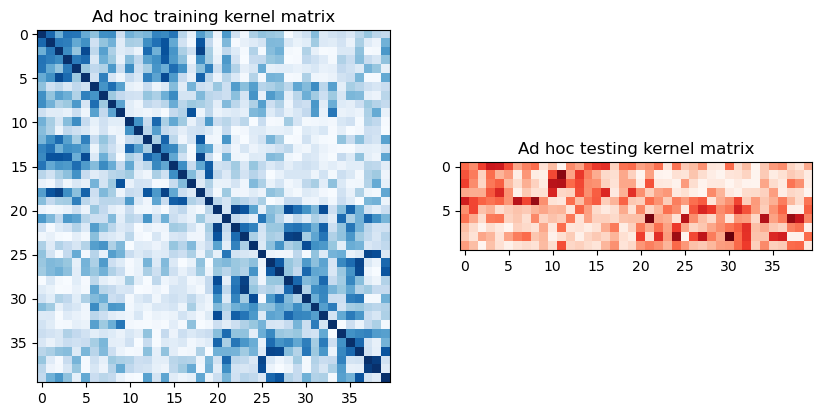
Para usar estas matrices, establecemos el parámetro kernel de una nueva instancia de SVC con "precomputed". Entrenamos al clasificador llamando a fit con la matriz de entrenamiento y el conjunto de datos de entrenamiento. Una vez que se entrena el modelo, lo evaluamos usando la matriz de prueba en el conjunto de datos de prueba.
[8]:
adhoc_svc = SVC(kernel="precomputed")
adhoc_svc.fit(adhoc_matrix_train, train_labels)
adhoc_score_precomputed_kernel = adhoc_svc.score(adhoc_matrix_test, test_labels)
print(f"Precomputed kernel classification test score: {adhoc_score_precomputed_kernel}")
Precomputed kernel classification test score: 1.0
2.4. Clasificación con QSVC#
QSVC es un algoritmo de entrenamiento alternativo proporcionado por qiskit-machine-learning por conveniencia. Es una extensión de SVC que acepta un kernel cuántico en lugar del método kernel.evaluate mostrado anteriormente.
[9]:
from qiskit_machine_learning.algorithms import QSVC
qsvc = QSVC(quantum_kernel=adhoc_kernel)
qsvc.fit(train_features, train_labels)
qsvc_score = qsvc.score(test_features, test_labels)
print(f"QSVC classification test score: {qsvc_score}")
QSVC classification test score: 1.0
2.5. Evaluación de modelos utilizados para la clasificación#
[10]:
print(f"Classification Model | Accuracy Score")
print(f"---------------------------------------------------------")
print(f"SVC using kernel as a callable function | {adhoc_score_callable_function:10.2f}")
print(f"SVC using precomputed kernel matrix | {adhoc_score_precomputed_kernel:10.2f}")
print(f"QSVC | {qsvc_score:10.2f}")
Classification Model | Accuracy Score
---------------------------------------------------------
SVC using kernel as a callable function | 1.00
SVC using precomputed kernel matrix | 1.00
QSVC | 1.00
Como el conjunto de datos de clasificación es pequeño, encontramos que los tres modelos logran una precisión del 100%.
3. Agrupación (Clustering)#
El segundo flujo de trabajo de este tutorial se centra en una tarea de agrupamiento (clustering) utilizando qiskit-machine-learning y el algoritmo de agrupamiento espectral de scikit-learn.
3.1. Definición del conjunto de datos#
Una vez más usaremos el conjunto de datos ad hoc, pero ahora generado con una brecha mayor de 0.6 (ejemplo anterior: 0.3) entre las dos clases.
Ten en cuenta que la agrupación en clústeres se incluye en la categoría de machine learning no supervisado, por lo que no se requiere un conjunto de datos de prueba.
[11]:
adhoc_dimension = 2
train_features, train_labels, test_features, test_labels, adhoc_total = ad_hoc_data(
training_size=25,
test_size=0,
n=adhoc_dimension,
gap=0.6,
plot_data=False,
one_hot=False,
include_sample_total=True,
)
Graficamos el conjunto de datos de agrupamiento a continuación:
[12]:
plt.figure(figsize=(5, 5))
plt.ylim(0, 2 * np.pi)
plt.xlim(0, 2 * np.pi)
plt.imshow(
np.asmatrix(adhoc_total).T,
interpolation="nearest",
origin="lower",
cmap="RdBu",
extent=[0, 2 * np.pi, 0, 2 * np.pi],
)
# A label plot
plot_features(plt, train_features, train_labels, 0, "s", "w", "b", "B")
# B label plot
plot_features(plt, train_features, train_labels, 1, "o", "w", "r", "B")
plt.legend(bbox_to_anchor=(1.05, 1), loc="upper left", borderaxespad=0.0)
plt.title("Ad hoc dataset for clustering")
plt.show()
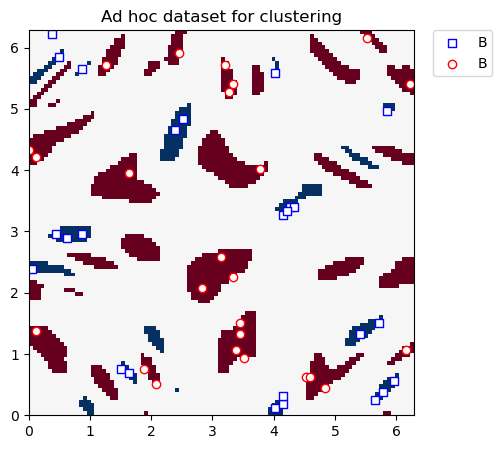
3.2. Definición del Kernel Cuántico#
Usamos una configuración idéntica a la del ejemplo de clasificación. Creamos otra instancia de la clase FidelityQuantumKernel con un ZZFeatureMap, pero puedes notar que en este caso no proporcionamos una instancia de fidelity. Esto se debe a que el método ComputeUncompute proporcionado en el caso anterior es instanciado de forma predeterminada cuando la instancia de fidelidad no se proporciona explícitamente.
[13]:
adhoc_feature_map = ZZFeatureMap(feature_dimension=adhoc_dimension, reps=2, entanglement="linear")
adhoc_kernel = FidelityQuantumKernel(feature_map=adhoc_feature_map)
3.3. Agrupamiento (Clustering) con el Modelo de Agrupamiento Espectral#
El algoritmo de agrupamiento espectral de scikit-learn nos permite definir un kernel personalizado de dos maneras (al igual que SVC):
proporcionando el kernel como una función invocable
precalculando la matriz del kernel.
Con la clase FidelityQuantumKernel actual en qiskit-machine-learning, solo podemos usar la última opción, por lo que precalculamos la matriz del kernel llamando a evaluate y la visualizamos de la siguiente manera:
[14]:
adhoc_matrix = adhoc_kernel.evaluate(x_vec=train_features)
plt.figure(figsize=(5, 5))
plt.imshow(np.asmatrix(adhoc_matrix), interpolation="nearest", origin="upper", cmap="Greens")
plt.title("Ad hoc clustering kernel matrix")
plt.show()
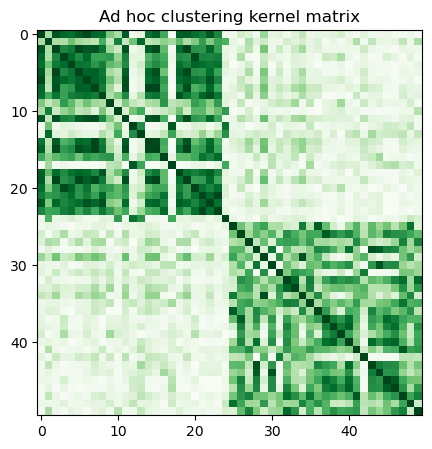
A continuación, definimos un modelo de agrupamiento espectral y lo ajustamos utilizando el kernel precalculado. Además, calificamos las etiquetas utilizando información mutua normalizada, ya que conocemos las etiquetas de clase a priori (de antemano).
[15]:
from sklearn.cluster import SpectralClustering
from sklearn.metrics import normalized_mutual_info_score
adhoc_spectral = SpectralClustering(2, affinity="precomputed")
cluster_labels = adhoc_spectral.fit_predict(adhoc_matrix)
cluster_score = normalized_mutual_info_score(cluster_labels, train_labels)
print(f"Clustering score: {cluster_score}")
Clustering score: 0.7287008798015754
4. Análisis de Componentes Principales del Kernel#
Esta sección se centra en una tarea de análisis de componentes principales utilizando un algoritmo PCA de kernel. Calculamos una matriz del kernel usando un ZZFeatureMap y mostramos que este enfoque traduce las características originales a un nuevo espacio, donde los ejes se eligen a lo largo de los componentes principales. En este espacio, la tarea de clasificación se puede realizar con un modelo más simple en lugar de una SVM.
4.1. Definición del conjunto de datos#
Nuevamente, usamos el conjunto de datos ad hoc con una brecha de 0.6 entre las dos clases. Este conjunto de datos se asemeja al conjunto de datos que teníamos en la sección de agrupamiento, la diferencia es que en este caso test_size no es cero.
[16]:
adhoc_dimension = 2
train_features, train_labels, test_features, test_labels, adhoc_total = ad_hoc_data(
training_size=25,
test_size=10,
n=adhoc_dimension,
gap=0.6,
plot_data=False,
one_hot=False,
include_sample_total=True,
)
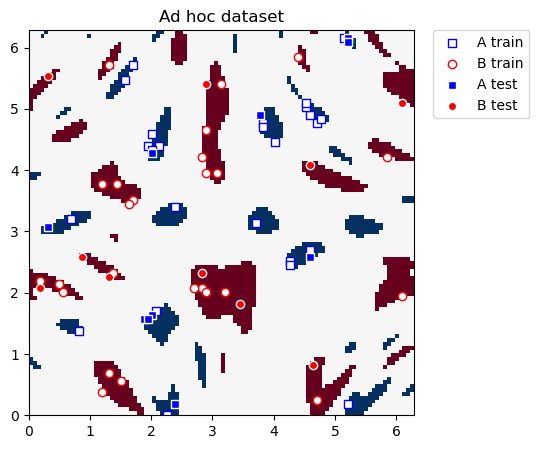
Graficamos los conjuntos de datos de entrenamiento y prueba a continuación. Nuestro objetivo final en esta sección es construir nuevas coordenadas donde las dos clases se puedan separar linealmente.
[17]:
plot_dataset(train_features, train_labels, test_features, test_labels, adhoc_total)
4.2. Definición del Kernel Cuántico#
Procedemos con la misma configuración del kernel que en la tarea de clasificación, es decir, un circuito ZZFeatureMap como un mapa de características y una instancia de FidelityQuantumKernel.
[18]:
feature_map = ZZFeatureMap(feature_dimension=2, reps=2, entanglement="linear")
qpca_kernel = FidelityQuantumKernel(fidelity=fidelity, feature_map=feature_map)
Luego, evaluamos las matrices del kernel para las características de entrenamiento y prueba.
[19]:
matrix_train = qpca_kernel.evaluate(x_vec=train_features)
matrix_test = qpca_kernel.evaluate(x_vec=test_features, y_vec=train_features)
4.3. Comparación del Kernel PCA con kernel gaussiano y cuántico#
En esta sección usamos la implementación KernelPCA de scikit-learn, con el parámetro kernel establecido en «rbf» para un kernel gaussiano y «precalculado» para un kernel cuántico. El primero es muy popular en los modelos clásicos de machine learning, mientras que el segundo permite usar un kernel cuántico definido como qpca_kernel.
Se puede observar que el modelo Kernel PCA basado en el kernel gaussiano no logra que el conjunto de datos sea linealmente separable, mientras que el kernel cuántico sí lo logra.
Si bien PCA generalmente se usa para reducir la cantidad de características en un conjunto de datos o, en otras palabras, para reducir la dimensionalidad de un conjunto de datos, no lo hacemos aquí. Más bien, mantenemos el número de dimensiones y empleamos el kernel PCA, principalmente con fines de visualización, para mostrar que la clasificación en el conjunto de datos transformado se vuelve fácilmente tratable mediante métodos lineales, como la regresión logística. Usamos este método para separar dos clases en el espacio de componentes principales con un modelo LogisticRegression de scikit-learn. Como de costumbre, lo entrenamos llamando al método fit en el conjunto de datos de entrenamiento y evaluamos la precisión del modelo con score.
[20]:
from sklearn.decomposition import KernelPCA
kernel_pca_rbf = KernelPCA(n_components=2, kernel="rbf")
kernel_pca_rbf.fit(train_features)
train_features_rbf = kernel_pca_rbf.transform(train_features)
test_features_rbf = kernel_pca_rbf.transform(test_features)
kernel_pca_q = KernelPCA(n_components=2, kernel="precomputed")
train_features_q = kernel_pca_q.fit_transform(matrix_train)
test_features_q = kernel_pca_q.transform(matrix_test)
Aquí entrenamos y puntuamos un modelo.
[21]:
from sklearn.linear_model import LogisticRegression
logistic_regression = LogisticRegression()
logistic_regression.fit(train_features_q, train_labels)
logistic_score = logistic_regression.score(test_features_q, test_labels)
print(f"Logistic regression score: {logistic_score}")
Logistic regression score: 0.9
Grafiquemos los resultados. Primero, graficamos el conjunto de datos transformados que obtenemos con el kernel cuántico. En la misma gráfica también agregamos los resultados del modelo. Luego, graficamos el conjunto de datos transformados que obtenemos con el kernel gaussiano.
[22]:
fig, (q_ax, rbf_ax) = plt.subplots(1, 2, figsize=(10, 5))
plot_features(q_ax, train_features_q, train_labels, 0, "s", "w", "b", "A train")
plot_features(q_ax, train_features_q, train_labels, 1, "o", "w", "r", "B train")
plot_features(q_ax, test_features_q, test_labels, 0, "s", "b", "w", "A test")
plot_features(q_ax, test_features_q, test_labels, 1, "o", "r", "w", "A test")
q_ax.set_ylabel("Principal component #1")
q_ax.set_xlabel("Principal component #0")
q_ax.set_title("Projection of training and test data\n using KPCA with Quantum Kernel")
# Plotting the linear separation
h = 0.01 # step size in the mesh
# create a mesh to plot in
x_min, x_max = train_features_q[:, 0].min() - 1, train_features_q[:, 0].max() + 1
y_min, y_max = train_features_q[:, 1].min() - 1, train_features_q[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
predictions = logistic_regression.predict(np.c_[xx.ravel(), yy.ravel()])
# Put the result into a color plot
predictions = predictions.reshape(xx.shape)
q_ax.contourf(xx, yy, predictions, cmap=plt.cm.RdBu, alpha=0.2)
plot_features(rbf_ax, train_features_rbf, train_labels, 0, "s", "w", "b", "A train")
plot_features(rbf_ax, train_features_rbf, train_labels, 1, "o", "w", "r", "B train")
plot_features(rbf_ax, test_features_rbf, test_labels, 0, "s", "b", "w", "A test")
plot_features(rbf_ax, test_features_rbf, test_labels, 1, "o", "r", "w", "A test")
rbf_ax.set_ylabel("Principal component #1")
rbf_ax.set_xlabel("Principal component #0")
rbf_ax.set_title("Projection of training data\n using KernelPCA")
plt.show()
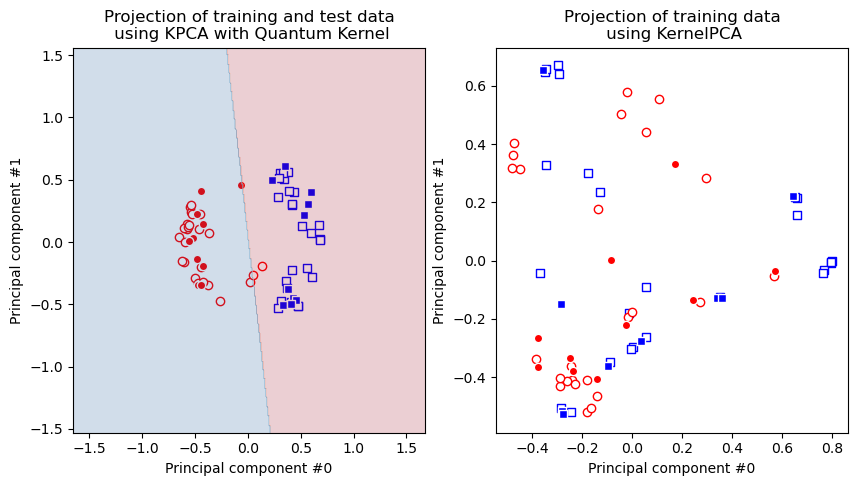
Como podemos ver, los puntos de datos en la figura de la derecha no son separables, pero están en la figura de la izquierda, por lo tanto, en el caso del kernel cuántico, podemos aplicar modelos lineales en el conjunto de datos transformado y es por eso que el clasificador SVM funciona perfectamente bien en el conjunto de datos ad hoc como vimos en la sección de clasificación.
5. Conclusión#
En este tutorial:
Revisamos los fundamentos del aprendizaje del kernel cuántico
Entendimos cómo definir kernels cuánticos como instancias de
FidelityQuantumKernelAprendimos a usar el algoritmo
SVCdescikit-learncon un kernel cuántico personalizado como una función invocable frente a una matriz de kernel cuántico precalculada para la clasificaciónAprendimos a entrenar clasificadores con el algoritmo
QSVCdeqiskit-machine-learningAprendimos a usar los algoritmos
SpectralClusteringdescikit-learncon una matriz de kernel cuántico precalculada para la agrupación (clustering)Investigamos cómo conectar un kernel cuántico en el algoritmo
KernelPCAdescikit-learny transformar el conjunto de datos ad-hoc en uno nuevo que pueda ser abordado por un modelo lineal.
Para mayor referencia, scikit-learn tiene otros algoritmos que pueden usar una matriz de kernel precalculada, como:
[23]:
import qiskit.tools.jupyter
%qiskit_version_table
%qiskit_copyright
Version Information
| Qiskit Software | Version |
|---|---|
qiskit-terra | 0.23.1 |
qiskit-aer | 0.11.2 |
qiskit-ibmq-provider | 0.20.0 |
qiskit | 0.41.0 |
qiskit-machine-learning | 0.5.0 |
| System information | |
| Python version | 3.10.9 |
| Python compiler | GCC 11.2.0 |
| Python build | main, Jan 11 2023 15:21:40 |
| OS | Linux |
| CPUs | 10 |
| Memory (Gb) | 7.394691467285156 |
| Wed Feb 22 10:36:16 2023 CET | |
This code is a part of Qiskit
© Copyright IBM 2017, 2023.
This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.