Nota
Esta página fue generada a partir de docs/tutorials/02a_training_a_quantum_model_on_a_real_dataset.ipynb.
Entrenamiento de un Modelo Cuántico en un Conjunto de Datos Real#
Este tutorial demostrará cómo entrenar un modelo de machine learning cuántico para abordar un problema de clasificación. Los tutoriales anteriores han presentado pequeños conjuntos de datos artificiales. Aquí aumentaremos la complejidad del problema al considerar un conjunto de datos clásico de la vida real. Decidimos elegir un problema muy conocido, aunque todavía relativamente pequeño: el conjunto de datos de la flor Iris. Este conjunto de datos incluso tiene su propia página de Wikipedia. Aunque el conjunto de datos de Iris es bien conocido por los científicos de datos, lo presentaremos brevemente para refrescarnos la memoria. A modo de comparación, primero entrenaremos una contraparte clásica del modelo cuántico.
Entonces, empecemos:
Primero, cargaremos el conjunto de datos y exploraremos cómo se ve.
A continuación, entrenaremos un modelo clásico usando SVC de scikit-learn para ver qué tan bien se puede resolver el problema de clasificación usando métodos clásicos.
Después de eso, presentaremos el Clasificador Cuántico Variacional (Variational Quantum Classifier, VQC).
Para concluir, compararemos los resultados obtenidos con ambos modelos.
1. Análisis de Datos Exploratorios#
Primero, exploremos el conjunto de datos de Iris que usarás este tutorial y veamos qué contiene. Para nuestra comodidad, este conjunto de datos está disponible en scikit-learn y se puede cargar fácilmente.
[2]:
from sklearn.datasets import load_iris
iris_data = load_iris()
Si no se especifican parámetros en la función load_iris, scikit-learn devuelve un objeto similar a un diccionario. Imprimamos la descripción del conjunto de datos y veamos qué hay dentro.
[3]:
print(iris_data.DESCR)
.. _iris_dataset:
Iris plants dataset
--------------------
**Data Set Characteristics:**
:Number of Instances: 150 (50 in each of three classes)
:Number of Attributes: 4 numeric, predictive attributes and the class
:Attribute Information:
- sepal length in cm
- sepal width in cm
- petal length in cm
- petal width in cm
- class:
- Iris-Setosa
- Iris-Versicolour
- Iris-Virginica
:Summary Statistics:
============== ==== ==== ======= ===== ====================
Min Max Mean SD Class Correlation
============== ==== ==== ======= ===== ====================
sepal length: 4.3 7.9 5.84 0.83 0.7826
sepal width: 2.0 4.4 3.05 0.43 -0.4194
petal length: 1.0 6.9 3.76 1.76 0.9490 (high!)
petal width: 0.1 2.5 1.20 0.76 0.9565 (high!)
============== ==== ==== ======= ===== ====================
:Missing Attribute Values: None
:Class Distribution: 33.3% for each of 3 classes.
:Creator: R.A. Fisher
:Donor: Michael Marshall (MARSHALL%PLU@io.arc.nasa.gov)
:Date: July, 1988
The famous Iris database, first used by Sir R.A. Fisher. The dataset is taken
from Fisher's paper. Note that it's the same as in R, but not as in the UCI
Machine Learning Repository, which has two wrong data points.
This is perhaps the best known database to be found in the
pattern recognition literature. Fisher's paper is a classic in the field and
is referenced frequently to this day. (See Duda & Hart, for example.) The
data set contains 3 classes of 50 instances each, where each class refers to a
type of iris plant. One class is linearly separable from the other 2; the
latter are NOT linearly separable from each other.
.. topic:: References
- Fisher, R.A. "The use of multiple measurements in taxonomic problems"
Annual Eugenics, 7, Part II, 179-188 (1936); also in "Contributions to
Mathematical Statistics" (John Wiley, NY, 1950).
- Duda, R.O., & Hart, P.E. (1973) Pattern Classification and Scene Analysis.
(Q327.D83) John Wiley & Sons. ISBN 0-471-22361-1. See page 218.
- Dasarathy, B.V. (1980) "Nosing Around the Neighborhood: A New System
Structure and Classification Rule for Recognition in Partially Exposed
Environments". IEEE Transactions on Pattern Analysis and Machine
Intelligence, Vol. PAMI-2, No. 1, 67-71.
- Gates, G.W. (1972) "The Reduced Nearest Neighbor Rule". IEEE Transactions
on Information Theory, May 1972, 431-433.
- See also: 1988 MLC Proceedings, 54-64. Cheeseman et al"s AUTOCLASS II
conceptual clustering system finds 3 classes in the data.
- Many, many more ...
Hay algunas observaciones interesantes que podemos encontrar en esta descripción del conjunto de datos:
Hay 150 muestras (instancias) en el conjunto de datos.
Hay cuatro características (atributos) en cada muestra.
Hay tres etiquetas (clases) en el conjunto de datos.
El conjunto de datos está perfectamente equilibrado, ya que hay el mismo número de muestras (50) en cada clase.
Podemos ver que las características no están normalizadas y sus rangos de valores son diferentes, por ejemplo, \([4.3, 7.9]\) y \([0.1, 2.5]\) para la longitud del sépalo y el ancho del pétalo, respectivamente. Por lo tanto, puede ser útil transformar las características a la misma escala.
Como se indica en la tabla anterior, la correlación de característica a clase en algunos casos es muy alta; esto puede llevarnos a pensar que nuestro modelo debería adaptarse bien al conjunto de datos.
Solo examinamos la descripción del conjunto de datos, pero hay propiedades adicionales disponibles en el objeto iris_data. Ahora vamos a trabajar con características y etiquetas del conjunto de datos.
[4]:
features = iris_data.data
labels = iris_data.target
En primer lugar, normalizaremos las características. Es decir, aplicaremos una transformación simple para representar todas las características en la misma escala. En nuestro caso, comprimimos todas las funciones en el intervalo \([0, 1]\). La normalización es una técnica común en el machine learning y, a menudo, conduce a una mejor estabilidad numérica y convergencia de un algoritmo.
Podemos usar MinMaxScaler de scikit-learn para realizar esto. Sin especificar parámetros, esto hace exactamente lo que se requiere: mapea los datos a \([0, 1]\).
[5]:
from sklearn.preprocessing import MinMaxScaler
features = MinMaxScaler().fit_transform(features)
Veamos cómo se ven nuestros datos. Graficamos las características por pares para ver si hay una correlación observable entre ellas.
[6]:
import pandas as pd
import seaborn as sns
df = pd.DataFrame(iris_data.data, columns=iris_data.feature_names)
df["class"] = pd.Series(iris_data.target)
sns.pairplot(df, hue="class", palette="tab10")
[6]:
<seaborn.axisgrid.PairGrid at 0x1c92dbc4188>
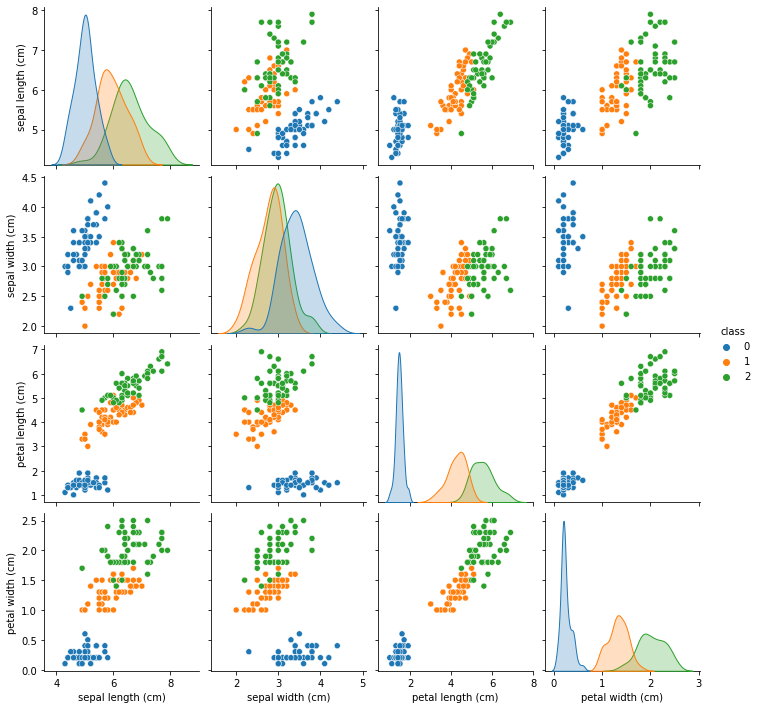
De las gráficas, vemos que la clase 0 es fácilmente separable de las otras dos clases, mientras que las clases 1 y 2 a veces están empalmadas, especialmente con respecto a la característica del «ancho del sépalo».
A continuación, veamos cómo el machine learning clásico maneja este conjunto de datos.
2. Entrenamiento de un Modelo Clásico de Machine Learning#
Antes de entrenar un modelo, debemos dividir el conjunto de datos en dos partes: un conjunto de datos de entrenamiento y un conjunto de datos de prueba. Usaremos el primero para entrenar el modelo y el segundo para verificar qué tan bien funcionan nuestros modelos en datos no vistos.
Como de costumbre, le pediremos a scikit-learn que haga el trabajo aburrido por nosotros. También fijaremos la semilla para garantizar que los resultados sean reproducibles.
[7]:
from sklearn.model_selection import train_test_split
from qiskit_algorithms.utils import algorithm_globals
algorithm_globals.random_seed = 123
train_features, test_features, train_labels, test_labels = train_test_split(
features, labels, train_size=0.8, random_state=algorithm_globals.random_seed
)
Entrenamos un clasificador de vectores de soporte clásico de scikit-learn. En aras de la simplicidad, no modificamos ningún parámetro y confiamos en los valores predeterminados.
[8]:
from sklearn.svm import SVC
svc = SVC()
_ = svc.fit(train_features, train_labels) # suppress printing the return value
Ahora comprobamos qué tan bien funciona nuestro modelo clásico. Analizaremos las puntuaciones en el apartado de conclusiones.
[9]:
train_score_c4 = svc.score(train_features, train_labels)
test_score_c4 = svc.score(test_features, test_labels)
print(f"Classical SVC on the training dataset: {train_score_c4:.2f}")
print(f"Classical SVC on the test dataset: {test_score_c4:.2f}")
Classical SVC on the training dataset: 0.99
Classical SVC on the test dataset: 0.97
Como puede verse en las puntuaciones, el algoritmo SVC clásico funciona muy bien. A continuación, es hora de analizar los modelos de machine learning cuántico.
3. Entrenamiento de un Modelo de Machine Learning Cuántico#
Como ejemplo de un modelo cuántico, entrenaremos un clasificador cuántico variacional (variational quantum classifier, VQC). El VQC es el clasificador más simple disponible en Qiskit Machine Learning y es un buen punto de partida para los recién llegados al machine learning cuántico que tienen experiencia en el machine learning clásico.
Pero antes de entrenar un modelo, examinemos qué comprende la clase VQC. Dos de sus elementos centrales son el mapa de características y el ansatz. Ahora se explicará cuáles son.
Nuestros datos son clásicos, lo que significa que consisten en un conjunto de bits, no de qubits. Necesitamos una forma de codificar los datos como qubits. Este proceso es crucial si queremos obtener un modelo cuántico efectivo. Por lo general, nos referimos a este mapeo como codificación de datos, incrustación de datos o carga de datos, y esta es la función del mapa de características. Si bien el mapeo de características es un mecanismo común de ML, este proceso de carga de datos en estados cuánticos no aparece en el machine learning clásico, ya que solo funciona en el mundo clásico.
Una vez cargados los datos, debemos aplicar inmediatamente un circuito cuántico parametrizado. Este circuito es un análogo directo a las capas en las redes neuronales clásicas. Tiene un conjunto de parámetros o pesos ajustables. Los pesos se optimizan de manera que minimicen una función objetivo. Esta función objetivo caracteriza la distancia entre las predicciones y los datos etiquetados conocidos. Un circuito cuántico parametrizado también se denomina estado de prueba parametrizado, forma variacional o ansatz. Quizás, este último es el término más utilizado.
Para obtener más información, dirigimos al lector al Curso de Machine Learning Cuántico.
Nuestra elección de mapa de características será ZZFeatureMap. El ZZFeatureMap es uno de los mapas de características estándar en la biblioteca de circuitos de Qiskit. Pasamos num_features como feature_dimension, lo que significa que el mapa de características tendrá num_features o 4 qubits.
Descomponemos el mapa de características en sus compuertas constituyentes para darle al lector una idea de cómo pueden verse los mapas de características.
[10]:
from qiskit.circuit.library import ZZFeatureMap
num_features = features.shape[1]
feature_map = ZZFeatureMap(feature_dimension=num_features, reps=1)
feature_map.decompose().draw(output="mpl", fold=20)
[10]:
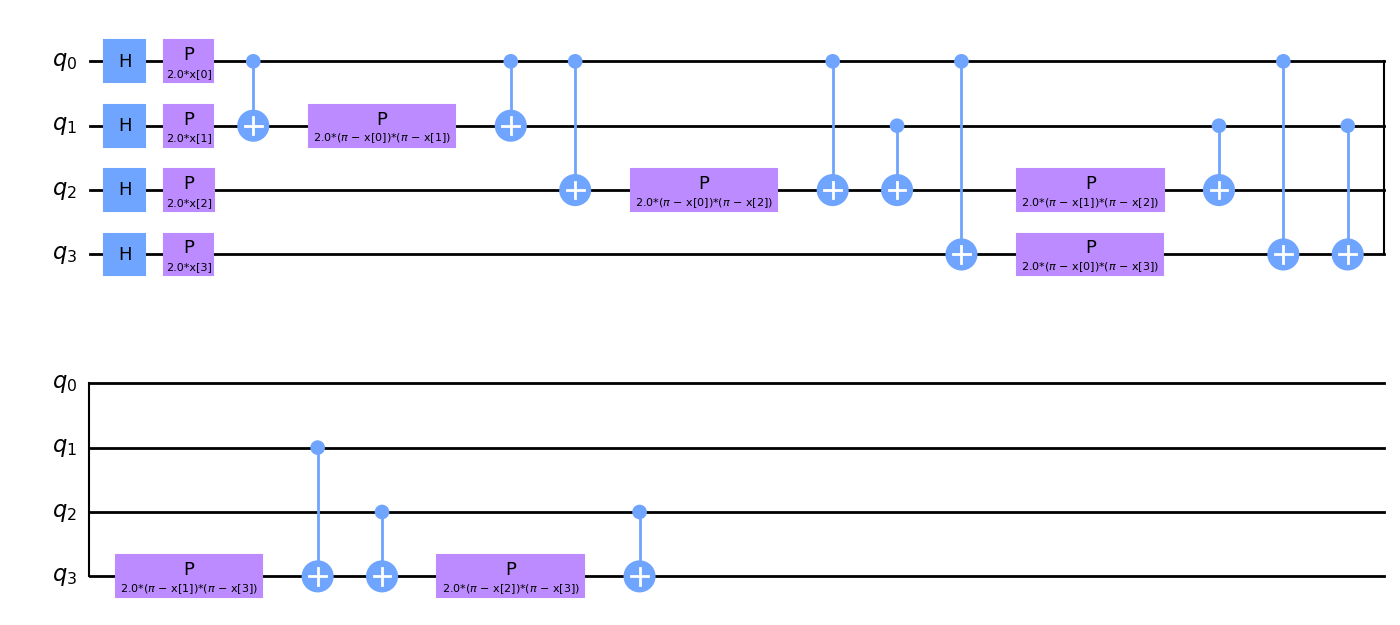
Si observas detenidamente el diagrama del mapa de características, notarás los parámetros x[0], ..., x[3]. Estos son marcadores de posición para nuestras funciones.
Ahora creamos y mostramos nuestro ansatz. Presta atención a la estructura repetitiva del circuito ansatz. Definimos el número de estas repeticiones usando el parámetro reps.
[11]:
from qiskit.circuit.library import RealAmplitudes
ansatz = RealAmplitudes(num_qubits=num_features, reps=3)
ansatz.decompose().draw(output="mpl", fold=20)
[11]:
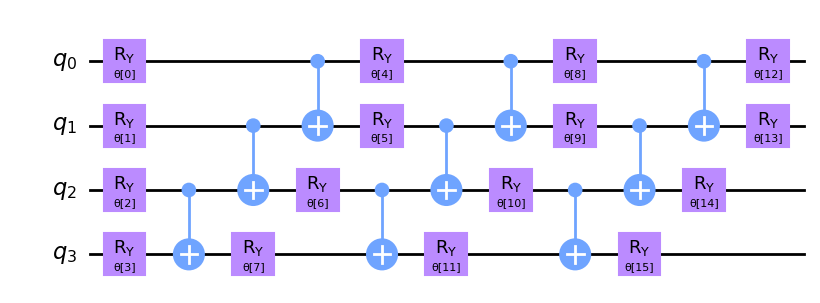
Este circuito tiene 16 parámetros llamados θ[0], ..., θ[15]. Estos son los pesos entrenables del clasificador.
Luego elegimos un algoritmo de optimización para usar en el proceso de entrenamiento. Este paso es similar a lo que puedes encontrar en los frameworks clásicos de deep learning. Para acelerar el proceso de entrenamiento, elegimos un optimizador sin gradiente. Puedes explorar otros optimizadores disponibles en Qiskit.
[12]:
from qiskit_algorithms.optimizers import COBYLA
optimizer = COBYLA(maxiter=100)
En el siguiente paso, definimos dónde entrenar nuestro clasificador. Podemos entrenar en un simulador o en una computadora cuántica real. Aquí, usaremos un simulador. Creamos una instancia de la primitiva Sampler. Esta es la implementación de referencia en la que está basado el vector de estado. Con los servicios de qiskit runtime, puedes crear un sampler que esté respaldado por una computadora cuántica.
[13]:
from qiskit.primitives import Sampler
sampler = Sampler()
Agregaremos una función de devolución de llamada nombrada callback_graph. VQC llamará a esta función para cada evaluación de la función objetivo con dos parámetros: los pesos actuales y el valor de la función objetivo en esos pesos. Nuestra devolución de llamada agregará el valor de la función objetivo a una matriz para que podamos graficar la iteración frente al valor de la función objetivo. La devolución de llamada actualizará la gráfica en cada iteración. Ten en cuenta que puedes hacer lo que quieras dentro de una función de devolución de llamada, siempre que tenga la firma de dos parámetros que mencionamos anteriormente.
[14]:
from matplotlib import pyplot as plt
from IPython.display import clear_output
objective_func_vals = []
plt.rcParams["figure.figsize"] = (12, 6)
def callback_graph(weights, obj_func_eval):
clear_output(wait=True)
objective_func_vals.append(obj_func_eval)
plt.title("Objective function value against iteration")
plt.xlabel("Iteration")
plt.ylabel("Objective function value")
plt.plot(range(len(objective_func_vals)), objective_func_vals)
plt.show()
Ahora estamos listos para construir el clasificador y ajustarlo.
VQC significa «clasificador cuántico variacional» («variational quantum classifier.»). Toma un mapa de características y un ansatz y construye una red neuronal cuántica automáticamente. En el caso más simple, basta con pasar el número de qubits y una quantum instance para construir un clasificador válido. Puedes omitir el parámetro sampler, en este caso se creará una instancia de Sampler de la forma en que la creamos anteriormente. Lo creamos manualmente solo con fines ilustrativos.
El entrenamiento puede tomar algún tiempo. Por favor sé paciente.
[15]:
import time
from qiskit_machine_learning.algorithms.classifiers import VQC
vqc = VQC(
sampler=sampler,
feature_map=feature_map,
ansatz=ansatz,
optimizer=optimizer,
callback=callback_graph,
)
# clear objective value history
objective_func_vals = []
start = time.time()
vqc.fit(train_features, train_labels)
elapsed = time.time() - start
print(f"Training time: {round(elapsed)} seconds")
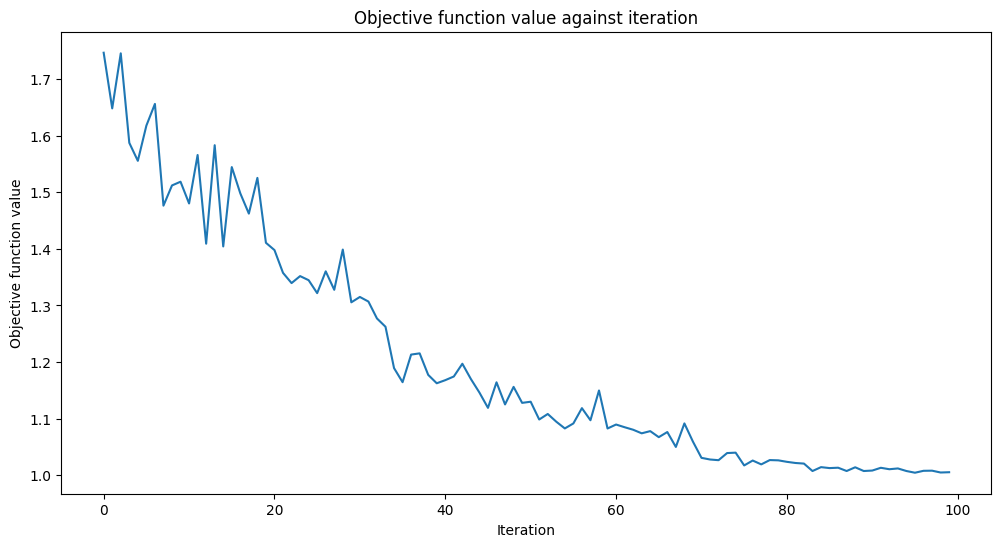
Training time: 303 seconds
Veamos cómo se comporta el modelo cuántico en el conjunto de datos en la vida real.
[16]:
train_score_q4 = vqc.score(train_features, train_labels)
test_score_q4 = vqc.score(test_features, test_labels)
print(f"Quantum VQC on the training dataset: {train_score_q4:.2f}")
print(f"Quantum VQC on the test dataset: {test_score_q4:.2f}")
Quantum VQC on the training dataset: 0.85
Quantum VQC on the test dataset: 0.87
Como podemos ver, las puntuaciones son altas y el modelo se puede usar para predecir etiquetas en datos no vistos.
Ahora veamos qué podemos ajustar para obtener modelos aún mejores.
Los componentes clave son el mapa de características y el ansatz. Puedes ajustar los parámetros. En nuestro caso, puedes cambiar el parámetro
repsque especifica cuántas repeticiones de un patrón de compuertas agregamos al circuito. Los valores más grandes conducen a más operaciones de entrelazamiento y más parámetros. Por lo tanto, el modelo puede ser más flexible, pero la mayor cantidad de parámetros también agrega complejidad, y el entrenamiento de dicho modelo suele llevar más tiempo. Además, podemos terminar sobreajustando el modelo. Puedes probar los otros mapas de características y ansatzes disponibles en la biblioteca de circuitos de Qiskit, o puedes crear circuitos personalizados.Puedes probar otros optimizadores. Qiskit contiene un montón de ellos. Algunos de ellos están libres de gradientes, otros no. Si eliges un optimizador basado en gradiente, por ejemplo,
L_BFGS_B, espera que aumente el tiempo de entrenamiento. Además de la función objetivo, estos optimizadores deben evaluar el gradiente con respecto a los parámetros de entrenamiento, lo que conduce a un mayor número de ejecuciones del circuito por iteración.Otra opción es muestrear aleatoriamente (o de manera determinista) el
initial_pointy ajustar el modelo varias veces.
Pero, ¿qué sucede si un conjunto de datos contiene más características de las que puede manejar una computadora cuántica moderna? Recuerda, en este ejemplo, teníamos la misma cantidad de qubits que la cantidad de características en el conjunto de datos, pero es posible que este no sea siempre el caso.
4. Reducción del Número de Características#
En esta sección, reducimos la cantidad de características en nuestro conjunto de datos y volvemos a entrenar nuestros modelos. Avanzaremos más rápido esta vez, ya que los pasos son los mismos, excepto el primero, donde aplicamos una transformación PCA.
Transformamos nuestras cuatro características en solo dos características. Esta reducción de dimensionalidad es solo para fines educativos. Como viste en la sección anterior, podemos entrenar un modelo cuántico usando las cuatro características del conjunto de datos.
Ahora, podemos graficar fácilmente estas dos características en una sola figura.
[17]:
from sklearn.decomposition import PCA
features = PCA(n_components=2).fit_transform(features)
plt.rcParams["figure.figsize"] = (6, 6)
sns.scatterplot(x=features[:, 0], y=features[:, 1], hue=labels, palette="tab10")
[17]:
<AxesSubplot:>
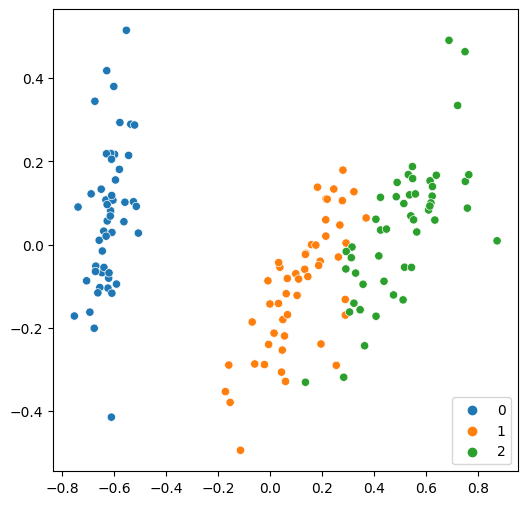
Como de costumbre, primero dividimos el conjunto de datos y luego ajustamos un modelo clásico.
[18]:
train_features, test_features, train_labels, test_labels = train_test_split(
features, labels, train_size=0.8, random_state=algorithm_globals.random_seed
)
svc.fit(train_features, train_labels)
train_score_c2 = svc.score(train_features, train_labels)
test_score_c2 = svc.score(test_features, test_labels)
print(f"Classical SVC on the training dataset: {train_score_c2:.2f}")
print(f"Classical SVC on the test dataset: {test_score_c2:.2f}")
Classical SVC on the training dataset: 0.97
Classical SVC on the test dataset: 0.90
Los resultados siguen siendo buenos pero ligeramente peores en comparación con la versión inicial. Veamos cómo los trata un modelo cuántico. Como ahora tenemos dos qubits, debemos recrear el mapa de características y el ansatz.
[19]:
num_features = features.shape[1]
feature_map = ZZFeatureMap(feature_dimension=num_features, reps=1)
ansatz = RealAmplitudes(num_qubits=num_features, reps=3)
También reducimos la cantidad máxima de iteraciones para las que ejecutamos el proceso de optimización, ya que esperamos que converja más rápido porque ahora tenemos menos qubits.
[20]:
optimizer = COBYLA(maxiter=40)
Ahora construimos un clasificador cuántico a partir de los nuevos parámetros y lo entrenamos.
[21]:
vqc = VQC(
sampler=sampler,
feature_map=feature_map,
ansatz=ansatz,
optimizer=optimizer,
callback=callback_graph,
)
# clear objective value history
objective_func_vals = []
# make the objective function plot look nicer.
plt.rcParams["figure.figsize"] = (12, 6)
start = time.time()
vqc.fit(train_features, train_labels)
elapsed = time.time() - start
print(f"Training time: {round(elapsed)} seconds")
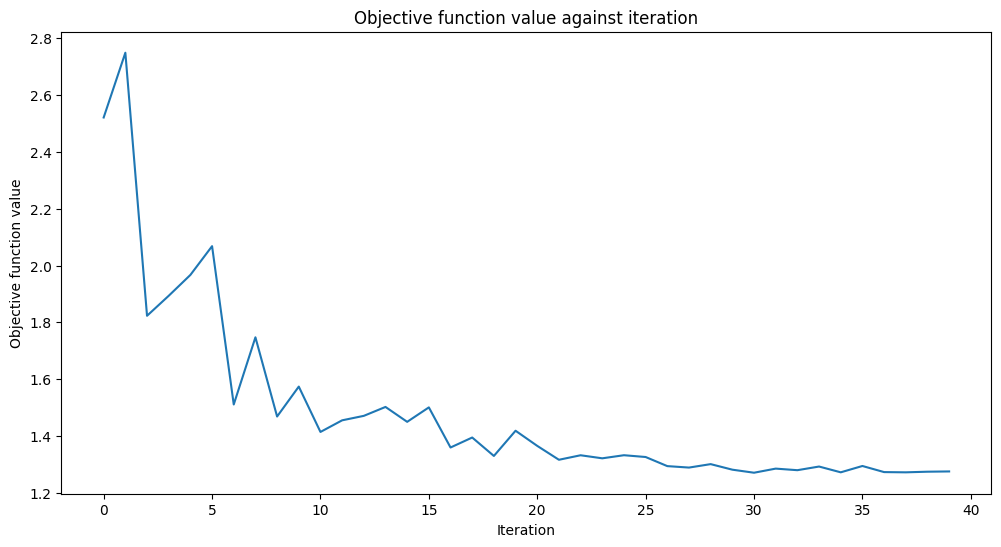
Training time: 58 seconds
[22]:
train_score_q2_ra = vqc.score(train_features, train_labels)
test_score_q2_ra = vqc.score(test_features, test_labels)
print(f"Quantum VQC on the training dataset using RealAmplitudes: {train_score_q2_ra:.2f}")
print(f"Quantum VQC on the test dataset using RealAmplitudes: {test_score_q2_ra:.2f}")
Quantum VQC on the training dataset using RealAmplitudes: 0.58
Quantum VQC on the test dataset using RealAmplitudes: 0.63
Bueno, las puntuaciones son más altas que en un lanzamiento de moneda balanceada, pero podrían ser mejores. La función objetivo es casi plana hacia el final, lo que significa que aumentar el número de iteraciones no ayudará y el rendimiento del modelo seguirá siendo el mismo. Veamos qué podemos hacer con otro ansatz.
[23]:
from qiskit.circuit.library import EfficientSU2
ansatz = EfficientSU2(num_qubits=num_features, reps=3)
optimizer = COBYLA(maxiter=40)
vqc = VQC(
sampler=sampler,
feature_map=feature_map,
ansatz=ansatz,
optimizer=optimizer,
callback=callback_graph,
)
# clear objective value history
objective_func_vals = []
start = time.time()
vqc.fit(train_features, train_labels)
elapsed = time.time() - start
print(f"Training time: {round(elapsed)} seconds")
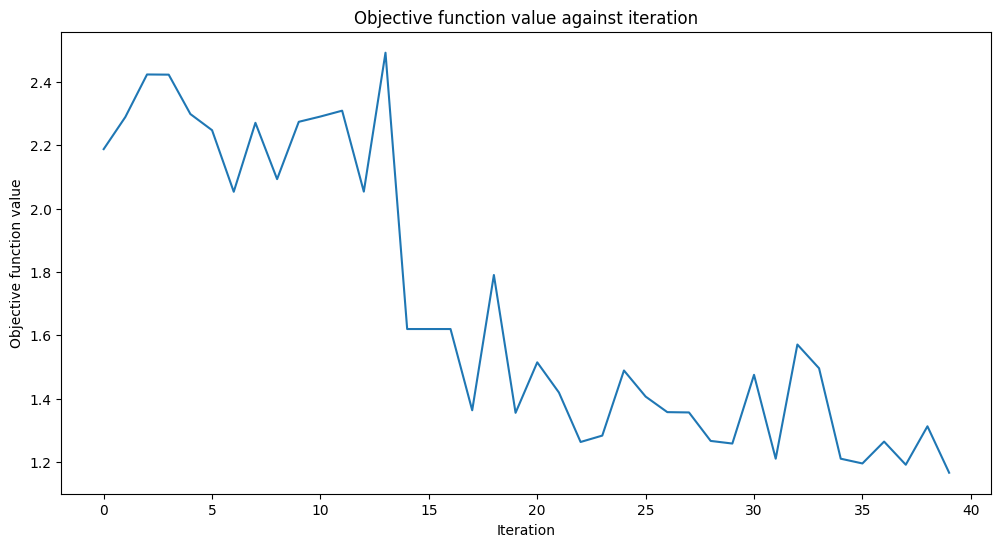
Training time: 74 seconds
[23]:
train_score_q2_eff = vqc.score(train_features, train_labels)
test_score_q2_eff = vqc.score(test_features, test_labels)
print(f"Quantum VQC on the training dataset using EfficientSU2: {train_score_q2_eff:.2f}")
print(f"Quantum VQC on the test dataset using EfficientSU2: {test_score_q2_eff:.2f}")
Quantum VQC on the training dataset using EfficientSU2: 0.78
Quantum VQC on the test dataset using EfficientSU2: 0.80
Las puntuaciones son mejores que en la configuración anterior. Quizás si hubiéramos usado más iteraciones, podríamos hacerlo aún mejor.
5. Conclusión#
En este tutorial, hemos construido dos modelos de machine learning clásicos y tres cuánticos. Imprimamos una tabla general con nuestros resultados.
[24]:
print(f"Model | Test Score | Train Score")
print(f"SVC, 4 features | {train_score_c4:10.2f} | {test_score_c4:10.2f}")
print(f"VQC, 4 features, RealAmplitudes | {train_score_q4:10.2f} | {test_score_q4:10.2f}")
print(f"----------------------------------------------------------")
print(f"SVC, 2 features | {train_score_c2:10.2f} | {test_score_c2:10.2f}")
print(f"VQC, 2 features, RealAmplitudes | {train_score_q2_ra:10.2f} | {test_score_q2_ra:10.2f}")
print(f"VQC, 2 features, EfficientSU2 | {train_score_q2_eff:10.2f} | {test_score_q2_eff:10.2f}")
Model | Test Score | Train Score
SVC, 4 features | 0.99 | 0.97
VQC, 4 features, RealAmplitudes | 0.85 | 0.87
----------------------------------------------------------
SVC, 2 features | 0.97 | 0.90
VQC, 2 features, RealAmplitudes | 0.58 | 0.63
VQC, 2 features, EfficientSU2 | 0.78 | 0.80
Como era de esperar, los modelos clásicos funcionan mejor que sus homólogos cuánticos, pero el ML clásico ha recorrido un largo camino y el ML cuántico aún tiene que alcanzar ese nivel de madurez. Como podemos ver, logramos los mejores resultados utilizando una máquina de vectores de soporte clásica. Pero el modelo cuántico entrenado con cuatro características también fue bastante bueno. Cuando redujimos la cantidad de características, el rendimiento de todos los modelos disminuyó como se esperaba. Por lo tanto, si los recursos permiten entrenar un modelo en un conjunto de datos con todas las características sin ninguna reducción, debes entrenar dicho modelo. De lo contrario, es posible que te comprometas entre el tamaño del conjunto de datos, el tiempo de entrenamiento y la puntuación.
Otra observación es que incluso un simple cambio de ansatz puede conducir a mejores resultados. El modelo de dos características con el ansatz EfficientSU2 funciona mejor que el de RealAmplitudes. Eso significa que la elección de los hiperparámetros desempeña el mismo papel fundamental en el ML cuántico que en el ML clásico, y la búsqueda de hiperparámetros óptimos puede llevar mucho tiempo. Puedes aplicar las mismas técnicas que usamos en el ML clásico, como la aleatoriedad/cuadrícula o enfoques más sofisticados.
Esperamos que este breve tutorial te ayude a dar el salto del ML clásico al ML cuántico.
[25]:
import qiskit.tools.jupyter
%qiskit_version_table
%qiskit_copyright
Version Information
| Qiskit Software | Version |
|---|---|
qiskit-terra | 0.22.0 |
qiskit-aer | 0.11.0 |
qiskit-ignis | 0.7.0 |
qiskit | 0.33.0 |
qiskit-machine-learning | 0.5.0 |
| System information | |
| Python version | 3.7.9 |
| Python compiler | MSC v.1916 64 bit (AMD64) |
| Python build | default, Aug 31 2020 17:10:11 |
| OS | Windows |
| CPUs | 4 |
| Memory (Gb) | 31.837730407714844 |
| Fri Oct 14 14:33:06 2022 GMT Daylight Time | |
This code is a part of Qiskit
© Copyright IBM 2017, 2022.
This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.