Nota
Esta página fue generada a partir de docs/tutorials/11_quantum_convolutional_neural_networks.ipynb.
La Red Neuronal Convolucional Cuántica#
1. Introducción#
A lo largo de este tutorial, analizamos una red neuronal convolucional cuántica (Quantum Convolutional Neural Network, QCNN), propuesta por primera vez por Cong et. al. [1]. Implementamos una QCNN de este tipo en Qiskit mediante el modelado de las capas convolucionales y las capas de agrupación mediante un circuito cuántico. Después de construir una red de este tipo, la entrenamos para diferenciar las líneas horizontales y verticales de una imagen pixelada. El siguiente tutorial se divide en consecuencia;
Diferencias entre una QCNN y una CCNN
Componentes de una QCNN
Generación de Datos
Construir una QCNN
Entrenar nuestra QCNN
Probar nuestra QCNN
Referencias
Primero comenzamos importando las bibliotecas y los paquetes que necesitaremos para este tutorial.
[1]:
import json
import matplotlib.pyplot as plt
import numpy as np
from IPython.display import clear_output
from qiskit import QuantumCircuit
from qiskit.circuit import ParameterVector
from qiskit.circuit.library import ZFeatureMap
from qiskit.quantum_info import SparsePauliOp
from qiskit_algorithms.optimizers import COBYLA
from qiskit_algorithms.utils import algorithm_globals
from qiskit_machine_learning.algorithms.classifiers import NeuralNetworkClassifier
from qiskit_machine_learning.neural_networks import EstimatorQNN
from sklearn.model_selection import train_test_split
algorithm_globals.random_seed = 12345
1. Diferencias entre una QCNN y una CCNN#
1.1 Redes Neuronales Convolucionales Clásicas#
Las Redes Neuronales Convolucionales Clásicas (Classical Convolutional Neural Networks, CCNN) son una subclase de redes neuronales artificiales que tienen la capacidad de determinar características y patrones particulares de una entrada determinada. Debido a esto, se utilizan comúnmente en el reconocimiento de imágenes y el procesamiento de audio.
La capacidad de determinar características es el resultado de los dos tipos de capas que se utilizan en una CCNN, la capa convolucional y la capa de reducción (pooling).
Se puede ver un ejemplo de CCNN en la Figura 1, donde se entrena a una CCNN para determinar si una imagen de entrada contiene un gato o un perro. Para hacerlo, la imagen de entrada pasa a través de una serie de capas alternas convolucionales (C) y de reducción (P), todas las cuales detectan patrones y asocian cada patrón a un gato o un perro. La capa totalmente conectada (FC) nos proporciona una salida que nos permite determinar si la imagen de entrada era un gato o un perro.
La capa convolucional utiliza un kernel, que puede determinar características y patrones de una entrada en particular. Un ejemplo de esto es la detección de características en una imagen, donde diferentes capas detectan patrones particulares en la imagen de entrada. Esto se demuestra en la Figura 1, donde la capa \(l^{th}\) reconoce características y patrones a lo largo del plano \(ij\). Luego, puede asociar dichas características con un resultado dado en el proceso de entrenamiento y puede usar este proceso para entrenar el conjunto de datos.
Por otro lado, una capa de reducción (pooling) reduce la dimensionalidad de los datos de entrada, reduciendo el costo computacional y la cantidad de parámetros de aprendizaje en la CCNN. A continuación se puede ver un esquema de una CCNN.
Para obtener más información sobre CCNN, consulta [2].
Figura 1. Una demostración esquemática del uso de una CCNN para clasificar entre imágenes de un gato y un perro. Aquí, vemos que se aplican varias capas convolucionales y de reducción, todas están disminuyendo en dimensionalidad debido al uso de las capas de reducción. La salida de la CCNN determina si la imagen de entrada era un gato o un perro. Imagen obtenida de [1].
1.2 Redes Neuronales Convolucionales Cuánticas#
Las Redes Neuronales Convolucionales Cuánticas (Quantum Convolutional Neural Networks, QCNN) se comportan de manera similar a las CCNN. Primero, codificamos nuestra imagen pixelada en un circuito cuántico utilizando un mapa de características determinado, como ZFeatureMap o ZZFeatureMap de Qiskit u otros disponibles en la biblioteca de circuitos.
Después de codificar nuestra imagen, aplicamos capas convolucionales y de reducción (pooling) alternas, como se define en la siguiente sección. Al aplicar estas capas alternas, reducimos la dimensionalidad de nuestro circuito hasta que nos quedamos con un qubit. Luego podemos clasificar nuestra imagen de entrada midiendo la salida de este qubit restante.
La Capa Convolucional Cuántica consistirá en una serie de operadores unitarios de dos qubits, que reconocen y determinan las relaciones entre los qubits en nuestro circuito. Estas compuertas unitarias se definen a continuación en la siguiente sección.
Para la Capa de Reducción Cuántica, no podemos hacer lo mismo que se hace clásicamente para reducir la dimensión, es decir, la cantidad de qubits en nuestro circuito. En cambio, reducimos la cantidad de qubits realizando operaciones en cada uno hasta un punto específico y luego ignoramos ciertos qubits en una capa específica. Son estas capas donde dejamos de realizar operaciones en ciertos qubits que llamamos nuestra “capa de reducción”. Los detalles de la capa de reducción se analizan más a fondo en la siguiente sección.
En QCNN, cada capa contiene circuitos parametrizados, lo que significa que alteramos nuestro resultado de salida ajustando los parámetros de cada capa. Al entrenar nuestra QCNN, son estos parámetros los que se ajustan para reducir la función de pérdida de nuestra QCNN.
A continuación se puede ver un ejemplo simple de QCNN de cuatro qubits.
Figura 2: Ejemplo de QCNN que contiene cuatro qubits. La primera Capa Convolucional actúa sobre todos los qubits. A esto le sigue la primera capa de reducción, que disminuye la dimensionalidad de la QCNN de cuatro qubits a dos qubits al ignorar los dos primeros. Luego, la segunda Capa Convolucional detecta características entre los dos qubits que aún están en uso en la QCNN, seguida de otra capa de reducción, que disminuye la dimensionalidad de dos qubits a uno, que será nuestro qubit de salida.
2. Componentes de una QCNN#
Como se discutió en la Sección 1 de este tutorial, una CCNN contendrá capas convolucionales y de reducción (agrupación). Aquí, definimos estas capas para la QCNN en términos de compuertas aplicadas a un circuito cuántico y demostramos un ejemplo para cada capa para 4 qubits.
Cada una de estas capas contendrá parámetros que se ajustan a lo largo del proceso de entrenamiento para minimizar la función de pérdida y entrenar a la QCNN para clasificar entre líneas horizontales y verticales.
En teoría, se podría aplicar cualquier circuito parametrizado para las capas convolucional y de reducción de nuestra red. Por ejemplo, en [2], las Matrices de Gellmann (que son la generalización tridimensional de las Matrices de Pauli) se utilizan como generadores para cada compuerta unitaria que actúa sobre un par de qubits.
Aquí, tomamos un enfoque diferente y formamos nuestro circuito parametrizado basado en la unitaria de dos qubits como se propone en [3]. Esto establece que cada matriz unitaria en \(U(4)\) se puede descomponer de tal manera que
donde \(A_j \in \text{SU}(2)\), \(\otimes\) es el producto tensorial, y \(N(\alpha, \beta, \gamma) = exp(i[\alpha \sigma_x\sigma_x + \beta \sigma_y\sigma_y + \gamma \sigma_z\sigma_z ])\), donde \(\alpha, \beta, \gamma\) son los parámetros que podemos ajustar.
A partir de esto, es evidente que cada unitaria depende de 15 parámetros e implica que para que la QCNN pueda abarcar todo el espacio de Hilbert, cada unitaria en nuestra QCNN debe contener 15 parámetros cada una.
Ajustar esta gran cantidad de parámetros sería difícil y daría lugar a largos tiempos de entrenamiento. Para superar este problema, restringimos nuestro ansatz a un subespacio particular del espacio de Hilbert y definimos la compuerta unitaria de dos qubits como \(N(\alpha, \beta, \gamma)\). Estas unitarias dos qubits, como se muestra en [3], se pueden ver a continuación y se aplican a todos los qubits vecinos de cada una de las capas de la QCNN.
Ten en cuenta que al usar solo \(N(\alpha, \beta, \gamma)\) como nuestra unitaria de dos qubits para las capas parametrizadas, estamos restringiendo nuestra QCNN a un subespacio particular, uno en el que la solución óptima puede no estar contenida y reduciendo la precisión de la QCNN. A los efectos de este tutorial, utilizaremos este circuito parametrizado para disminuir el tiempo de entrenamiento de nuestra QCNN.
Figura 3: Circuito unitario parametrizado de dos qubits para \(N(\alpha, \beta, \gamma) = exp(i[\alpha \sigma_x\sigma_x + \beta \sigma_y\sigma_y + \gamma \sigma_z\sigma_z ])\) como se ve en [3], donde \(\alpha = \frac{\pi}{2} - 2\theta\), \(\beta = 2\phi - \frac{\pi}{2}\) y \(\gamma = \frac{\pi}{2} - 2\lambda\) como se ve en el circuito. Esta unitaria de dos qubits se aplicará a todos los qubits vecinos en nuestro mapa de funciones.
2.1 Capa Convolucional#
El siguiente paso en este tutorial es definir las Capas Convolucionales de nuestra QCNN. Luego, estas capas se aplican a los qubits después de que los datos se hayan codificado mediante el uso del mapa de características.
Para hacerlo, primero debemos determinar una compuerta unitaria parametrizada, que se utilizará para crear nuestras capas convolucionales y de reducción.
[2]:
# We now define a two qubit unitary as defined in [3]
def conv_circuit(params):
target = QuantumCircuit(2)
target.rz(-np.pi / 2, 1)
target.cx(1, 0)
target.rz(params[0], 0)
target.ry(params[1], 1)
target.cx(0, 1)
target.ry(params[2], 1)
target.cx(1, 0)
target.rz(np.pi / 2, 0)
return target
# Let's draw this circuit and see what it looks like
params = ParameterVector("θ", length=3)
circuit = conv_circuit(params)
circuit.draw("mpl", style="clifford")
[2]:
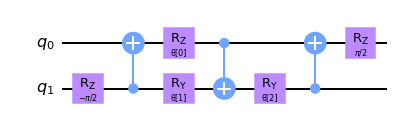
Ahora que hemos definido estas unitarias, es hora de crear una función para la capa convolucional en nuestra QCNN. Para hacerlo, aplicamos la unitaria de dos qubits a los qubits vecinos como se ve en la función conv_layer a continuación.
Ten en cuenta que primero aplicamos la unitaria de dos qubits a todas las parejas de qubits que son pares seguidos de la aplicación a las parejas impares de qubits de manera circular, es decir, los qubits vecinos y los qubits que se acoplan, el primer y último qubit también se acoplan a través de una compuerta unitaria.
Ten en cuenta que agregamos barreras en nuestros circuitos cuánticos por conveniencia al graficar, sin embargo, no son necesarias para la QCNN real y se pueden extraer de los siguientes circuitos.
[3]:
def conv_layer(num_qubits, param_prefix):
qc = QuantumCircuit(num_qubits, name="Convolutional Layer")
qubits = list(range(num_qubits))
param_index = 0
params = ParameterVector(param_prefix, length=num_qubits * 3)
for q1, q2 in zip(qubits[0::2], qubits[1::2]):
qc = qc.compose(conv_circuit(params[param_index : (param_index + 3)]), [q1, q2])
qc.barrier()
param_index += 3
for q1, q2 in zip(qubits[1::2], qubits[2::2] + [0]):
qc = qc.compose(conv_circuit(params[param_index : (param_index + 3)]), [q1, q2])
qc.barrier()
param_index += 3
qc_inst = qc.to_instruction()
qc = QuantumCircuit(num_qubits)
qc.append(qc_inst, qubits)
return qc
circuit = conv_layer(4, "θ")
circuit.decompose().draw("mpl", style="clifford")
[3]:
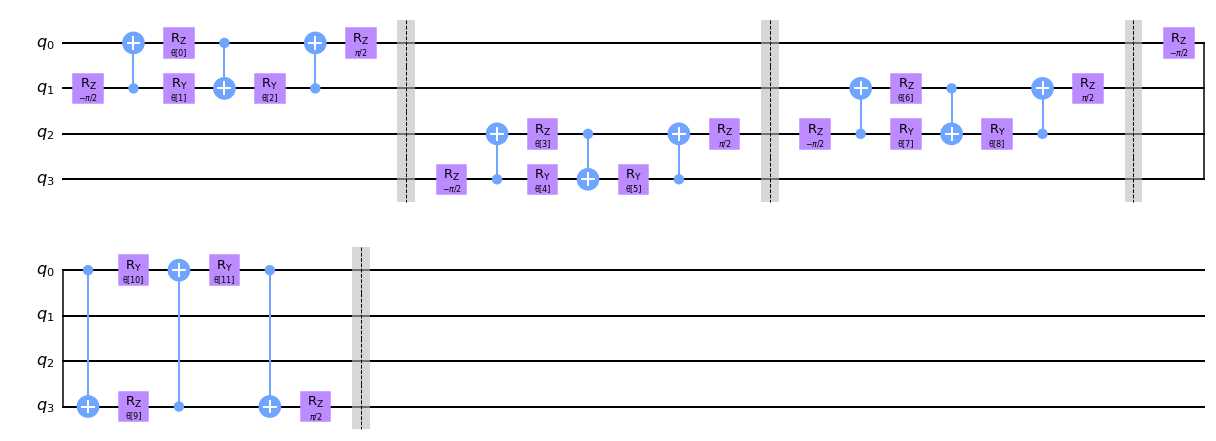
2.2 Capa de Reducción#
El propósito de una capa de agrupación (pooling) es reducir las dimensiones de nuestro circuito cuántico, es decir, reducir la cantidad de qubits en nuestro circuito, mientras que conserva la mayor cantidad de información posible de los datos aprendidos previamente. Reducir la cantidad de qubits también reduce el costo computacional del circuito general, ya que disminuye la cantidad de parámetros que la QCNN necesita aprender.
Sin embargo, uno no puede simplemente disminuir la cantidad de qubits en nuestro circuito cuántico. Debido a esto, debemos definir la capa de reducción de una manera diferente en comparación con el enfoque clásico.
Para reducir “artificialmente” la cantidad de qubits en nuestro circuito, primero comenzamos creando pares de \(N\) qubits en nuestro sistema.
Después de emparejar inicialmente todos los qubits, aplicamos nuestra unitaria generalizada de 2 qubits a cada par, como se describió anteriormente. Después de aplicar esta unitaria de dos qubits, ignoramos un qubit de cada par de qubits para el resto de la red neuronal.
Por lo tanto, esta capa tiene el efecto general de “combinar” la información de los dos qubits en un qubit aplicando primero la unitaria de circuito, codificando la información de un qubit a otro, antes de descartar uno de los qubits para el resto del circuito y no realizar ninguna operación ni medición en él.
Observamos que también se podría aplicar un circuito dinámico para reducir la dimensionalidad en las capas de reducción. Esto implicaría realizar mediciones en ciertos qubits en el circuito y tener un ciclo de retroalimentación clásico intermedio en nuestras capas de reducción. Al aplicar estas mediciones, también se estaría reduciendo la dimensionalidad del circuito.
En este tutorial, aplicamos el enfoque anterior e ignoramos los qubits en cada capa de reducción. Con este enfoque, creamos una Capa de Reducción de la QCNN que transforma las dimensiones de nuestro circuito cuántico de \(N\) qubits en \(N/2\).
Para hacerlo, primero definimos una unitaria de dos qubits, que transforma el sistema de dos qubits en uno.
[4]:
def pool_circuit(params):
target = QuantumCircuit(2)
target.rz(-np.pi / 2, 1)
target.cx(1, 0)
target.rz(params[0], 0)
target.ry(params[1], 1)
target.cx(0, 1)
target.ry(params[2], 1)
return target
params = ParameterVector("θ", length=3)
circuit = pool_circuit(params)
circuit.draw("mpl", style="clifford")
[4]:
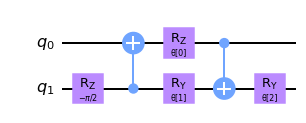
Después de aplicar este circuito unitario de dos qubits, ignoramos el primer qubit (q0) en capas futuras y solo usamos el segundo qubit (q1) en nuestra QCNN
Aplicamos esta capa de reducción de dos qubits a diferentes pares de qubits para crear nuestra capa de reducción para N qubits. Como ejemplo, lo graficamos para cuatro qubits.
[5]:
def pool_layer(sources, sinks, param_prefix):
num_qubits = len(sources) + len(sinks)
qc = QuantumCircuit(num_qubits, name="Pooling Layer")
param_index = 0
params = ParameterVector(param_prefix, length=num_qubits // 2 * 3)
for source, sink in zip(sources, sinks):
qc = qc.compose(pool_circuit(params[param_index : (param_index + 3)]), [source, sink])
qc.barrier()
param_index += 3
qc_inst = qc.to_instruction()
qc = QuantumCircuit(num_qubits)
qc.append(qc_inst, range(num_qubits))
return qc
sources = [0, 1]
sinks = [2, 3]
circuit = pool_layer(sources, sinks, "θ")
circuit.decompose().draw("mpl", style="clifford")
[5]:
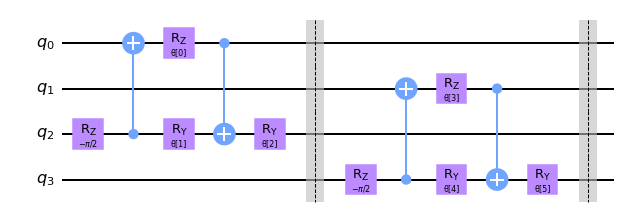
En este ejemplo particular, reducimos la dimensionalidad de nuestro circuito de cuatro qubits a dos qubits, es decir, los dos últimos qubits en este ejemplo particular. Estos qubits luego se usan en la siguiente capa, mientras que los dos primeros se ignoran por el resto de la QCNN.
3. Generación de Datos#
Un uso común de una CCNN es un clasificador de imágenes, donde una CCNN detecta características y patrones particulares (como líneas rectas o curvas) de las imágenes pixeladas mediante el uso de mapas de características en la capa convolucional. Al aprender la relación entre estas características, puede clasificar y etiquetar los dígitos escritos a mano con facilidad.
Debido a la capacidad de una CNN clásica para reconocer características y patrones fácilmente, entrenaremos a nuestra QCNN para que también determine patrones y características de un conjunto dado de imágenes pixeladas y clasifique entre dos patrones diferentes.
Para simplificar el conjunto de datos, solo consideramos imágenes pixeladas de 2 x 4. Los patrones que entrenaremos en la QCNN para distinguir serán una línea horizontal o vertical, que se puede colocar en cualquier lugar de la imagen, junto con un fondo ruidoso.
Primero comenzamos generando este conjunto de datos. Para crear una línea “horizontal” o “vertical”, asignamos el valor de pixeles para que sea \(\frac{\pi}{2}\), que representará la línea en nuestra imagen pixelada. Creamos un fondo ruidoso asignando alternadamente a un pixel si y a otro no, un valor aleatorio entre \(0\) y \(\frac{\pi}{4}\) lo que creará un fondo ruidoso.
Ten en cuenta que cuando creamos nuestro conjunto de datos, debemos dividirlo en el conjunto de imágenes de entrenamiento y en el conjunto de imágenes de prueba, los conjuntos de datos con los que entrenamos y probamos nuestra red neuronal, respectivamente.
También necesitamos etiquetar nuestros conjuntos de datos de manera que la QCNN pueda aprender a diferenciar entre los dos patrones. En este ejemplo, etiquetamos las imágenes con una línea horizontal con -1 y las imágenes con una línea vertical +1.
[6]:
def generate_dataset(num_images):
images = []
labels = []
hor_array = np.zeros((6, 8))
ver_array = np.zeros((4, 8))
j = 0
for i in range(0, 7):
if i != 3:
hor_array[j][i] = np.pi / 2
hor_array[j][i + 1] = np.pi / 2
j += 1
j = 0
for i in range(0, 4):
ver_array[j][i] = np.pi / 2
ver_array[j][i + 4] = np.pi / 2
j += 1
for n in range(num_images):
rng = algorithm_globals.random.integers(0, 2)
if rng == 0:
labels.append(-1)
random_image = algorithm_globals.random.integers(0, 6)
images.append(np.array(hor_array[random_image]))
elif rng == 1:
labels.append(1)
random_image = algorithm_globals.random.integers(0, 4)
images.append(np.array(ver_array[random_image]))
# Create noise
for i in range(8):
if images[-1][i] == 0:
images[-1][i] = algorithm_globals.random.uniform(0, np.pi / 4)
return images, labels
Let’s now create our dataset below and split it into our test and training datasets. We pass a random_state so the split will be the same each time this notebook is run so the final results do not vary.
[7]:
images, labels = generate_dataset(50)
train_images, test_images, train_labels, test_labels = train_test_split(
images, labels, test_size=0.3, random_state=246
)
Veamos algunos ejemplos en nuestro conjunto de datos
[8]:
fig, ax = plt.subplots(2, 2, figsize=(10, 6), subplot_kw={"xticks": [], "yticks": []})
for i in range(4):
ax[i // 2, i % 2].imshow(
train_images[i].reshape(2, 4), # Change back to 2 by 4
aspect="equal",
)
plt.subplots_adjust(wspace=0.1, hspace=0.025)

Como podemos ver, cada imagen contiene una línea vertical u horizontal, que la QCNN aprenderá a diferenciar. Ahora que hemos construido nuestro conjunto de datos, es hora de discutir los componentes de la QCNN y construir nuestro modelo.
4. Modelar nuestra QCNN#
Ahora que hemos definido ambas capas convolucionales, es el momento de construir nuestra QCNN, que consistirá en capas alternas de reducción y convolucionales.
Como las imágenes en nuestro conjunto de datos contienen 8 píxeles, usaremos 8 qubits en nuestra QCNN.
Codificamos nuestro conjunto de datos en nuestra QCNN aplicando un mapa de características. Se puede crear un mapa de características utilizando uno de los mapas de funciones integrados de Qiskit, como ZFeatureMap o ZZFeatureMap.
Después de analizar varios mapas de características diferentes para este conjunto de datos, se encontró que la QCNN obtiene la mayor precisión cuando se usa el mapa de características Z. Por lo tanto, durante el resto del tutorial utilizaremos el mapa de características Z, como se puede ver a continuación.
[9]:
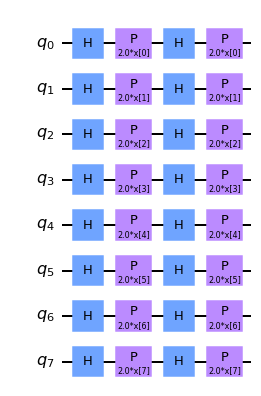
feature_map = ZFeatureMap(8)
feature_map.decompose().draw("mpl", style="clifford")
[9]:
Creamos una función para nuestra QCNN, que contendrá tres conjuntos de capas convolucionales y de reducción alternas, que se pueden ver en el siguiente esquema. Mediante el uso de las capas de agrupación (pooling), reducimos la dimensionalidad de nuestra QCNN de ocho qubits a uno.
Para clasificar nuestro conjunto de datos de imágenes de líneas horizontales y verticales, medimos el valor esperado del operador de Pauli Z del qubit final. Según el valor obtenido +1 o -1, podemos concluir que la imagen de entrada contenía una línea horizontal o vertical.
5. Entrenar nuestra QCNN#
El siguiente paso es construir nuestro modelo usando nuestros datos de entrenamiento.
Para clasificar nuestro sistema, realizamos una medición desde el circuito de salida. El valor que obtengamos clasificará si nuestros datos de entrada contienen una línea vertical o una línea horizontal.
La medición que hemos elegido en este tutorial es \(<Z>\), es decir, el valor esperado de la Pauli Z para el qubit final. Midiendo este valor esperado, obtenemos +1 o -1, que corresponden a una línea vertical u horizontal respectivamente.
[10]:
feature_map = ZFeatureMap(8)
ansatz = QuantumCircuit(8, name="Ansatz")
# First Convolutional Layer
ansatz.compose(conv_layer(8, "c1"), list(range(8)), inplace=True)
# First Pooling Layer
ansatz.compose(pool_layer([0, 1, 2, 3], [4, 5, 6, 7], "p1"), list(range(8)), inplace=True)
# Second Convolutional Layer
ansatz.compose(conv_layer(4, "c2"), list(range(4, 8)), inplace=True)
# Second Pooling Layer
ansatz.compose(pool_layer([0, 1], [2, 3], "p2"), list(range(4, 8)), inplace=True)
# Third Convolutional Layer
ansatz.compose(conv_layer(2, "c3"), list(range(6, 8)), inplace=True)
# Third Pooling Layer
ansatz.compose(pool_layer([0], [1], "p3"), list(range(6, 8)), inplace=True)
# Combining the feature map and ansatz
circuit = QuantumCircuit(8)
circuit.compose(feature_map, range(8), inplace=True)
circuit.compose(ansatz, range(8), inplace=True)
observable = SparsePauliOp.from_list([("Z" + "I" * 7, 1)])
# we decompose the circuit for the QNN to avoid additional data copying
qnn = EstimatorQNN(
circuit=circuit.decompose(),
observables=observable,
input_params=feature_map.parameters,
weight_params=ansatz.parameters,
)
[11]:
circuit.draw("mpl", style="clifford")
[11]:
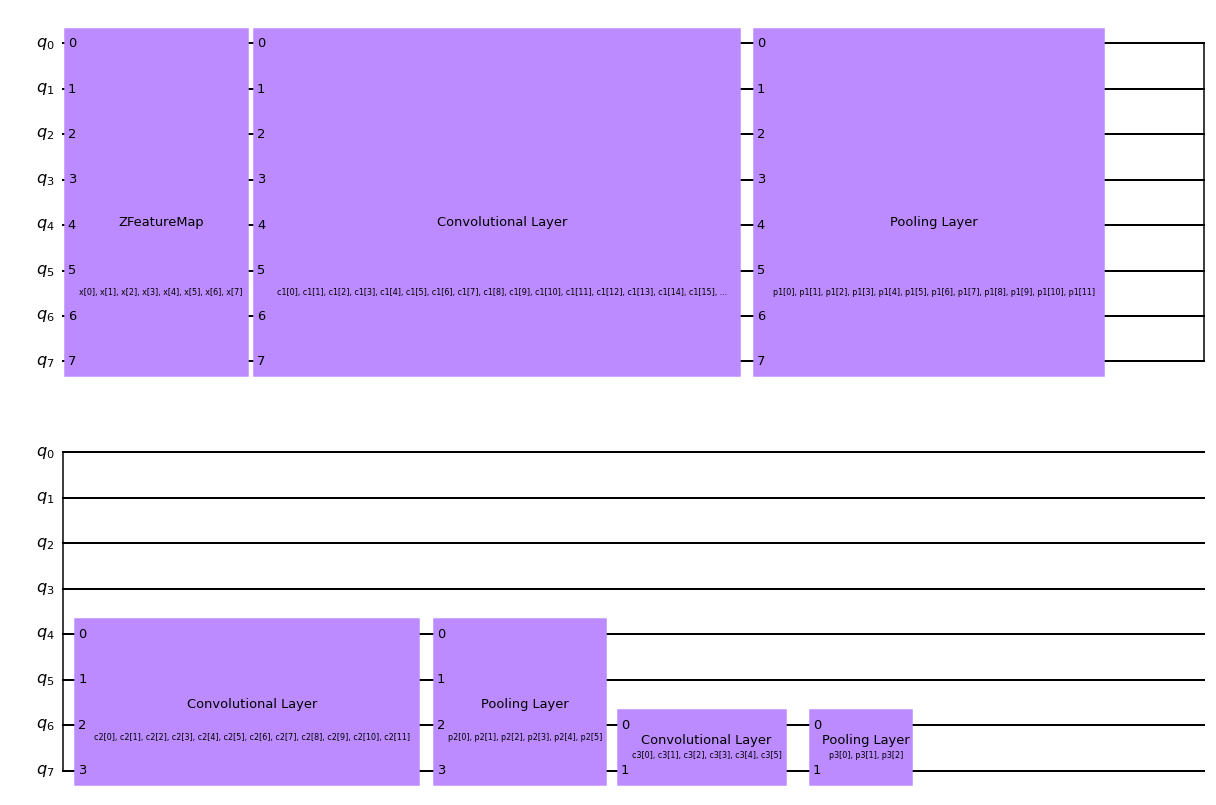
También definiremos una función de devolución de llamada para usar al entrenar nuestro modelo. Esto nos permite ver y graficar la función de pérdida por cada iteración en nuestro proceso de entrenamiento.
[12]:
def callback_graph(weights, obj_func_eval):
clear_output(wait=True)
objective_func_vals.append(obj_func_eval)
plt.title("Objective function value against iteration")
plt.xlabel("Iteration")
plt.ylabel("Objective function value")
plt.plot(range(len(objective_func_vals)), objective_func_vals)
plt.show()
En este ejemplo, usaremos el optimizador COBYLA para entrenar nuestro clasificador, que es un método de optimización numérica comúnmente utilizado para clasificar algoritmos de machine learning.
Luego colocamos la función de devolución de llamada, el optimizador y el operador de nuestra QCNN creada anteriormente en el Clasificador de Redes Neuronales integrado de Qiskit Machine Learning, que luego podemos usar para entrenar nuestro modelo.
Dado que el entrenamiento del modelo puede llevar mucho tiempo, ya hemos entrenado previamente el modelo para algunas iteraciones y hemos guardado los pesos previamente entrenados. Continuaremos entrenando desde ese punto configurando initial_point a un vector de pesos preentrenados.
[13]:
with open("11_qcnn_initial_point.json", "r") as f:
initial_point = json.load(f)
classifier = NeuralNetworkClassifier(
qnn,
optimizer=COBYLA(maxiter=200), # Set max iterations here
callback=callback_graph,
initial_point=initial_point,
)
Después de crear este clasificador, podemos entrenar nuestra QCNN usando nuestro conjunto de datos de entrenamiento y la etiqueta correspondiente de cada imagen. Debido a que previamente definimos la función de devolución de llamada, graficamos la pérdida general de nuestro sistema por iteración.
¡Puede tomar algún tiempo entrenar la QCNN, así que ten paciencia!
[14]:
x = np.asarray(train_images)
y = np.asarray(train_labels)
objective_func_vals = []
plt.rcParams["figure.figsize"] = (12, 6)
classifier.fit(x, y)
# score classifier
print(f"Accuracy from the train data : {np.round(100 * classifier.score(x, y), 2)}%")
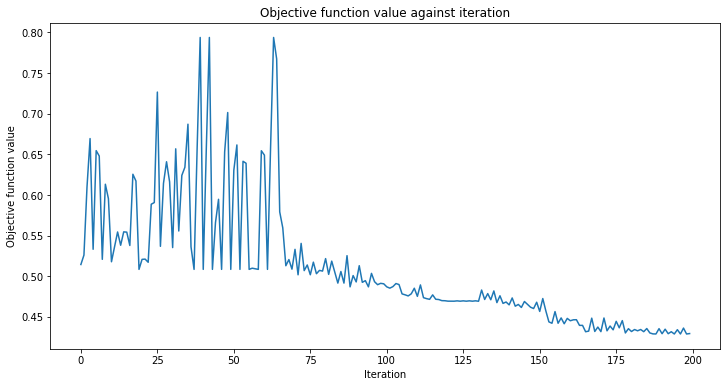
Accuracy from the train data : 97.14%
Como podemos ver desde arriba, la QCNN converge lentamente, por lo que nuestro initial_point ya estaba cerca de una solución óptima. El siguiente paso es determinar si nuestra QCNN puede clasificar los datos vistos en nuestro conjunto de datos de imágenes de prueba.
6. Probar nuestra QCNN#
Después de construir y entrenar nuestro conjunto de datos, ahora probamos si nuestra QCNN puede predecir imágenes que no son de nuestro conjunto de datos de prueba.
[15]:
y_predict = classifier.predict(test_images)
x = np.asarray(test_images)
y = np.asarray(test_labels)
print(f"Accuracy from the test data : {np.round(100 * classifier.score(x, y), 2)}%")
# Let's see some examples in our dataset
fig, ax = plt.subplots(2, 2, figsize=(10, 6), subplot_kw={"xticks": [], "yticks": []})
for i in range(0, 4):
ax[i // 2, i % 2].imshow(test_images[i].reshape(2, 4), aspect="equal")
if y_predict[i] == -1:
ax[i // 2, i % 2].set_title("The QCNN predicts this is a Horizontal Line")
if y_predict[i] == +1:
ax[i // 2, i % 2].set_title("The QCNN predicts this is a Vertical Line")
plt.subplots_adjust(wspace=0.1, hspace=0.5)
Accuracy from the test data : 93.33%

¡De lo anterior, podemos ver que nuestra QCNN puede clasificar líneas horizontales y verticales! ¡Felicidades! Mediante el uso de circuitos cuánticos y capas cuánticas convolucionales y de reducción (pooling), ¡has creado una Red Neuronal Cuántica Convolucional!
7. Referencias#
[1] Cong, I., Choi, S. & Lukin, M.D. Quantum convolutional neural networks. Nat. Phys. 15, 1273–1278 (2019). https://doi.org/10.1038/s41567-019-0648-8
[2] IBM Convolutional Neural Networks https://www.ibm.com/cloud/learn/convolutional-neural-networks
[3] Vatan, Farrokh, and Colin Williams. «Optimal quantum circuits for general two-qubit gates.» Physical Review A 69.3 (2004): 032315.
[16]:
import qiskit.tools.jupyter
%qiskit_version_table
%qiskit_copyright
Version Information
| Software | Version |
|---|---|
qiskit | 1.0.0.dev0+737f21b |
qiskit_algorithms | 0.3.0 |
qiskit_machine_learning | 0.8.0 |
| System information | |
| Python version | 3.9.7 |
| Python compiler | GCC 7.5.0 |
| Python build | default, Sep 16 2021 13:09:58 |
| OS | Linux |
| CPUs | 2 |
| Memory (Gb) | 5.792198181152344 |
| Thu Dec 14 13:53:25 2023 EST | |
This code is a part of Qiskit
© Copyright IBM 2017, 2023.
This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.