Nota
Esta página fue generada a partir de docs/tutorials/07_pegasos_qsvc.ipynb.
Clasificador Cuántico de Vectores de Soporte tipo Pegasos#
Hay otro algoritmo basado en SVM que se beneficia del método del kernel cuántico. Aquí presentamos una implementación de otro algoritmo de clasificación, que es una versión alternativa al QSVC disponible en Qiskit Machine Learning y que se muestra en el tutorial «Machine Learning con Kernel Cuántico». Este algoritmo de clasificación implementa el algoritmo Pegasos del artículo «Pegasos: Primal Estimated sub-GrAdient SOlver for SVM» de Shalev-Shwartz et al., ver: https://home.ttic.edu/~nati/Publications/PegasosMPB.pdf.
Este algoritmo es una alternativa a la optimización dual del paquete scikit-learn, se beneficia del truco del kernel y produce una complejidad de entrenamiento que es independiente del tamaño del conjunto de entrenamiento. Por lo tanto, se espera que PegasosQSVC entrene más rápido que QSVC para conjuntos de entrenamiento suficientemente grandes.
El algoritmo se puede utilizar como reemplazo directo de QSVC con un poco de hiperparametrización.
Generemos algunos datos:
[1]:
from sklearn.datasets import make_blobs
# example dataset
features, labels = make_blobs(n_samples=20, n_features=2, centers=2, random_state=3, shuffle=True)
Procesamos previamente los datos para garantizar la compatibilidad con la codificación de rotación y los dividimos en conjuntos de datos de entrenamiento y prueba.
[2]:
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
features = MinMaxScaler(feature_range=(0, np.pi)).fit_transform(features)
train_features, test_features, train_labels, test_labels = train_test_split(
features, labels, train_size=15, shuffle=False
)
Tenemos dos características en el conjunto de datos, por lo que establecemos una cantidad de qubits para la cantidad de características en el conjunto de datos.
Luego establecemos \(\tau\) al número de pasos realizados durante el procedimiento de entrenamiento. Ten en cuenta que no existe un criterio de detención anticipada en el algoritmo. El algoritmo itera sobre todos los pasos \(\tau\).
Y el último es el hiperparámetro \(C\). Este es un parámetro de regularización positivo. La magnitud de la regularización es inversamente proporcional a \(C\). Entre más pequeño \(C\) induce pesos más pequeños, lo que generalmente ayuda a prevenir el sobreajuste. Sin embargo, debido a la naturaleza de este algoritmo, algunos de los pasos de cálculo se vuelven triviales para \(C\) más grandes. Por lo tanto, entre más grande \(C\) mejora drásticamente el rendimiento del algoritmo. Si los datos se pueden separar linealmente en el espacio de características, \(C\) debe elegirse para que sea grande. Si la separación no es perfecta, \(C\) debe elegirse más pequeño para evitar el sobreajuste.
[3]:
# number of qubits is equal to the number of features
num_qubits = 2
# number of steps performed during the training procedure
tau = 100
# regularization parameter
C = 1000
El algoritmo se ejecutará usando:
La fidelidad predeterminada instanciada en
FidelityQuantumKernelUn kernel cuántico creado a partir de
ZFeatureMap
[4]:
from qiskit import BasicAer
from qiskit.circuit.library import ZFeatureMap
from qiskit_algorithms.utils import algorithm_globals
from qiskit_machine_learning.kernels import FidelityQuantumKernel
algorithm_globals.random_seed = 12345
feature_map = ZFeatureMap(feature_dimension=num_qubits, reps=1)
qkernel = FidelityQuantumKernel(feature_map=feature_map)
La implementación PegasosQSVC es compatible con las interfaces scikit-learn y tiene una forma bastante estándar de entrenar un modelo. En el constructor pasamos parámetros del algoritmo, en este caso hay un hiperparámetro de regularización \(C\) y un número de pasos.
Luego pasamos las características de entrenamiento y las etiquetas al método fit, que entrena un modelo y devuelve un clasificador ajustado.
Luego, calificamos nuestro modelo usando características de prueba y etiquetas.
[5]:
from qiskit_machine_learning.algorithms import PegasosQSVC
pegasos_qsvc = PegasosQSVC(quantum_kernel=qkernel, C=C, num_steps=tau)
# training
pegasos_qsvc.fit(train_features, train_labels)
# testing
pegasos_score = pegasos_qsvc.score(test_features, test_labels)
print(f"PegasosQSVC classification test score: {pegasos_score}")
PegasosQSVC classification test score: 1.0
Para fines de visualización, creamos una cuadrícula de malla de un paso predefinido que abarca nuestros valores mínimo y máximo que aplicamos en MinMaxScaler. También agregamos algo de margen a la cuadrícula para una mejor representación de las muestras de entrenamiento y prueba.
[6]:
grid_step = 0.2
margin = 0.2
grid_x, grid_y = np.meshgrid(
np.arange(-margin, np.pi + margin, grid_step), np.arange(-margin, np.pi + margin, grid_step)
)
Convertimos la cuadrícula a la forma compatible con el modelo, la forma debe ser (n_samples, n_features). Luego, para cada punto de la cuadrícula, predecimos una etiqueta. En nuestro caso, las etiquetas predichas se utilizarán para colorear la cuadrícula.
[7]:
meshgrid_features = np.column_stack((grid_x.ravel(), grid_y.ravel()))
meshgrid_colors = pegasos_qsvc.predict(meshgrid_features)
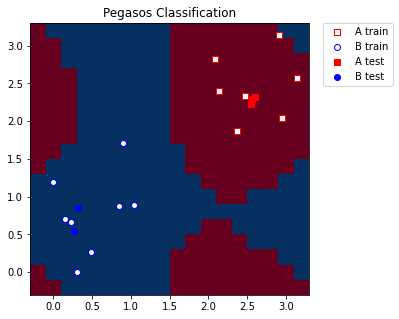
Finalmente, graficamos nuestra cuadrícula de acuerdo con las etiquetas/colores que obtuvimos del modelo. También graficamos las muestras de entrenamiento y prueba.
[8]:
import matplotlib.pyplot as plt
plt.figure(figsize=(5, 5))
meshgrid_colors = meshgrid_colors.reshape(grid_x.shape)
plt.pcolormesh(grid_x, grid_y, meshgrid_colors, cmap="RdBu", shading="auto")
plt.scatter(
train_features[:, 0][train_labels == 0],
train_features[:, 1][train_labels == 0],
marker="s",
facecolors="w",
edgecolors="r",
label="A train",
)
plt.scatter(
train_features[:, 0][train_labels == 1],
train_features[:, 1][train_labels == 1],
marker="o",
facecolors="w",
edgecolors="b",
label="B train",
)
plt.scatter(
test_features[:, 0][test_labels == 0],
test_features[:, 1][test_labels == 0],
marker="s",
facecolors="r",
edgecolors="r",
label="A test",
)
plt.scatter(
test_features[:, 0][test_labels == 1],
test_features[:, 1][test_labels == 1],
marker="o",
facecolors="b",
edgecolors="b",
label="B test",
)
plt.legend(bbox_to_anchor=(1.05, 1), loc="upper left", borderaxespad=0.0)
plt.title("Pegasos Classification")
plt.show()
[9]:
import qiskit.tools.jupyter
%qiskit_version_table
%qiskit_copyright
Version Information
| Qiskit Software | Version |
|---|---|
qiskit-terra | 0.22.0 |
qiskit-aer | 0.11.0 |
qiskit-ignis | 0.7.0 |
qiskit | 0.33.0 |
qiskit-machine-learning | 0.5.0 |
| System information | |
| Python version | 3.7.9 |
| Python compiler | MSC v.1916 64 bit (AMD64) |
| Python build | default, Aug 31 2020 17:10:11 |
| OS | Windows |
| CPUs | 4 |
| Memory (Gb) | 31.837730407714844 |
| Thu Oct 13 10:42:49 2022 GMT Daylight Time | |
This code is a part of Qiskit
© Copyright IBM 2017, 2022.
This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.