Nota
Esta página fue generada a partir de docs/tutorials/12_quantum_autoencoder.ipynb.
El Autocodificador Cuántico#
El objetivo de este tutorial es construir un Autocodificador Cuántico, un circuito que puede comprimir un estado cuántico en una cantidad más pequeña de qubits, mientras retiene la información del estado inicial.
A lo largo de este tutorial, explicamos la arquitectura de un Autocodificador Cuántico y cómo se puede diseñar y entrenar dicho sistema para comprimir y codificar información. Después de esta discusión, damos dos ejemplos para demostrar las capacidades de dicho sistema para comprimir diferentes estados cuánticos, así como la capacidad de comprimir imágenes de ceros y unos.
Contenido#
El siguiente tutorial se desglosa de la siguiente manera:
¿Qué es un Autocodificador?
El Autocodificador Cuántico
Componentes de un Autocodificador Cuántico
Elegir una Función de Pérdida
Construir nuestro Autocodificador
Un Ejemplo Simple: La Pared de Dominio
Un Autocodificador Cuántico para Imágenes Ruidosas de Dígitos
Aplicaciones de un Autocodificador Cuántico
Referencias
1. ¿Qué es un Autocodificador?#
Un autocodificador clásico (classical autoencoder, CAE) es un tipo de arquitectura de red neuronal que se usa comúnmente para comprimir y codificar de manera eficiente la información de la entrada mediante el aprendizaje de representación. Después de la compresión, se pueden descomprimir los datos mediante el uso de un decodificador.
Los autocodificadores típicos se dividen comúnmente en tres capas, como se ve en la Figura 1.
Figura 1: Ejemplo de un Autocodificador Clásico que incluye la capa de entrada, cuello de botella y salida.
La primera capa se llama Capa de Entrada (1) y es la capa en la que ingresamos nuestros datos de longitud \(n\).
Luego, los datos de entrada pasan a través de un codificador y viajan a la siguiente capa, que tiene menos nodos o tiene dimensiones reducidas y se conoce como la capa de Cuello de Botella (2). La capa de entrada se comprime a través de este proceso. Los CAE comunes pueden tener varias capas.
La capa final se llama Capa de Salida (3). Aquí, los datos comprimidos se reconstruyen a su tamaño original, \(n\), a partir de los datos comprimidos mediante el proceso de un decodificador.
Al pasar nuestros datos de entrada a través de un CAE, podemos reducir la dimensionalidad de nuestros datos de entrada, como se ve en la capa de cuello de botella, mientras retenemos la mayor cantidad de información posible de los datos de entrada. Debido a esta característica, los usos comunes del CAE son dispositivos de eliminación de ruido de imagen, detección de anomalías y reconocimiento facial. Para obtener más información sobre los autocodificadores clásicos, consulta [1].
2. El Autocodificador Cuántico#
También podemos definir una contraparte cuántica del CAE, el Autocodificador Cuántico (Quantum Autoencoder). Al igual que el CAE, el Autocodificador Cuántico tiene como objetivo reducir la dimensionalidad de la entrada de la red neuronal, en este caso un estado cuántico. Una representación pictórica de esto se puede ver en la Figura 2.
Figura 2: Representación pictórica de un Autocodificador Cuántico. Aquí se pueden ver las similitudes con el CAE, teniendo el circuito un estado de entrada, un estado de cuello de botella y un estado de salida.
Al igual que su contraparte clásica, nuestro circuito contiene tres capas. Primero ingresamos nuestro estado \(|\psi>\) (que contiene \(n\) qubits), el cual deseamos comprimir. Esta es nuestra capa de entrada (1).
Luego aplicamos nuestro circuito parametrizado en nuestro estado de entrada, que actuará como nuestro codificador y “comprimirá” nuestro estado cuántico, reduciendo la dimensionalidad de nuestro estado a \(n-k\) qubits. Nuestro nuevo estado comprimido tiene la forma \(|\psi_{comp}> \otimes |0>^{\otimes k}\), donde \(|\psi_{comp}>\) contiene \(n-k\) qubits.
Este circuito parametrizado dependerá de un conjunto de parámetros, que serán los nodos de nuestro Autocodificador Cuántico. A lo largo del proceso de entrenamiento, estos parámetros se actualizarán para optimizar la función de pérdida.
Ignoramos los \(k\) qubits restantes para el resto del circuito. Esta es nuestra capa de cuello de botella (2) y nuestro estado de entrada ahora está comprimido.
La capa final consiste en la adición de \(k\) qubits (todos en el estado \(|0\rangle\)) y aplicar otro circuito parametrizado entre el estado comprimido y los nuevos qubits. Este circuito parametrizado actúa como nuestro decodificador y reconstruye el estado de entrada a partir del estado comprimido usando los nuevos qubits. Después del decodificador, retenemos el estado original a medida que el estado viaja a la capa de salida (3).
3. Componentes de un Autocodificador Cuántico#
Antes de construir nuestro Autocodificador Cuántico, debemos tener en cuenta algunas sutilezas.
Primero notamos que no podemos introducir o descartar qubits en medio de un circuito cuántico cuando implementamos un autocodificador usando Qiskit.
Por eso, debemos incluir nuestro estado de referencia, así como nuestros qubits auxiliares (cuya función se describirá en secciones posteriores) al comienzo del circuito.
Por lo tanto, nuestra capa de entrada consistirá en nuestro estado de entrada, el estado de referencia y un qubit auxiliar, así como un registro clásico para realizar mediciones (que se describirá en la siguiente sección). Una representación pictórica de esto se puede ver en la Figura 3.
Figura 3: Representación pictórica del estado de entrada de un Autocodificador Cuántico. Ten en cuenta que también debemos incluir un qubit auxiliar, el estado de referencia y el registro clásico al comienzo del circuito, aunque no se usan hasta más adelante en el circuito.
4. Elegir una Función de Pérdida#
Ahora definimos nuestra función de costo, que usaremos para entrenar nuestro Autocodificador Cuántico, para devolver el estado de entrada. Hay un poco de matemáticas involucradas aquí, ¡así que omite esta sección si no estás interesado!
Tomamos la función de costo como se define en [2], que trata de maximizar la fidelidad entre el estado de entrada y salida de nuestro Autocodificador Cuántico.
Primero definimos los subsistemas \(A\) y \(B\) para contener \(n\) y \(k\) qubits respectivamente, mientras que \(B'\) es el espacio que contendrá nuestro espacio de referencia. Llamamos al subsistema \(A\) nuestro espacio latente, que contendrá el estado de qubit comprimido, y \(B\) nuestro espacio basura, que contiene los qubits que ignoramos durante la compresión.
Por lo tanto, nuestro estado de entrada \(|\psi_{AB}>\) contiene \(n + k\) qubits. Definimos el espacio de referencia \(B'\) que contiene el estado de referencia \(|a>_{B'}\). Este espacio contendrá los \(k\) qubits adicionales que usamos en el decodificador. Todos estos subsistemas se pueden ver en la Figura 3.
Definimos el circuito parametrizado como \(U(\theta)\) que usaremos como nuestro codificador. Sin embargo, la estructura y los parámetros de nuestro circuito parametrizado son actualmente desconocidos para nosotros y pueden variar para diferentes estados de entrada. Para determinar los parámetros para comprimir nuestro estado de entrada, debemos entrenar nuestro dispositivo para comprimir al máximo el estado ajustando los valores de los parámetros \(\theta\). Para el decodificador usaremos \(U^{\dagger}(\theta)\).
Por lo tanto, nuestro objetivo es maximizar la fidelidad entre los estados de entrada y salida, es decir,
donde
Podemos maximizar esta fidelidad ajustando los parámetros \(\theta\) en nuestro circuito parametrizado. Sin embargo, esta fidelidad a veces puede ser complicada de determinar y puede requerir una gran cantidad de compuertas necesarias para calcular la fidelidad entre dos estados, es decir, cuanto mayor es el número de qubits, más compuertas se requieren, lo que da como resultado circuitos más profundos. Por lo tanto, buscamos medios alternativos para comparar los estados de entrada y salida.
Como se muestra en [2], una forma más sencilla de determinar un estado comprimido de manera óptima es realizar una compuerta de intercambio entre el estado basura y el estado de referencia. Estos estados suelen tener una menor cantidad de qubits y, por lo tanto, son más fáciles de comparar debido a la menor cantidad de compuertas requeridas. Como se muestra en [2], maximizar la fidelidad de estos dos estados es equivalente a maximizar la fidelidad del estado de entrada y salida y, en consecuencia, determinar una compresión óptima de nuestro circuito de entrada.
Manteniendo fijo nuestro estado de referencia, nuestra función de costo ahora será una función del estado basura y se denota como;
A lo largo del proceso de entrenamiento, ajustamos los parámetros \(\theta\) en nuestro codificador y realizamos una prueba swap o de intercambio (como se describe a continuación) para determinar la fidelidad entre estos estados basura y de referencia. Al hacerlo, debemos incluir un qubit adicional, nuestro qubit auxiliar, que se usará a lo largo de la prueba swap y se medirá para determinar la fidelidad general de los estados basura y de referencia. Esta es la razón por la que incluimos un qubit auxiliar y un registro clásico en la sección anterior al inicializar nuestro circuito.
La Prueba SWAP#
La Prueba SWAP (prueba de intercambio) es un procedimiento comúnmente utilizado para comparar dos estados mediante la aplicación de compuertas CNOT a cada qubit (para obtener más información, consulta [3]). Al ejecutar el circuito \(M\) veces y aplicar la prueba SWAP, medimos el qubit auxiliar. Usamos el número de estados en el estado \(|1\rangle\) a calcular:
donde \(L\) es el recuento de los estados en el estado \(|1\rangle\). Como se muestra en [3], maximizar esta función corresponde a que los dos estados que estamos comparando sean idénticos. Por lo tanto, nuestro objetivo es maximizar esta función, es decir, minimizar \(\frac{2}{M}L\). Este valor será en consecuencia nuestra función de costo.
5. Construir el Ansatz del Autocodificador Cuántico#
Primero, importamos Qiskit de IBM para construir nuestro Autocodificador Cuántico. Primero comenzamos importando las bibliotecas necesarias y fijando la semilla.
[1]:
import json
import time
import warnings
import matplotlib.pyplot as plt
import numpy as np
from IPython.display import clear_output
from qiskit import ClassicalRegister, QuantumRegister
from qiskit import QuantumCircuit
from qiskit.circuit.library import RealAmplitudes
from qiskit.quantum_info import Statevector
from qiskit_algorithms.optimizers import COBYLA
from qiskit_algorithms.utils import algorithm_globals
from qiskit_machine_learning.circuit.library import RawFeatureVector
from qiskit_machine_learning.neural_networks import SamplerQNN
algorithm_globals.random_seed = 42
Comenzamos definiendo nuestro ansatz parametrizado para el Autocodificador Cuántico. Este será nuestro circuito parametrizado donde podemos ajustar los parámetros para maximizar la fidelidad entre los estados basura y de referencia.
El Circuito Parametrizado#
El circuito parametrizado que usaremos a continuación para nuestro codificador es el Ansatz RealAmplitude disponible en Qiskit. Una de las razones por las que hemos elegido este ansatz es porque es un circuito 2-local, los estados cuánticos preparados solo tendrán amplitudes reales y no dependen de la conectividad completa entre cada qubit, lo cual es difícil de implementar o puede conducir a circuitos profundos.
Definimos nuestro circuito parametrizado para nuestro codificador a continuación, donde configuramos el parámetro de repetición en reps=5, para aumentar la cantidad de parámetros en nuestro circuito y permitir una mayor flexibilidad.
[2]:
def ansatz(num_qubits):
return RealAmplitudes(num_qubits, reps=5)
Dibujemos este ansatz con \(5\) qubits y veamos cómo se ve.
[3]:
num_qubits = 5
circ = ansatz(num_qubits)
circ.decompose().draw("mpl")
[3]:
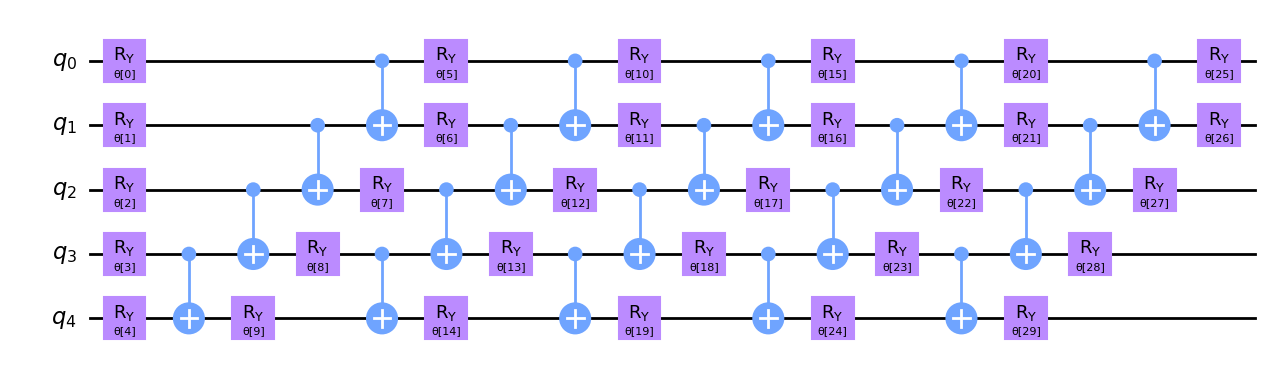
Ahora aplicamos este Codificador al estado que deseamos comprimir. En este ejemplo, dividimos nuestro estado inicial de \(5\) qubits en un estado latente de \(3\) qubits (\(n = 3\)) y un espacio basura de \(2\) qubits (\(k = 2\)).
Como se explicó en la sección anterior, también debemos incluir un espacio de referencia de \(2\) qubits en nuestro circuito, así como un qubit auxiliar para realizar la prueba swap entre los estados de referencia y basura. Por lo tanto, tendremos un total de \(2 + 3 + 2 + 1 = 8\) qubits y \(1\) registro clásico en nuestro circuito.
Después de inicializar nuestro estado, aplicamos nuestro circuito parametrizado.
Después de esto, dividimos nuestro estado inicial en el espacio latente (el estado comprimido) y el espacio basura (la parte del estado que descartaremos) y realizamos la prueba swap entre el estado de referencia y el espacio basura. Luego se mide el último qubit para determinar la fidelidad entre los estados de referencia y basura. Una representación pictórica de esto se da a continuación en la Figura 4.
Figura 4: Ejemplo de un Autocodificador Cuántico en proceso de entrenamiento. Usamos la prueba swap para determinar la fidelidad entre los espacios basura y de referencia.
Definimos una función a continuación para implementar la configuración del circuito anterior en el estado de pared de dominio \(|00111\rangle\) de \(5\) qubits y graficar un ejemplo a continuación. Aquí los qubits \(5\) y \(6\) son el estado de referencia, \(0, 1, 2, 3, 4\) son el estado inicial que deseamos comprimir y el qubit \(7\) es nuestro qubit auxiliar que se usa en la prueba swap. También incluimos un registro clásico para medir los resultados del qubit \(7\) en la prueba swap.
[4]:
def auto_encoder_circuit(num_latent, num_trash):
qr = QuantumRegister(num_latent + 2 * num_trash + 1, "q")
cr = ClassicalRegister(1, "c")
circuit = QuantumCircuit(qr, cr)
circuit.compose(ansatz(num_latent + num_trash), range(0, num_latent + num_trash), inplace=True)
circuit.barrier()
auxiliary_qubit = num_latent + 2 * num_trash
# swap test
circuit.h(auxiliary_qubit)
for i in range(num_trash):
circuit.cswap(auxiliary_qubit, num_latent + i, num_latent + num_trash + i)
circuit.h(auxiliary_qubit)
circuit.measure(auxiliary_qubit, cr[0])
return circuit
num_latent = 3
num_trash = 2
circuit = auto_encoder_circuit(num_latent, num_trash)
circuit.draw("mpl")
[4]:
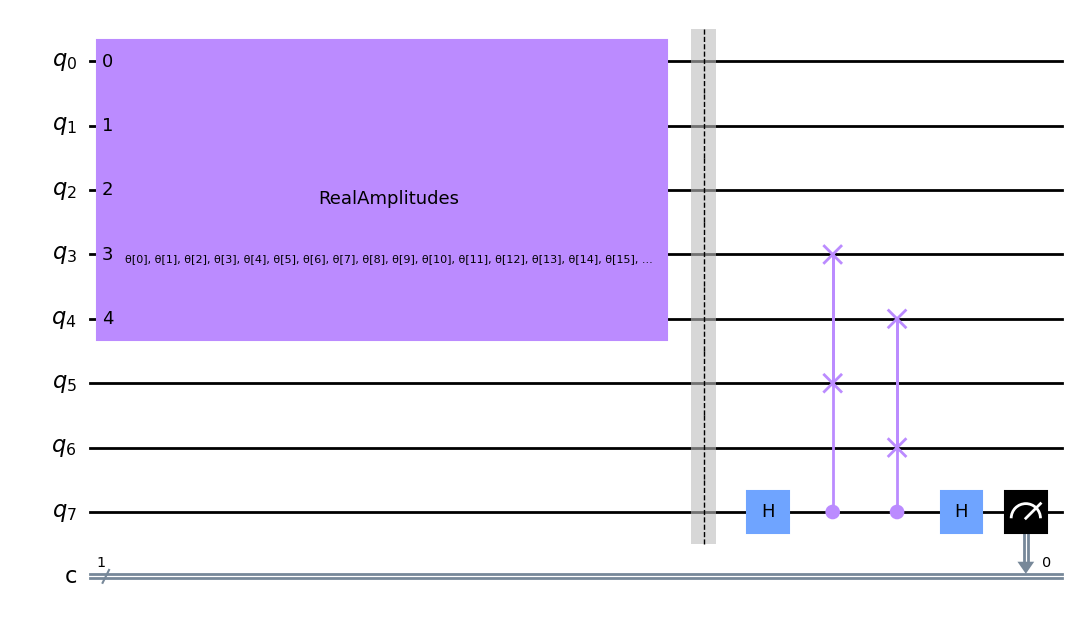
Para reconstruir el estado de entrada original, debemos aplicar el adjunto de nuestro circuito parametrizado después de la prueba swap. Sin embargo, durante el entrenamiento, solo nos interesa el estado basura y el estado de referencia. Por lo tanto, podemos excluir las compuertas que siguen a la compresión hasta que deseemos reconstruir nuestra entrada inicial.
Después de construir nuestro Autocodificador Cuántico, el siguiente paso es entrenarlo para comprimir el estado y maximizar la función de costo y determinar los parámetros \(\theta\).
6. Un Ejemplo Simple: El Autocodificador de la Pared de Dominio#
Comencemos primero con un ejemplo simple, un estado conocido como Pared de Dominio (Domain Wall), que para \(5\) qubits viene dado por \(|00111\rangle\). Aquí intentaremos comprimir este estado de \(5\) qubits a \(3\) qubits, con los qubits restantes en el espacio basura, en el estado \(|00\rangle\). Podemos crear una función para construir el estado de la pared de dominio a continuación.
[5]:
def domain_wall(circuit, a, b):
# Here we place the Domain Wall to qubits a - b in our circuit
for i in np.arange(int(b / 2), int(b)):
circuit.x(i)
return circuit
domain_wall_circuit = domain_wall(QuantumCircuit(5), 0, 5)
domain_wall_circuit.draw("mpl")
[5]:
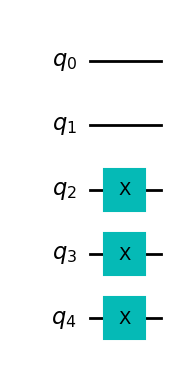
Ahora entrenemos nuestro Autocodificador para comprimir este estado de 5 qubits a 3 qubits (qubits 0,1 y 2), con los qubits restantes en el espacio basura (qubits 3 y 4) en el estado |00>.
Creamos un circuito para usar en la función de pérdida, como se describe en la Sección 4, que determina la fidelidad entre los dos estados a continuación usando la prueba swap para nuestra función particular de Autocodificador. Para obtener más información sobre la prueba swap, consulta [1].
[6]:
ae = auto_encoder_circuit(num_latent, num_trash)
qc = QuantumCircuit(num_latent + 2 * num_trash + 1, 1)
qc = qc.compose(domain_wall_circuit, range(num_latent + num_trash))
qc = qc.compose(ae)
qc.draw("mpl")
[6]:

Luego, creamos una red neuronal cuántica y pasamos el circuito como parámetro. Notamos que esta red debe tomar una función de interpretación, que determina cómo mapeamos la salida de la red a la forma de salida. Dado que medimos solo un qubit, la salida de la red es una cadena de bits, ya sea \(0\) o \(1\), por lo que la forma de salida es \(2\), el número de resultados posibles. Luego, introducimos un mapeo de identidad. La salida de la red es un vector de probabilidades de obtener cadenas de bits interpretadas. Por lo tanto, obtenemos las probabilidades de obtener \(0\) o \(1\) y esto es exactamente lo que estamos buscando. En la función de costo hacemos uso de la probabilidad de obtener \(1\) y penalizamos los resultados que llevan a \(1\), maximizando así la fidelidad entre el espacio basura y el espacio de referencia.
[7]:
# Here we define our interpret for our SamplerQNN
def identity_interpret(x):
return x
qnn = SamplerQNN(
circuit=qc,
input_params=[],
weight_params=ae.parameters,
interpret=identity_interpret,
output_shape=2,
)
A continuación, creamos nuestra función de costo. Como se describe en la sección anterior, nuestro objetivo es minimizar \(\frac{2}{M}L\), que es el doble de probabilidad de obtener el qubit final en el estado \(|1\rangle\). Por lo tanto, deseamos minimizar la posibilidad de obtener un \(|1\rangle\) en el qubit 7.
La función de costo también graficará el valor objetivo en cada evaluación de la función de costo.
[8]:
def cost_func_domain(params_values):
probabilities = qnn.forward([], params_values)
# we pick a probability of getting 1 as the output of the network
cost = np.sum(probabilities[:, 1])
# plotting part
clear_output(wait=True)
objective_func_vals.append(cost)
plt.title("Objective function value against iteration")
plt.xlabel("Iteration")
plt.ylabel("Objective function value")
plt.plot(range(len(objective_func_vals)), objective_func_vals)
plt.show()
return cost
Ahora entrenaremos nuestro Autocodificador para reducir la dimensión del espacio de Hilbert de \(5\) qubits a \(3\), dejando el espacio basura en el estado \(|00\rangle\). Inicialmente, establecemos los parámetros \(\theta\) en valores aleatorios y ajustamos estos parámetros para minimizar nuestra función de costo mediante el uso del optimizador COBYLA.
[9]:
opt = COBYLA(maxiter=150)
initial_point = algorithm_globals.random.random(ae.num_parameters)
objective_func_vals = []
# make the plot nicer
plt.rcParams["figure.figsize"] = (12, 6)
start = time.time()
opt_result = opt.minimize(cost_func_domain, initial_point)
elapsed = time.time() - start
print(f"Fit in {elapsed:0.2f} seconds")
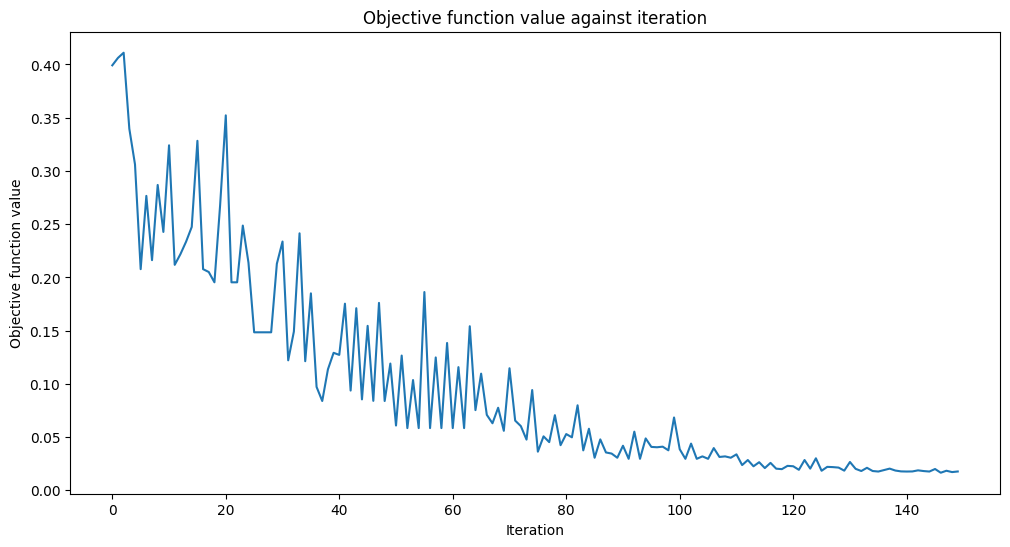
Fit in 18.48 seconds
¡Parece que ha convergido! Después de entrenar nuestro Autocodificador Cuántico, ¡construyámoslo y veamos qué tan bien comprime el estado!
Para hacer esto, primero aplicamos nuestro autocodificador a un estado de pared de dominio de \(5\) qubits. Después de aplicar este estado, el estado comprimido debe tener la forma \(|00\rangle\). Por lo tanto, restablecer los dos últimos qubits no debería afectar a nuestro estado general.
Después de restablecer, aplicamos nuestro decodificador (el conjugado hermitiano de nuestro codificador) y lo comparamos con el estado inicial determinando la fidelidad. Si nuestra fidelidad es uno, entonces nuestro Autocodificador ha codificado toda la información de la pared de dominio de manera eficiente en un conjunto más pequeño de qubits y al decodificar, ¡retenemos el estado original!
Primero apliquemos nuestro circuito al estado de la pared de dominio, utilizando los parámetros que obtuvimos al entrenar nuestro Autocodificador Cuántico. (Ten en cuenta que hemos incluido barreras en nuestro circuito a continuación, sin embargo, estas no son necesarias para la implementación del Autocodificador Cuántico y se utilizan para determinar las diferentes secciones de nuestro circuito).
[10]:
test_qc = QuantumCircuit(num_latent + num_trash)
test_qc = test_qc.compose(domain_wall_circuit)
ansatz_qc = ansatz(num_latent + num_trash)
test_qc = test_qc.compose(ansatz_qc)
test_qc.barrier()
test_qc.reset(4)
test_qc.reset(3)
test_qc.barrier()
test_qc = test_qc.compose(ansatz_qc.inverse())
test_qc.draw("mpl")
[10]:
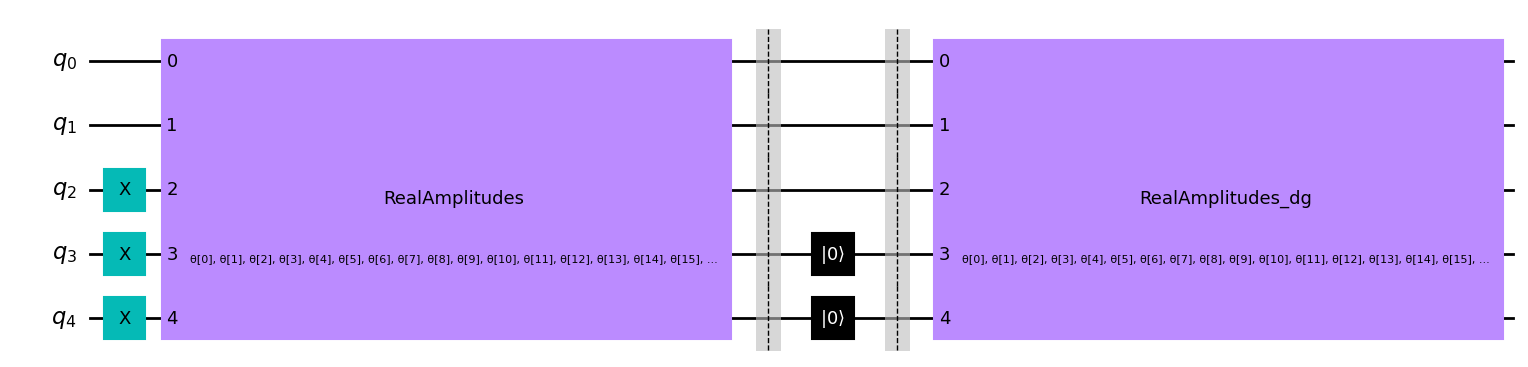
Ahora asignamos los valores de los parámetros obtenidos en el entrenamiento.
[11]:
test_qc = test_qc.assign_parameters(opt_result.x)
¡Ahora obtengamos los vectores de estado de nuestro circuito de salida y estado de la Pared de Dominio y calculemos la fidelidad!
[12]:
domain_wall_state = Statevector(domain_wall_circuit).data
output_state = Statevector(test_qc).data
fidelity = np.sqrt(np.dot(domain_wall_state.conj(), output_state) ** 2)
print("Fidelity of our Output State with our Input State: ", fidelity.real)
Fidelity of our Output State with our Input State: 0.9832814006314854
Como puedes ver, nuestra fidelidad es bastante alta y, por lo tanto, nuestro autocodificador ha comprimido nuestro conjunto de datos mientras ¡retiene toda la información del estado de entrada!
Ahora veremos si podemos aplicar dicho Autocodificador Cuántico a conjuntos de datos más complicados que contienen ruido, como imágenes de los números cero y uno.
7. Un Autocodificador Cuántico para Compresión Digital#
También se puede aplicar un Autocodificador Cuántico a ejemplos más complicados, como un conjunto de dígitos escritos a mano para comprimir el conjunto de datos. A continuación, mostraremos que, de hecho, podemos entrenar un Autocodificador Cuántico para comprimir un ejemplo de este tipo, lo que nos brinda la capacidad de almacenar datos de manera más eficiente en una computadora cuántica.
Para este tutorial, crearemos un Autocodificador Cuántico para un conjunto de datos ruidoso que contiene ceros y unos, que se puede ver a continuación.
Cada imagen contiene \(32\) pixeles de los cuales se pueden codificar en \(5\) qubits mediante la Codificación de Amplitud (Amplitude Encoding). Esto se puede hacer usando el mapa de características RawFeatureVector de Qiskit Machine Learning.
[13]:
def zero_idx(j, i):
# Index for zero pixels
return [
[i, j],
[i - 1, j - 1],
[i - 1, j + 1],
[i - 2, j - 1],
[i - 2, j + 1],
[i - 3, j - 1],
[i - 3, j + 1],
[i - 4, j - 1],
[i - 4, j + 1],
[i - 5, j],
]
def one_idx(i, j):
# Index for one pixels
return [[i, j - 1], [i, j - 2], [i, j - 3], [i, j - 4], [i, j - 5], [i - 1, j - 4], [i, j]]
def get_dataset_digits(num, draw=True):
# Create Dataset containing zero and one
train_images = []
train_labels = []
for i in range(int(num / 2)):
# First we introduce background noise
empty = np.array([algorithm_globals.random.uniform(0, 0.1) for i in range(32)]).reshape(
8, 4
)
# Now we insert the pixels for the one
for i, j in one_idx(2, 6):
empty[j][i] = algorithm_globals.random.uniform(0.9, 1)
train_images.append(empty)
train_labels.append(1)
if draw:
plt.title("This is a One")
plt.imshow(train_images[-1])
plt.show()
for i in range(int(num / 2)):
empty = np.array([algorithm_globals.random.uniform(0, 0.1) for i in range(32)]).reshape(
8, 4
)
# Now we insert the pixels for the zero
for k, j in zero_idx(2, 6):
empty[k][j] = algorithm_globals.random.uniform(0.9, 1)
train_images.append(empty)
train_labels.append(0)
if draw:
plt.imshow(train_images[-1])
plt.title("This is a Zero")
plt.show()
train_images = np.array(train_images)
train_images = train_images.reshape(len(train_images), 32)
for i in range(len(train_images)):
sum_sq = np.sum(train_images[i] ** 2)
train_images[i] = train_images[i] / np.sqrt(sum_sq)
return train_images, train_labels
train_images, __ = get_dataset_digits(2)
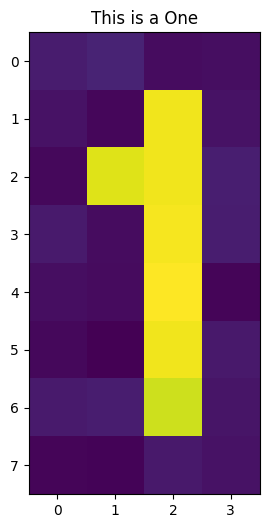
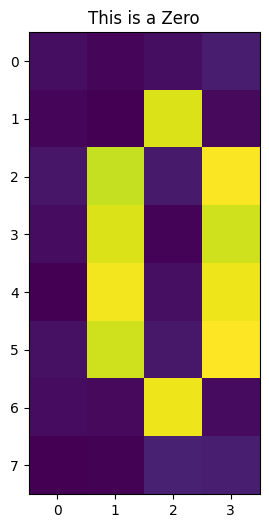
Después de codificar nuestra imagen en \(5\) qubits, comenzamos a entrenar nuestro Autocodificador Cuántico para comprimir este estado en \(3\) qubits.
Repetimos los pasos del ejemplo anterior y escribimos una función de costo, nuevamente basada en la Prueba Swap entre los espacios basura y latente. También podemos usar la misma función de Autocodificador que se proporciona en el ejemplo anterior, ya que el estado de entrada y el espacio basura contienen la misma cantidad de qubits.
Ingresemos uno de nuestros dígitos y veamos nuestro circuito para el Autocodificador a continuación.
[14]:
num_latent = 3
num_trash = 2
fm = RawFeatureVector(2 ** (num_latent + num_trash))
ae = auto_encoder_circuit(num_latent, num_trash)
qc = QuantumCircuit(num_latent + 2 * num_trash + 1, 1)
qc = qc.compose(fm, range(num_latent + num_trash))
qc = qc.compose(ae)
qc.draw("mpl")
[14]:

Nuevamente, podemos ver la prueba swap que se realiza en los qubits \(3\), \(4\), \(5\) y \(6\), que determinarán el valor de nuestra función de costo.
[15]:
def identity_interpret(x):
return x
qnn = SamplerQNN(
circuit=qc,
input_params=fm.parameters,
weight_params=ae.parameters,
interpret=identity_interpret,
output_shape=2,
)
Construimos nuestra función de costo, basada en la prueba swap entre los espacios de referencia y basura para el conjunto de datos de dígitos. Para hacer esto, nuevamente usamos la red CircuitQNN de Qiskit Machine Learning y usamos la misma función de interpretación ya que estamos midiendo la probabilidad de obtener el qubit final en el estado \(|1\rangle\).
[16]:
def cost_func_digits(params_values):
probabilities = qnn.forward(train_images, params_values)
cost = np.sum(probabilities[:, 1]) / train_images.shape[0]
# plotting part
clear_output(wait=True)
objective_func_vals.append(cost)
plt.title("Objective function value against iteration")
plt.xlabel("Iteration")
plt.ylabel("Objective function value")
plt.plot(range(len(objective_func_vals)), objective_func_vals)
plt.show()
return cost
Dado que el entrenamiento del modelo puede llevar mucho tiempo, ya hemos entrenado previamente el modelo para algunas iteraciones y hemos guardado los pesos previamente entrenados. Continuaremos entrenando desde ese punto configurando initial_point a un vector de pesos preentrenados.
[17]:
with open("12_qae_initial_point.json", "r") as f:
initial_point = json.load(f)
Al minimizar esta función de costo, podemos determinar los parámetros necesarios para comprimir nuestras imágenes ruidosas. ¡Veamos si podemos codificar nuestras imágenes!
[18]:
opt = COBYLA(maxiter=150)
objective_func_vals = []
# make the plot nicer
plt.rcParams["figure.figsize"] = (12, 6)
start = time.time()
opt_result = opt.minimize(fun=cost_func_digits, x0=initial_point)
elapsed = time.time() - start
print(f"Fit in {elapsed:0.2f} seconds")
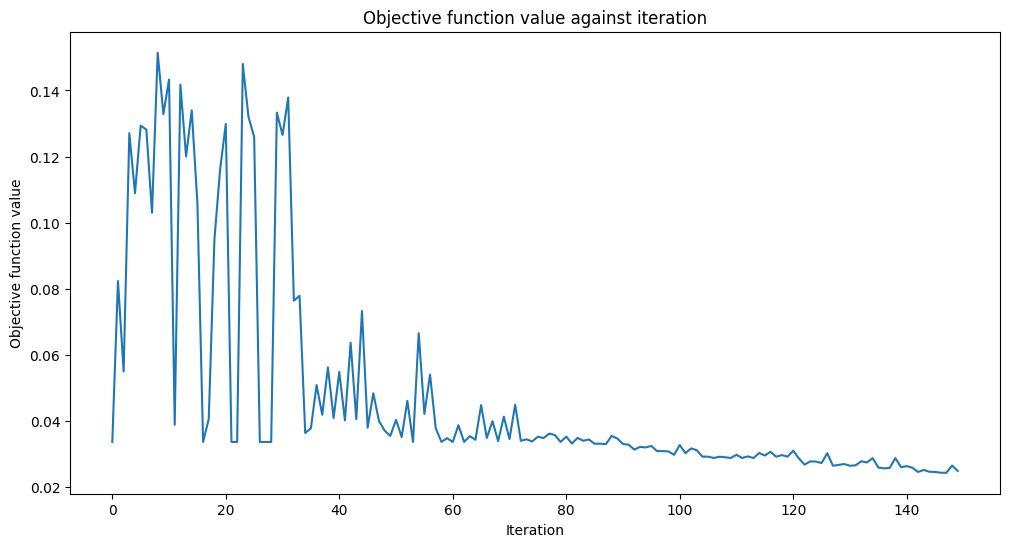
Fit in 40.59 seconds
¡Parece que ha convergido!
Ahora construyamos nuestro Codificador y Decodificador usando los parámetros obtenidos del periodo de entrenamiento. Después de aplicar este circuito a nuestro nuevo conjunto de datos, podemos comparar nuestros datos de entrada y salida y ¡ver si pudimos retener las imágenes de manera eficiente durante la compresión!
[19]:
# Test
test_qc = QuantumCircuit(num_latent + num_trash)
test_qc = test_qc.compose(fm)
ansatz_qc = ansatz(num_latent + num_trash)
test_qc = test_qc.compose(ansatz_qc)
test_qc.barrier()
test_qc.reset(4)
test_qc.reset(3)
test_qc.barrier()
test_qc = test_qc.compose(ansatz_qc.inverse())
# sample new images
test_images, test_labels = get_dataset_digits(2, draw=False)
for image, label in zip(test_images, test_labels):
original_qc = fm.assign_parameters(image)
original_sv = Statevector(original_qc).data
original_sv = np.reshape(np.abs(original_sv) ** 2, (8, 4))
param_values = np.concatenate((image, opt_result.x))
output_qc = test_qc.assign_parameters(param_values)
output_sv = Statevector(output_qc).data
output_sv = np.reshape(np.abs(output_sv) ** 2, (8, 4))
fig, (ax1, ax2) = plt.subplots(1, 2)
ax1.imshow(original_sv)
ax1.set_title("Input Data")
ax2.imshow(output_sv)
ax2.set_title("Output Data")
plt.show()
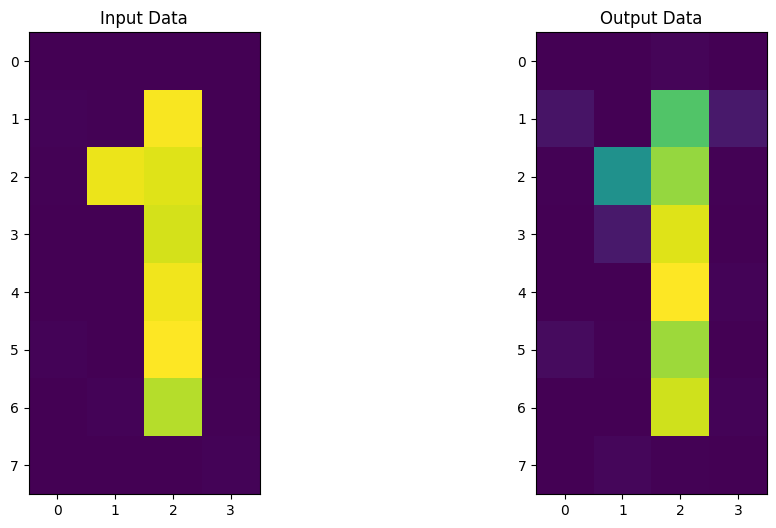
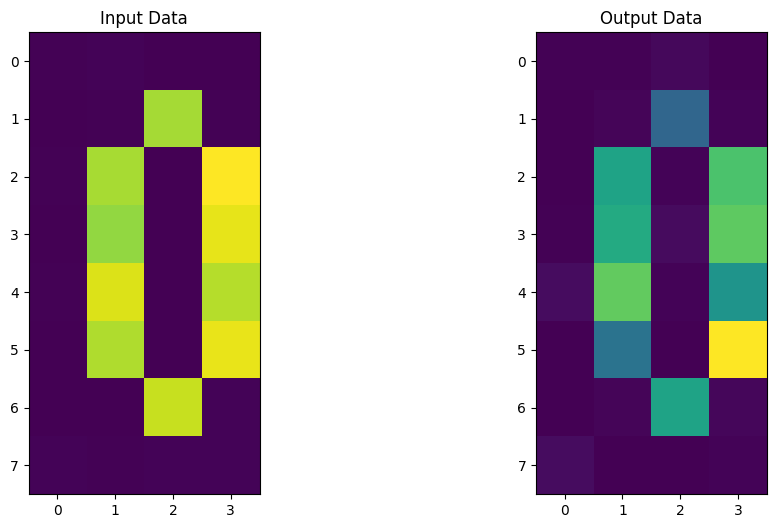
¡Parece que nuestro Autocodificador Cuántico también se puede entrenar para codificar dígitos! ¡Ahora es tu turno de construir tu propio Autocodificador Cuántico y generar ideas y conjuntos de datos a comprimir!
8. Aplicaciones de un Autocodificador Cuántico#
El Autocodificador Cuántico se puede usar para varias aplicaciones diferentes, que incluyen
Compresión digital: donde la información se puede codificar en una cantidad menor de qubits. Esto puede ser muy beneficioso para los dispositivos cuánticos de término cercano, ya que los sistemas de qubits más pequeños son menos propensos al ruido.
Eliminación de ruido: donde se puede usar Autocodificación Cuántica para extraer características relevantes del estado cuántico inicial o datos codificados, mientras se ignora cualquier ruido adicional.
Química Cuántica: en la que se puede utilizar un Autocodificador Cuántico como ansatz para sistemas, como el Modelo Hubbard. Esto se usa comúnmente para describir las interacciones electrón-electrón en las moléculas.
9. Referencias#
Una página de wikipedia sobre el Autocodificador: https://en.wikipedia.org/wiki/Autoencoder
Romero, Jonathan, Jonathan P. Olson, and Alan Aspuru-Guzik. «Quantum autoencoders for efficient compression of quantum data.» Quantum Science and Technology 2.4 (2017): 045001.
Algoritmo de la Prueba de Swap: https://en.wikipedia.org/wiki/Swap_test
[20]:
import qiskit.tools.jupyter
%qiskit_version_table
%qiskit_copyright
Version Information
| Qiskit Software | Version |
|---|---|
qiskit-terra | 0.22.2 |
qiskit-aer | 0.11.1 |
qiskit-machine-learning | 0.6.0 |
| System information | |
| Python version | 3.8.13 |
| Python compiler | Clang 12.0.0 |
| Python build | default, Oct 19 2022 17:54:22 |
| OS | Darwin |
| CPUs | 10 |
| Memory (Gb) | 64.0 |
| Thu Nov 10 23:26:05 2022 GMT | |
This code is a part of Qiskit
© Copyright IBM 2017, 2022.
This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.