Error analysis¶
Mitigating readout errors does not come for free. Instead, there is an overhaed that results in increased uncertainty in the computed results. M3 will optionally compute this overhead and return an upper-bound on the expected standard deviation (variance) of the computed expectation values.
Let us first calibrate the mitigator and get raw results:
from qiskit import *
from qiskit.providers.fake_provider import FakeCasablanca
import mthree
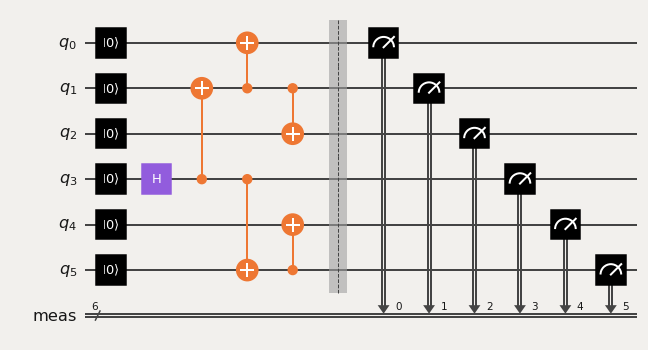
qc = QuantumCircuit(6)
qc.reset(range(6))
qc.h(3)
qc.cx(3,1)
qc.cx(3,5)
qc.cx(1,0)
qc.cx(5,4)
qc.cx(1,2)
qc.measure_all()
qc.draw('mpl')
backend = FakeCasablanca()
mit = mthree.M3Mitigation(backend)
mit.cals_from_system(range(6))
trans_qc = transpile(qc, backend)
raw_counts = backend.run(trans_qc, shots=8192).result().get_counts()
In order to compute the standard deviation of out mitigated expectation values we need to request the information be computed:
quasis = mit.apply_correction(raw_counts, range(6), return_mitigation_overhead=True)
The mitigation overhead is returned as an attribute of the returned quasi-probabilites
quasis.mitigation_overhead
1.7543186068158614
that, together with the number of shots taken, determines the upper-bound on the standard deviation:
quasis.stddev()
0.014633872370585197
It is also possible to return both the expectation value and standard deviation in a single call:
quasis.expval_and_stddev()
(0.913253158241035, 0.014633872370585197)
Although this standard deviation is an upper-bound, it is usually a tight upper-bound that can be faithfully used futher analysis.