Note

This page was generated from docs/tutorials/03_minimum_eigen_optimizer.ipynb.

Minimum Eigen Optimizer

Introduction

An interesting class of optimization problems to be addressed by quantum computing are Quadratic Unconstrained Binary Optimization (QUBO) problems. Finding the solution to a QUBO is equivalent to finding the ground state of a corresponding Ising Hamiltonian, which is an important problem not only in optimization, but also in quantum chemistry and physics. For this translation, the binary variables taking values in \(\{0, 1\}\) are replaced by spin variables taking values in \(\{-1, +1\}\), which allows one to replace the resulting spin variables by Pauli Z matrices, and thus, an Ising Hamiltonian. For more details on this mapping we refer to [1].

Qiskit provides automatic conversion from a suitable QuadraticProgram to an Ising Hamiltonian, which then allows leveraging all the SamplingMinimumEigensolver implementations, such as

• SamplingVQE,

• QAOA, or

• NumpyMinimumEigensolver (classical exact method).

Note 1: MinimumEigenOptimizer does not support qiskit.algorithms.minimum_eigensolver.VQE. But qiskit.algorithms.minimum_eigensolver.SamplingVQE can be used instead.

Note 2: MinimumEigenOptimizer can use NumpyMinimumEigensolver as an exception case though it inherits MinimumEigensolver (not SamplingMinimumEigensolver).

Qiskit Optimization provides a the MinimumEigenOptimizer class, which wraps the translation to an Ising Hamiltonian (in Qiskit Terra also called Operator), the call to a MinimumEigensolver, and the translation of the results back to an OptimizationResult.

In the following we first illustrate the conversion from a QuadraticProgram to an Operator and then show how to use the MinimumEigenOptimizer with different MinimumEigensolvers to solve a given QuadraticProgram. The algorithms in Qiskit automatically try to convert a given problem to the supported problem class if possible, for instance, the MinimumEigenOptimizer will automatically translate integer variables to binary variables or add linear equality constraints as a quadratic penalty term to the objective. It should be mentioned that a QiskitOptimizationError will be thrown if conversion of a quadratic program with integer variables is attempted.

The circuit depth of QAOA potentially has to be increased with the problem size, which might be prohibitive for near-term quantum devices. A possible workaround is Recursive QAOA, as introduced in [2]. Qiskit generalizes this concept to the RecursiveMinimumEigenOptimizer, which is introduced at the end of this tutorial.

References

[1] A. Lucas, Ising formulations of many NP problems, Front. Phys., 12 (2014).

[2] S. Bravyi, A. Kliesch, R. Koenig, E. Tang, Obstacles to State Preparation and Variational Optimization from Symmetry Protection, arXiv preprint arXiv:1910.08980 (2019).

Converting a QUBO to an Operator

from qiskit.utils import algorithm_globals
from qiskit.algorithms.minimum_eigensolvers import QAOA, NumPyMinimumEigensolver
from qiskit.algorithms.optimizers import COBYLA
from qiskit.primitives import Sampler
from qiskit_optimization.algorithms import (
    MinimumEigenOptimizer,
    RecursiveMinimumEigenOptimizer,
    SolutionSample,
    OptimizationResultStatus,
)
from qiskit_optimization import QuadraticProgram
from qiskit.visualization import plot_histogram
from typing import List, Tuple
import numpy as np

# create a QUBO
qubo = QuadraticProgram()
qubo.binary_var("x")
qubo.binary_var("y")
qubo.binary_var("z")
qubo.minimize(linear=[1, -2, 3], quadratic={("x", "y"): 1, ("x", "z"): -1, ("y", "z"): 2})
print(qubo.prettyprint())

Problem name:

Minimize
  x*y - x*z + 2*y*z + x - 2*y + 3*z

Subject to
  No constraints

  Binary variables (3)
    x y z

Next we translate this QUBO into an Ising operator. This results not only in an Operator but also in a constant offset to be taken into account to shift the resulting value.

op, offset = qubo.to_ising()
print("offset: {}".format(offset))
print("operator:")
print(op)

offset: 1.5
operator:
-0.5 * IIZ
+ 0.25 * IZI
- 1.75 * ZII
+ 0.25 * IZZ
- 0.25 * ZIZ
+ 0.5 * ZZI

Sometimes a QuadraticProgram might also directly be given in the form of an Operator. For such cases, Qiskit also provides a translator from an Operator back to a QuadraticProgram, which we illustrate in the following.

qp = QuadraticProgram()
qp.from_ising(op, offset, linear=True)
print(qp.prettyprint())

Problem name:

Minimize
  x0*x1 - x0*x2 + 2*x1*x2 + x0 - 2*x1 + 3*x2

Subject to
  No constraints

  Binary variables (3)
    x0 x1 x2

This translator allows, for instance, one to translate an Operator to a QuadraticProgram and then solve the problem with other algorithms that are not based on the Ising Hamiltonian representation, such as the GroverOptimizer.

Solving a QUBO with the MinimumEigenOptimizer

We start by initializing the MinimumEigensolver we want to use.

algorithm_globals.random_seed = 10598
qaoa_mes = QAOA(sampler=Sampler(), optimizer=COBYLA(), initial_point=[0.0, 0.0])
exact_mes = NumPyMinimumEigensolver()

Then, we use the MinimumEigensolver to create MinimumEigenOptimizer.

qaoa = MinimumEigenOptimizer(qaoa_mes)  # using QAOA
exact = MinimumEigenOptimizer(exact_mes)  # using the exact classical numpy minimum eigen solver

We first use the MinimumEigenOptimizer based on the classical exact NumPyMinimumEigensolver to get the optimal benchmark solution for this small example.

exact_result = exact.solve(qubo)
print(exact_result.prettyprint())

objective function value: -2.0
variable values: x=0.0, y=1.0, z=0.0
status: SUCCESS

Next we apply the MinimumEigenOptimizer based on QAOA to the same problem.

qaoa_result = qaoa.solve(qubo)
print(qaoa_result.prettyprint())

objective function value: -2.0
variable values: x=0.0, y=1.0, z=0.0
status: SUCCESS

Analysis of Samples

OptimizationResult provides useful information in the form of SolutionSamples (here denoted as samples). Each SolutionSample contains information about the input values (x), the corresponding objective function value (fval), the fraction of samples corresponding to that input (probability), and the solution status (SUCCESS, FAILURE, INFEASIBLE). Multiple samples corresponding to the same input are consolidated into a single SolutionSample (with its probability attribute being the aggregate fraction of samples represented by that SolutionSample).

print("variable order:", [var.name for var in qaoa_result.variables])
for s in qaoa_result.samples:
    print(s)

variable order: ['x', 'y', 'z']
SolutionSample(x=array([0., 1., 0.]), fval=-2.0, probability=0.4410900880690431, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([0., 0., 0.]), fval=0.0, probability=0.2276092830372722, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([1., 1., 0.]), fval=0.0, probability=0.1413052418997499, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([1., 0., 0.]), fval=1.0, probability=0.1257222100828826, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([0., 0., 1.]), fval=3.0, probability=0.0205255745635282, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([1., 0., 1.]), fval=3.0, probability=0.03044357461683, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([0., 1., 1.]), fval=3.0, probability=0.0123872794392166, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([1., 1., 1.]), fval=4.0, probability=0.0009167482914771, status=<OptimizationResultStatus.SUCCESS: 0>)

We may also want to filter samples according to their status or probabilities.

def get_filtered_samples(
    samples: List[SolutionSample],
    threshold: float = 0,
    allowed_status: Tuple[OptimizationResultStatus] = (OptimizationResultStatus.SUCCESS,),
):
    res = []
    for s in samples:
        if s.status in allowed_status and s.probability > threshold:
            res.append(s)

    return res

filtered_samples = get_filtered_samples(
    qaoa_result.samples, threshold=0.005, allowed_status=(OptimizationResultStatus.SUCCESS,)
)
for s in filtered_samples:
    print(s)

SolutionSample(x=array([0., 1., 0.]), fval=-2.0, probability=0.4410900880690431, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([0., 0., 0.]), fval=0.0, probability=0.2276092830372722, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([1., 1., 0.]), fval=0.0, probability=0.1413052418997499, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([1., 0., 0.]), fval=1.0, probability=0.1257222100828826, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([0., 0., 1.]), fval=3.0, probability=0.0205255745635282, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([1., 0., 1.]), fval=3.0, probability=0.03044357461683, status=<OptimizationResultStatus.SUCCESS: 0>)
SolutionSample(x=array([0., 1., 1.]), fval=3.0, probability=0.0123872794392166, status=<OptimizationResultStatus.SUCCESS: 0>)

If we want to obtain a better perspective of the results, statistics is very helpful, both with respect to the objective function values and their respective probabilities. Thus, mean and standard deviation are the very basics for understanding the results.

fvals = [s.fval for s in qaoa_result.samples]
probabilities = [s.probability for s in qaoa_result.samples]

np.mean(fvals)

1.5

np.std(fvals)

1.9364916731037085

Finally, despite all the number-crunching, visualization is usually the best early-analysis approach.

samples_for_plot = {
    " ".join(f"{qaoa_result.variables[i].name}={int(v)}" for i, v in enumerate(s.x)): s.probability
    for s in filtered_samples
}
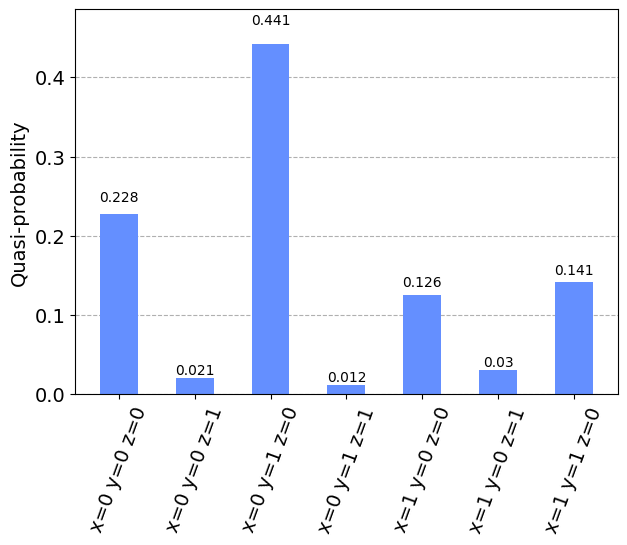
samples_for_plot

{'x=0 y=1 z=0': 0.4410900880690431,
 'x=0 y=0 z=0': 0.2276092830372722,
 'x=1 y=1 z=0': 0.1413052418997499,
 'x=1 y=0 z=0': 0.1257222100828826,
 'x=0 y=0 z=1': 0.0205255745635282,
 'x=1 y=0 z=1': 0.03044357461683,
 'x=0 y=1 z=1': 0.0123872794392166}

plot_histogram(samples_for_plot)

RecursiveMinimumEigenOptimizer

The RecursiveMinimumEigenOptimizer takes a MinimumEigenOptimizer as input and applies the recursive optimization scheme to reduce the size of the problem one variable at a time. Once the size of the generated intermediate problem is below a given threshold (min_num_vars), the RecursiveMinimumEigenOptimizer uses another solver (min_num_vars_optimizer), e.g., an exact classical solver such as CPLEX or the MinimumEigenOptimizer based on the NumPyMinimumEigensolver.

In the following, we show how to use the RecursiveMinimumEigenOptimizer using the two MinimumEigenOptimizers introduced before.

First, we construct the RecursiveMinimumEigenOptimizer such that it reduces the problem size from 3 variables to 1 variable and then uses the exact solver for the last variable. Then we call solve to optimize the considered problem.

rqaoa = RecursiveMinimumEigenOptimizer(qaoa, min_num_vars=1, min_num_vars_optimizer=exact)

rqaoa_result = rqaoa.solve(qubo)
print(rqaoa_result.prettyprint())

objective function value: -2.0
variable values: x=0.0, y=1.0, z=0.0
status: SUCCESS

filtered_samples = get_filtered_samples(
    rqaoa_result.samples, threshold=0.005, allowed_status=(OptimizationResultStatus.SUCCESS,)
)

samples_for_plot = {
    " ".join(f"{rqaoa_result.variables[i].name}={int(v)}" for i, v in enumerate(s.x)): s.probability
    for s in filtered_samples
}
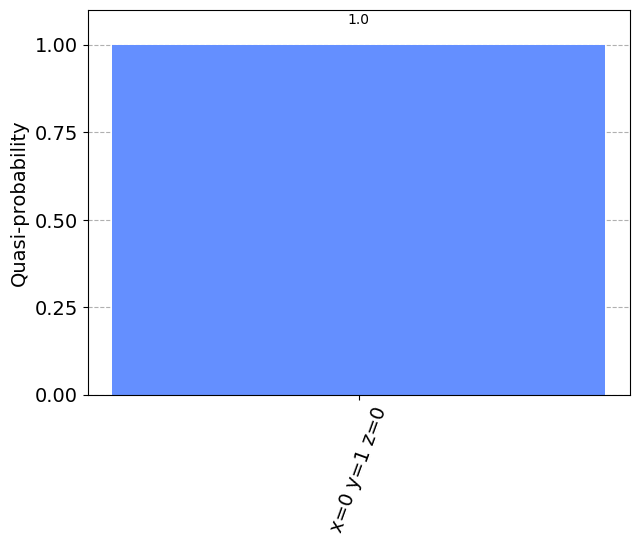
samples_for_plot

{'x=0 y=1 z=0': 1.0}

plot_histogram(samples_for_plot)

import qiskit.tools.jupyter

%qiskit_version_table
%qiskit_copyright

Version Information

Qiskit Software	Version
qiskit-terra	0.24.0
qiskit-aer	0.12.0
qiskit-optimization	0.5.0
System information
Python version	3.8.16
Python compiler	GCC 11.3.0
Python build	default, Jan 11 2023 00:28:51
OS	Linux
CPUs	2
Memory (Gb)	6.781208038330078
Wed May 10 12:47:27 2023 UTC

This code is a part of Qiskit

© Copyright IBM 2017, 2023.

This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.

Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.