Nota

Esta página fue generada a partir de docs/tutorials/09_application_classes.ipynb.

Clases de Aplicación para Problemas de Optimización#

Introducción#

Introducimos clases de aplicaciones para los siguientes problemas de optimización para que los usuarios puedan probar fácilmente varios problemas de optimización en computadoras cuánticas.

Problema de cobertura exacta

Dada una colección de subconjuntos de elementos, encuentra una subcolección tal que cada elemento se cubra exactamente una vez.

Problema de la mochila (knapsack)

Dado un conjunto de elementos, encuentra un subconjunto de elementos de modo que el peso total esté dentro de la capacidad y el valor total sea maximizado.

Problema de partición de números

Dado un conjunto múltiple de enteros positivos, encuentra una partición del conjunto múltiple en dos subconjuntos de modo que las sumas de los subconjuntos sean iguales.

Problema del empaquetamiento de conjuntos

Dada una colección de subconjuntos de elementos, encuentra una subcolección tal que todos los subconjuntos de la subcolección estén separados por pares y se maximice el número de elementos de la subcolección.

Problemas con grafos

Problema del clan (clique)

Dado un grafo no dirigido, encuentra un subconjunto de nodos con un número especificado o el número máximo de modo que el subgrafo inducido esté completo.

Problema de partición de grafos

Dado un grafo no dirigido, encuentra una partición en dos componentes cuyos tamaños sean iguales de tal manera que la capacidad total de las aristas entre los dos componentes sea mínima.

Problema de máximo corte (max-cut)

Dado un grafo no dirigido, encuentra una partición de nodos en dos subconjuntos de modo que se maximice el peso total de las aristas entre los dos subconjuntos.

Problema del conjunto estable

Dado un grafo no dirigido, encuentra un subconjunto de nodos de modo que ninguna arista conecte los nodos en el subconjunto y se maximice el número de nodos.

Problema del vendedor viajero

Dado un grafo, encuentra una ruta con la distancia mínima tal que la ruta visite cada ciudad exactamente una vez.

Problema de las rutas de vehículos

Dado un grafo, un nodo depósito y el número de vehículos (rutas), encuentra un conjunto de rutas de modo que cada nodo se cubra exactamente una vez, excepto el depósito, y la distancia total de las rutas sea minimizada.

Problema da la cobertura de vértices

Dado un grafo no dirigido, encuentra un subconjunto de nodos con el tamaño mínimo tal que cada arista tenga al menos un punto final en los subconjuntos.

Las clases de aplicaciones para problemas de grafos (GraphOptimizationApplication) proporcionan una funcionalidad para dibujar los grafos de una instancia y un resultado. Ten en cuenta que debes instalar matplotlib de antemano para utilizar la funcionalidad.

Introducimos ejemplos del problema de la cobertura de vértices y el problema de la mochila (knapsack) en esta página.

Ejemplos del problema max-cut y el problema del vendedor viajero están disponibles en Max-Cut y Problema del Vendedor Viajero.

Primero importamos los paquetes necesarios para las clases de aplicaciones.

[1]:

from qiskit_optimization.algorithms import MinimumEigenOptimizer
from qiskit_algorithms.utils import algorithm_globals
from qiskit_algorithms import QAOA, NumPyMinimumEigensolver
from qiskit_algorithms.optimizers import COBYLA
from qiskit.primitives import Sampler

Problema da la cobertura de vértices#

Introducimos la clase de aplicación para el problema de cobertura de vértices como un ejemplo de problemas de grafos. Dado un grafo no dirigido, el problema de la cobertura de vértices nos pide que busquemos un subconjunto de nodos con el tamaño mínimo tal que todas las aristas estén cubiertas por cualquier nodo seleccionado.

Importamos la clase de aplicación VertexCover para el problema de cobertura de vértices y networkx para generar un grafo aleatorio.

[2]:

from qiskit_optimization.applications.vertex_cover import VertexCover
import networkx as nx

seed = 123
algorithm_globals.random_seed = seed

[3]:

graph = nx.random_regular_graph(d=3, n=6, seed=seed)
pos = nx.spring_layout(graph, seed=seed)

[4]:

prob = VertexCover(graph)
prob.draw(pos=pos)

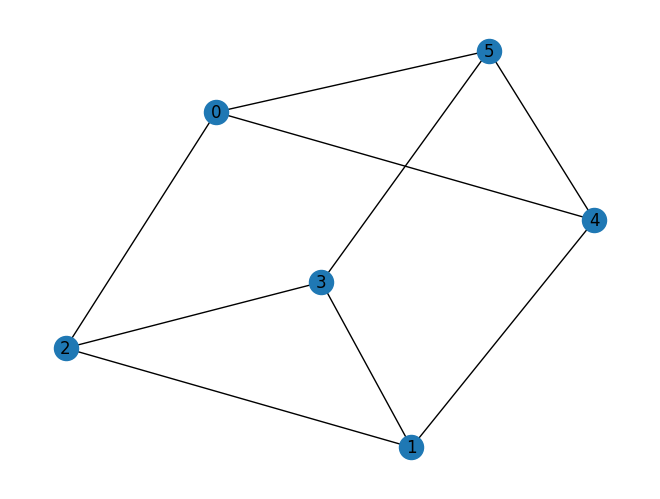
../_images/tutorials_09_application_classes_8_0.png

VertexCover toma un grafo como instancia y to_quadratic_program genera un correspondiente QuadraticProgram de la instancia del problema de cobertura de vértices.

[5]:

qp = prob.to_quadratic_program()
print(qp.prettyprint())

Problem name: Vertex cover

Minimize
  x_0 + x_1 + x_2 + x_3 + x_4 + x_5

Subject to
  Linear constraints (9)
    x_1 + x_2 >= 1  'c0'
    x_1 + x_4 >= 1  'c1'
    x_1 + x_3 >= 1  'c2'
    x_2 + x_3 >= 1  'c3'
    x_0 + x_2 >= 1  'c4'
    x_0 + x_4 >= 1  'c5'
    x_0 + x_5 >= 1  'c6'
    x_4 + x_5 >= 1  'c7'
    x_3 + x_5 >= 1  'c8'

  Binary variables (6)
    x_0 x_1 x_2 x_3 x_4 x_5

Puedes resolver el problema de la siguiente manera. NumPyMinimumEigensolver encuentra el vector propio mínimo. También puedes aplicar QAOA. Ten en cuenta que la solución de QAOA no siempre es óptima.

[6]:

# Numpy Eigensolver
meo = MinimumEigenOptimizer(min_eigen_solver=NumPyMinimumEigensolver())
result = meo.solve(qp)
print(result.prettyprint())
print("\nsolution:", prob.interpret(result))
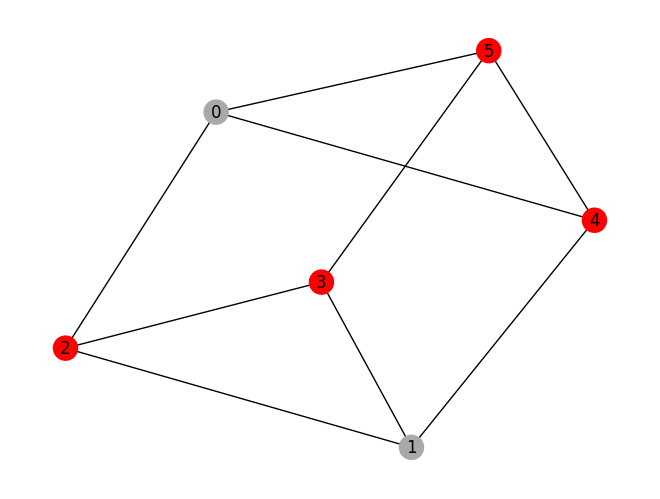
prob.draw(result, pos=pos)

objective function value: 4.0
variable values: x_0=0.0, x_1=0.0, x_2=1.0, x_3=1.0, x_4=1.0, x_5=1.0
status: SUCCESS

solution: [2, 3, 4, 5]

../_images/tutorials_09_application_classes_12_1.png

[7]:

# QAOA
meo = MinimumEigenOptimizer(min_eigen_solver=QAOA(reps=1, sampler=Sampler(), optimizer=COBYLA()))
result = meo.solve(qp)
print(result.prettyprint())
print("\nsolution:", prob.interpret(result))
print("\ntime:", result.min_eigen_solver_result.optimizer_time)
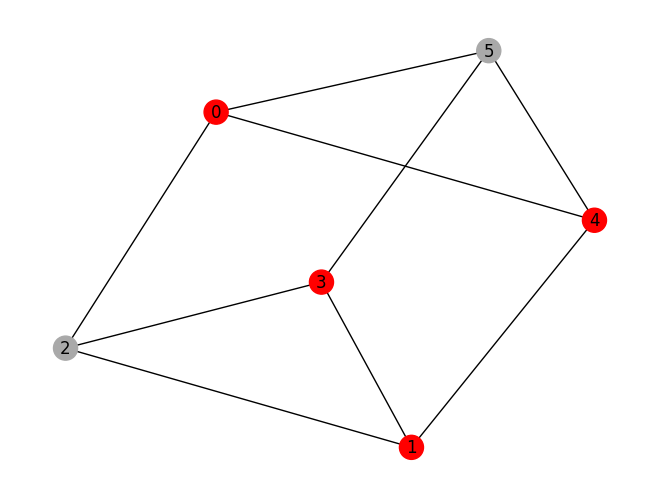
prob.draw(result, pos=pos)

objective function value: 4.0
variable values: x_0=1.0, x_1=1.0, x_2=0.0, x_3=1.0, x_4=1.0, x_5=0.0
status: SUCCESS

solution: [0, 1, 3, 4]

time: 2.721126079559326

../_images/tutorials_09_application_classes_13_1.png

Problema de la mochila (knapsack)#

El problema de la mochila (knapsack) nos pide que encontremos una combinación de artículos de manera que el peso total esté dentro de la capacidad de la mochila y maximicemos el valor total de los artículos. Los siguientes ejemplos resuelven una instancia del problema de la mochila con 5 artículos usando el solucionador propio de Numpy y QAOA.

[8]:

from qiskit_optimization.applications import Knapsack

[9]:

prob = Knapsack(values=[3, 4, 5, 6, 7], weights=[2, 3, 4, 5, 6], max_weight=10)
qp = prob.to_quadratic_program()
print(qp.prettyprint())

Problem name: Knapsack

Maximize
  3*x_0 + 4*x_1 + 5*x_2 + 6*x_3 + 7*x_4

Subject to
  Linear constraints (1)
    2*x_0 + 3*x_1 + 4*x_2 + 5*x_3 + 6*x_4 <= 10  'c0'

  Binary variables (5)
    x_0 x_1 x_2 x_3 x_4

[10]:

# Numpy Eigensolver
meo = MinimumEigenOptimizer(min_eigen_solver=NumPyMinimumEigensolver())
result = meo.solve(qp)
print(result.prettyprint())
print("\nsolution:", prob.interpret(result))

objective function value: 13.0
variable values: x_0=1.0, x_1=1.0, x_2=0.0, x_3=1.0, x_4=0.0
status: SUCCESS

solution: [0, 1, 3]

[11]:

# QAOA
meo = MinimumEigenOptimizer(min_eigen_solver=QAOA(reps=1, sampler=Sampler(), optimizer=COBYLA()))
result = meo.solve(qp)
print(result.prettyprint())
print("\nsolution:", prob.interpret(result))
print("\ntime:", result.min_eigen_solver_result.optimizer_time)

objective function value: 13.0
variable values: x_0=1.0, x_1=1.0, x_2=0.0, x_3=1.0, x_4=0.0
status: SUCCESS

solution: [0, 1, 3]

time: 2.0846190452575684

Cómo revisar el Hamiltoniano#

Si deseas verificar el Hamiltoniano real generado a partir de tu instancia del problema, debes aplicar un convertidor de la siguiente manera.

[12]:

from qiskit_optimization.converters import QuadraticProgramToQubo

[13]:

# the same knapsack problem instance as in the previous section
prob = Knapsack(values=[3, 4, 5, 6, 7], weights=[2, 3, 4, 5, 6], max_weight=10)
qp = prob.to_quadratic_program()
print(qp.prettyprint())

Problem name: Knapsack

Maximize
  3*x_0 + 4*x_1 + 5*x_2 + 6*x_3 + 7*x_4

Subject to
  Linear constraints (1)
    2*x_0 + 3*x_1 + 4*x_2 + 5*x_3 + 6*x_4 <= 10  'c0'

  Binary variables (5)
    x_0 x_1 x_2 x_3 x_4

[14]:

# intermediate QUBO form of the optimization problem
conv = QuadraticProgramToQubo()
qubo = conv.convert(qp)
print(qubo.prettyprint())

Problem name: Knapsack

Minimize
  26*c0@int_slack@0^2 + 104*c0@int_slack@0*c0@int_slack@1
  + 208*c0@int_slack@0*c0@int_slack@2 + 156*c0@int_slack@0*c0@int_slack@3
  + 104*c0@int_slack@1^2 + 416*c0@int_slack@1*c0@int_slack@2
  + 312*c0@int_slack@1*c0@int_slack@3 + 416*c0@int_slack@2^2
  + 624*c0@int_slack@2*c0@int_slack@3 + 234*c0@int_slack@3^2
  + 104*x_0*c0@int_slack@0 + 208*x_0*c0@int_slack@1 + 416*x_0*c0@int_slack@2
  + 312*x_0*c0@int_slack@3 + 104*x_0^2 + 312*x_0*x_1 + 416*x_0*x_2 + 520*x_0*x_3
  + 624*x_0*x_4 + 156*x_1*c0@int_slack@0 + 312*x_1*c0@int_slack@1
  + 624*x_1*c0@int_slack@2 + 468*x_1*c0@int_slack@3 + 234*x_1^2 + 624*x_1*x_2
  + 780*x_1*x_3 + 936*x_1*x_4 + 208*x_2*c0@int_slack@0 + 416*x_2*c0@int_slack@1
  + 832*x_2*c0@int_slack@2 + 624*x_2*c0@int_slack@3 + 416*x_2^2 + 1040*x_2*x_3
  + 1248*x_2*x_4 + 260*x_3*c0@int_slack@0 + 520*x_3*c0@int_slack@1
  + 1040*x_3*c0@int_slack@2 + 780*x_3*c0@int_slack@3 + 650*x_3^2 + 1560*x_3*x_4
  + 312*x_4*c0@int_slack@0 + 624*x_4*c0@int_slack@1 + 1248*x_4*c0@int_slack@2
  + 936*x_4*c0@int_slack@3 + 936*x_4^2 - 520*c0@int_slack@0
  - 1040*c0@int_slack@1 - 2080*c0@int_slack@2 - 1560*c0@int_slack@3 - 1043*x_0
  - 1564*x_1 - 2085*x_2 - 2606*x_3 - 3127*x_4 + 2600

Subject to
  No constraints

  Binary variables (9)
    x_0 x_1 x_2 x_3 x_4 c0@int_slack@0 c0@int_slack@1 c0@int_slack@2
    c0@int_slack@3

[15]:

# qubit Hamiltonian and offset
op, offset = qubo.to_ising()
print(f"num qubits: {op.num_qubits}, offset: {offset}\n")
print(op)

num qubits: 9, offset: 1417.5

SparsePauliOp(['IIIIIIIIZ', 'IIIIIIIZI', 'IIIIIIZII', 'IIIIIZIII', 'IIIIZIIII', 'IIIZIIIII', 'IIZIIIIII', 'IZIIIIIII', 'ZIIIIIIII', 'IIIIIIIZZ', 'IIIIIIZIZ', 'IIIIIIZZI', 'IIIIIZIIZ', 'IIIIIZIZI', 'IIIIIZZII', 'IIIIZIIIZ', 'IIIIZIIZI', 'IIIIZIZII', 'IIIIZZIII', 'IIIZIIIIZ', 'IIIZIIIZI', 'IIIZIIZII', 'IIIZIZIII', 'IIIZZIIII', 'IIZIIIIIZ', 'IIZIIIIZI', 'IIZIIIZII', 'IIZIIZIII', 'IIZIZIIII', 'IIZZIIIII', 'IZIIIIIIZ', 'IZIIIIIZI', 'IZIIIIZII', 'IZIIIZIII', 'IZIIZIIII', 'IZIZIIIII', 'IZZIIIIII', 'ZIIIIIIIZ', 'ZIIIIIIZI', 'ZIIIIIZII', 'ZIIIIZIII', 'ZIIIZIIII', 'ZIIZIIIII', 'ZIZIIIIII', 'ZZIIIIIII'],
              coeffs=[-258.5+0.j, -388. +0.j, -517.5+0.j, -647. +0.j, -776.5+0.j, -130. +0.j,
 -260. +0.j, -520. +0.j, -390. +0.j,   78. +0.j,  104. +0.j,  156. +0.j,
  130. +0.j,  195. +0.j,  260. +0.j,  156. +0.j,  234. +0.j,  312. +0.j,
  390. +0.j,   26. +0.j,   39. +0.j,   52. +0.j,   65. +0.j,   78. +0.j,
   52. +0.j,   78. +0.j,  104. +0.j,  130. +0.j,  156. +0.j,   26. +0.j,
  104. +0.j,  156. +0.j,  208. +0.j,  260. +0.j,  312. +0.j,   52. +0.j,
  104. +0.j,   78. +0.j,  117. +0.j,  156. +0.j,  195. +0.j,  234. +0.j,
   39. +0.j,   78. +0.j,  156. +0.j])

[16]:

import qiskit.tools.jupyter

%qiskit_version_table
%qiskit_copyright

Version Information

Qiskit Software	Version
`qiskit-terra`	0.25.0.dev0+1d844ec
`qiskit-aer`	0.12.0
`qiskit-ibmq-provider`	0.20.2
`qiskit-nature`	0.7.0
`qiskit-optimization`	0.6.0
System information
Python version	3.10.11
Python compiler	Clang 14.0.0 (clang-1400.0.29.202)
Python build	main, Apr 7 2023 07:31:31
OS	Darwin
CPUs	4
Memory (Gb)	16.0
Thu May 18 16:57:10 2023 JST

This code is a part of Qiskit

This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.

Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.

[ ]: