Nota
Esta página fue generada a partir de docs/tutorials/07_examples_vehicle_routing.ipynb.
Rutas de Vehículos#
Introducción#
La logística es una industria importante, y algunas estimaciones la valoran en USD 8.183 billones a nivel mundial en 2015. La mayoría de los proveedores de servicios operan varios vehículos (por ejemplo, camiones y portacontenedores), varios depósitos, donde los vehículos pasan la noche y sirven una serie de ubicaciones de clientes con cada vehículo durante cada día. Hay muchos problemas de optimización y control que consideran estos parámetros. Computacionalmente, el desafío clave es cómo diseñar rutas desde los depósitos a una serie de ubicaciones de clientes y de regreso al depósito, a fin de minimizar las millas recorridas por los vehículos, el tiempo empleado o funciones objetivo similares. En este cuaderno formalizamos una versión idealizada del problema y mostramos su solución utilizando el enfoque de optimización aproximada cuántica de Farhi, Goldstone, y Gutmann (2014).
El flujo de trabajo en general que demostramos comprende:
establecer las ubicaciones de los clientes. Normalmente, estos estarían disponibles antes del día de las entregas desde una base de datos. En nuestro caso de uso, los generamos aleatoriamente.
calcular las distancias por pares, tiempos de viaje o similares. En nuestro caso, consideramos la distancia euclidiana, «a vuelo de pájaro», que es quizás la más simple posible.
calcular las rutas en sí. Este paso se ejecuta dos veces, de hecho. Primero, obtenemos un valor de referencia por una ejecución de un solucionador clásico (IBM CPLEX) en la computadora clásica. Segundo, ejecutamos un algoritmo híbrido alternativo parcialmente en la computadora cuántica.
visualización de los resultados. En nuestro caso esto, de nuevo, es una simple gráfica.
A continuación, explicamos primero el modelo, antes de proceder con la instalación de los requerimientos previos y la carga de datos.
El Modelo#
Matemáticamente hablando, el problema de enrutamiento de vehículos (vehicle routing problem, VRP) es un problema combinatorio, en el que se buscan las mejores rutas desde un depósito a varios clientes y de regreso al depósito, dado un número de vehículos disponibles. Hay varias formulaciones posibles, que extienden una serie de formulaciones del problema del vendedor viajero [Applegate et al, 2006]. Aquí, presentamos una formulación conocida como MTZ [Miller, Tucker, Zemlin, 1960].
Sea \(n\) el número de clientes (indexado como \(1,\dots,n\)) y \(K\) el número de vehículos disponibles. Sea \(x_{ij} = \{0,1\}\) la variable de decisión binaria que, si es \(1\), activa el segmento desde el nodo \(i\) al nodo \(j\). El índice de nodo va desde \(0\) a \(n\), donde \(0\) es (por convención) el depósito. Hay el doble de variables de decisión distintas que de aristas. Por ejemplo, en un grafo completamente conectado, hay \(n(n+1)\) variables de decisión binarias.
Si dos nodos \(i\) y \(j\) tienen un enlace desde \(i\) a \(j\), escribimos \(i \sim j\). También denotamos con \(\delta(i)^+\) el conjunto de nodos a los que \(i\) tiene un enlace, es decir, \(j \in \delta(i)^+\) si y solo si \(i \sim j\). De manera similar, denotamos con \(\delta(i)^-\) el conjunto de nodos que están conectados a \(i\), en el sentido de que \(j \in \delta(i)^-\) si y solo si \(j \sim i\).
Además, consideramos variables continuas, para todos los nodos \(i = 1,\dots, n\), denotadas \(u_i\). Estas variables son necesarias en la formulación MTZ del problema para eliminar sub-recorridos entre clientes.
El VRP puede formularse como:
sujeto a la restricción de visita de nodos:
las restricciones de las visitas al depósito:
y las restricciones de eliminación del sub-recorrido:
En particular,
La función de costo es lineal en las funciones de costo y pondera los diferentes arcos basados en un peso positivo \(w_{ij}>0\) (típicamente la distancia entre el nodo \(i\) y el nodo \(j\));
El primer conjunto de restricciones impone que desde y hacia cada cliente, solo se permite un enlace;
El segundo conjunto de restricciones impone que desde y hacia el depósito, se permiten exactamente \(K\) enlaces;
El tercer conjunto de restricciones impone las restricciones de eliminación del sub-recorrido y son cotas en \(u_i\), con \(Q>q_j>0\), y \(Q,q_i \in \mathbb{R}\).
Solución clásica#
Podemos resolver el VRP de forma clásica, por ejemplo, utilizando CPLEX. CPLEX usa un método de bifurcación, unión y corte para encontrar una solución aproximada del VRP, que, en esta formulación, es un programa lineal de enteros mixtos (MILP). En aras de la notación, empaquetamos las variables de decisión en un vector como
donde \({\bf z} \in \{0,1\}^N\), con \(N = n (n+1)\). Entonces, la dimensión del problema se escala cuadráticamente con el número de nodos. Denotemos la solución óptima con \({\bf z}^*\), y el costo óptimo asociado \(f^*\).
Solución cuántica#
Aquí, demostramos un enfoque que combina los pasos de la computación clásica y cuántica, siguiendo el enfoque de optimización cuántica aproximada de Farhi, Goldstone y Gutmann (2014). En particular, utilizamos el solucionador propio cuántico variacional (variational quantum eigensolver, VQE). Destacamos que dado el uso de profundidad limitada de los circuitos cuánticos empleados (formas variacionales), es difícil discutir la aceleración del algoritmo, ya que la solución obtenida es de naturaleza heurística. Al mismo tiempo, debido a la naturaleza e importancia de los problemas de destino, vale la pena investigar enfoques heurísticos, que pueden ser útiles para algunas clases de problemas.
El algoritmo puede resumirse de la siguiente manera:
Pasos de preparación:
Transformar el problema combinatorio en un problema de optimización de polinomios binarios con restricciones de igualdad solamente;
Mapear el problema resultante en un Hamiltoniano Ising (\(H\)) para las variables \({\bf z}\) y la base \(Z\), mediante métodos de penalización si es necesario;
Elegir la profundidad del circuito cuántico \(m\). Se debe tener en cuenta que la profundidad se puede modificar de forma adaptativa.
Elegir un conjunto de controles \(\theta\) y crear una función de prueba \(\big|\psi(\boldsymbol\theta)\rangle\), construida usando un circuito cuántico hecho de compuertas C-Phase y rotaciones Y de un solo qubit, parametrizada por los componentes de \(\boldsymbol\theta\).
Pasos del algoritmo:
Evaluar \(C(\boldsymbol\theta) = \langle\psi(\boldsymbol\theta)\big|H\big|\psi(\boldsymbol\theta)\rangle\) muestreando el resultado del circuito en la base Z y sumando los valores esperados de los términos Ising individuales. En general, se deben estimar diferentes puntos de control alrededor de \(\boldsymbol\theta\), dependiendo del optimizador clásico elegido.
Utilizar un optimizador clásico para elegir un nuevo conjunto de controles.
Continuar hasta que \(C(\boldsymbol\theta)\) alcance un mínimo, lo suficientemente cercano a la solución \(\boldsymbol\theta^*\).
Utilizar la última \(\boldsymbol\theta\) para generar un conjunto final de muestras de la distribución \(\Big|\langle z_i\big|\psi(\boldsymbol\theta)\rangle\Big|^2\;\forall i\) para obtener la respuesta.
Hay muchos parámetros en todo momento, en particular la elección de la función de onda de prueba. A continuación, consideramos:
donde \(U_\mathrm{entrelazador}\) es una colección de compuertas C-Phase (compuertas totalmente entrelazadas), y \(U_\mathrm{simple}(\theta) = \prod_{i=1}^N Y(\theta_{i})\), donde \(N\) es el número de qubits y \(m\) es la profundidad del circuito cuántico.
Construir el Hamiltoniano de Ising#
Del \(VRP\) se puede construir una optimización polinomial binaria con restricciones de igualdad solo considerando los casos en los que \(K=n-1\). En estos casos, las restricciones de eliminación del sub-recorrido no son necesarias y el problema está solamente en la variable \({\bf z}\). En particular, podemos escribir un Lagrangiano aumentado como
donde \(A\) es un parámetro suficientemente grande.
Del Hamiltoniano a la formulación QP#
En el vector \({\bf z}\), y para un grafo completo (\(\delta(i)^+ = \delta(i)^- = \{0,1,\dots,i-1,i+1,\dots,n\}\)), \(H\) se puede escribir de la siguiente manera.
Esto es:
Donde: el primer término:
El segundo término:
El tercer término:
La formulación QP del Hamiltoniano de Ising está lista para el uso de VQE. Resolveremos el QP usando la pila de optimización disponible en Qiskit Optimization.
Referencias#
[1] E. Farhi, J. Goldstone, S. Gutmann e-print arXiv 1411.4028, 2014
[2] Max-Cut y Problema del Vendedor Viajero
[3] C. E. Miller, E. W. Tucker, and R. A. Zemlin (1960). «Integer Programming Formulations and Travelling Salesman Problems». J. ACM. 7: 326–329. doi:10.1145/321043.321046.
[4] D. L. Applegate, R. M. Bixby, V. Chvátal, and W. J. Cook (2006). The Traveling Salesman Problem. Princeton University Press, ISBN 978-0-691-12993-8.
Inicialización#
En primer lugar, cargamos todos los paquetes que necesitamos. Se requiere CPLEX para los cálculos clásicos. Puedes instalarlo mediante pip install 'qiskit-optimization[cplex]'.
[1]:
import numpy as np
import matplotlib.pyplot as plt
try:
import cplex
from cplex.exceptions import CplexError
except:
print("Warning: Cplex not found.")
import math
from qiskit_algorithms.utils import algorithm_globals
from qiskit_algorithms import SamplingVQE
from qiskit_algorithms.optimizers import SPSA
from qiskit.circuit.library import RealAmplitudes
from qiskit.primitives import Sampler
Luego inicializamos las variables
[2]:
# Initialize the problem by defining the parameters
n = 3 # number of nodes + depot (n+1)
K = 2 # number of vehicles
Definimos una clase de inicialización que coloca aleatoriamente los nodos en un plano 2-D y calcula la distancia entre ellos.
[3]:
# Get the data
class Initializer:
def __init__(self, n):
self.n = n
def generate_instance(self):
n = self.n
# np.random.seed(33)
np.random.seed(1543)
xc = (np.random.rand(n) - 0.5) * 10
yc = (np.random.rand(n) - 0.5) * 10
instance = np.zeros([n, n])
for ii in range(0, n):
for jj in range(ii + 1, n):
instance[ii, jj] = (xc[ii] - xc[jj]) ** 2 + (yc[ii] - yc[jj]) ** 2
instance[jj, ii] = instance[ii, jj]
return xc, yc, instance
[4]:
# Initialize the problem by randomly generating the instance
initializer = Initializer(n)
xc, yc, instance = initializer.generate_instance()
Solución clásica utilizando IBM ILOG CPLEX#
Para una solución clásica, utilizamos IBM ILOG CPLEX. CPLEX puede encontrar la solución exacta de este problema. Primero definimos una clase ClassicalOptimizer que codifica el problema de una manera que CPLEX pueda resolver, y luego instanciamos la clase y la resolvemos.
[5]:
class ClassicalOptimizer:
def __init__(self, instance, n, K):
self.instance = instance
self.n = n # number of nodes
self.K = K # number of vehicles
def compute_allowed_combinations(self):
f = math.factorial
return f(self.n) / f(self.K) / f(self.n - self.K)
def cplex_solution(self):
# refactoring
instance = self.instance
n = self.n
K = self.K
my_obj = list(instance.reshape(1, n**2)[0]) + [0.0 for x in range(0, n - 1)]
my_ub = [1 for x in range(0, n**2 + n - 1)]
my_lb = [0 for x in range(0, n**2)] + [0.1 for x in range(0, n - 1)]
my_ctype = "".join(["I" for x in range(0, n**2)]) + "".join(
["C" for x in range(0, n - 1)]
)
my_rhs = (
2 * ([K] + [1 for x in range(0, n - 1)])
+ [1 - 0.1 for x in range(0, (n - 1) ** 2 - (n - 1))]
+ [0 for x in range(0, n)]
)
my_sense = (
"".join(["E" for x in range(0, 2 * n)])
+ "".join(["L" for x in range(0, (n - 1) ** 2 - (n - 1))])
+ "".join(["E" for x in range(0, n)])
)
try:
my_prob = cplex.Cplex()
self.populatebyrow(my_prob, my_obj, my_ub, my_lb, my_ctype, my_sense, my_rhs)
my_prob.solve()
except CplexError as exc:
print(exc)
return
x = my_prob.solution.get_values()
x = np.array(x)
cost = my_prob.solution.get_objective_value()
return x, cost
def populatebyrow(self, prob, my_obj, my_ub, my_lb, my_ctype, my_sense, my_rhs):
n = self.n
prob.objective.set_sense(prob.objective.sense.minimize)
prob.variables.add(obj=my_obj, lb=my_lb, ub=my_ub, types=my_ctype)
prob.set_log_stream(None)
prob.set_error_stream(None)
prob.set_warning_stream(None)
prob.set_results_stream(None)
rows = []
for ii in range(0, n):
col = [x for x in range(0 + n * ii, n + n * ii)]
coef = [1 for x in range(0, n)]
rows.append([col, coef])
for ii in range(0, n):
col = [x for x in range(0 + ii, n**2, n)]
coef = [1 for x in range(0, n)]
rows.append([col, coef])
# Sub-tour elimination constraints:
for ii in range(0, n):
for jj in range(0, n):
if (ii != jj) and (ii * jj > 0):
col = [ii + (jj * n), n**2 + ii - 1, n**2 + jj - 1]
coef = [1, 1, -1]
rows.append([col, coef])
for ii in range(0, n):
col = [(ii) * (n + 1)]
coef = [1]
rows.append([col, coef])
prob.linear_constraints.add(lin_expr=rows, senses=my_sense, rhs=my_rhs)
[6]:
# Instantiate the classical optimizer class
classical_optimizer = ClassicalOptimizer(instance, n, K)
# Print number of feasible solutions
print("Number of feasible solutions = " + str(classical_optimizer.compute_allowed_combinations()))
Number of feasible solutions = 3.0
[7]:
# Solve the problem in a classical fashion via CPLEX
x = None
z = None
try:
x, classical_cost = classical_optimizer.cplex_solution()
# Put the solution in the z variable
z = [x[ii] for ii in range(n**2) if ii // n != ii % n]
# Print the solution
print(z)
except:
print("CPLEX may be missing.")
[1.0, 1.0, 1.0, 0.0, 1.0, 0.0]
[8]:
# Visualize the solution
def visualize_solution(xc, yc, x, C, n, K, title_str):
plt.figure()
plt.scatter(xc, yc, s=200)
for i in range(len(xc)):
plt.annotate(i, (xc[i] + 0.15, yc[i]), size=16, color="r")
plt.plot(xc[0], yc[0], "r*", ms=20)
plt.grid()
for ii in range(0, n**2):
if x[ii] > 0:
ix = ii // n
iy = ii % n
plt.arrow(
xc[ix],
yc[ix],
xc[iy] - xc[ix],
yc[iy] - yc[ix],
length_includes_head=True,
head_width=0.25,
)
plt.title(title_str + " cost = " + str(int(C * 100) / 100.0))
plt.show()
if x is not None:
visualize_solution(xc, yc, x, classical_cost, n, K, "Classical")
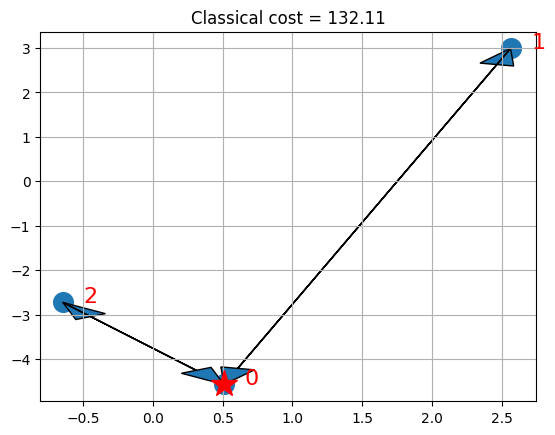
Si tienes CPLEX, la solución muestra el depósito con una estrella y las rutas seleccionadas para los vehículos con flechas.
Solución cuántica desde cero#
Para la solución cuántica, utilizamos Qiskit.
Primero, derivamos la solución desde cero, usando una clase QuantumOptimizer que codifica el enfoque cuántico para resolver el problema y luego lo instanciamos y lo resolvemos. Definimos los siguientes métodos dentro de la clase:
binary_representation: codifica el problema \((M)\) en términos QP (que es básicamente álgebra lineal);construct_problem: construye un problema de optimización QUBO como una instancia deQuadraticProgram;solve_problem: resuelve el problema \((M)\) construido en el paso anterior a través delMinimunEigenOptimizerusandoSamplingVQEcon parámetros predeterminados;
[9]:
from qiskit_optimization import QuadraticProgram
from qiskit_optimization.algorithms import MinimumEigenOptimizer
class QuantumOptimizer:
def __init__(self, instance, n, K):
self.instance = instance
self.n = n
self.K = K
def binary_representation(self, x_sol=0):
instance = self.instance
n = self.n
K = self.K
A = np.max(instance) * 100 # A parameter of cost function
# Determine the weights w
instance_vec = instance.reshape(n**2)
w_list = [instance_vec[x] for x in range(n**2) if instance_vec[x] > 0]
w = np.zeros(n * (n - 1))
for ii in range(len(w_list)):
w[ii] = w_list[ii]
# Some variables I will use
Id_n = np.eye(n)
Im_n_1 = np.ones([n - 1, n - 1])
Iv_n_1 = np.ones(n)
Iv_n_1[0] = 0
Iv_n = np.ones(n - 1)
neg_Iv_n_1 = np.ones(n) - Iv_n_1
v = np.zeros([n, n * (n - 1)])
for ii in range(n):
count = ii - 1
for jj in range(n * (n - 1)):
if jj // (n - 1) == ii:
count = ii
if jj // (n - 1) != ii and jj % (n - 1) == count:
v[ii][jj] = 1.0
vn = np.sum(v[1:], axis=0)
# Q defines the interactions between variables
Q = A * (np.kron(Id_n, Im_n_1) + np.dot(v.T, v))
# g defines the contribution from the individual variables
g = (
w
- 2 * A * (np.kron(Iv_n_1, Iv_n) + vn.T)
- 2 * A * K * (np.kron(neg_Iv_n_1, Iv_n) + v[0].T)
)
# c is the constant offset
c = 2 * A * (n - 1) + 2 * A * (K**2)
try:
max(x_sol)
# Evaluates the cost distance from a binary representation of a path
fun = (
lambda x: np.dot(np.around(x), np.dot(Q, np.around(x)))
+ np.dot(g, np.around(x))
+ c
)
cost = fun(x_sol)
except:
cost = 0
return Q, g, c, cost
def construct_problem(self, Q, g, c) -> QuadraticProgram:
qp = QuadraticProgram()
for i in range(n * (n - 1)):
qp.binary_var(str(i))
qp.objective.quadratic = Q
qp.objective.linear = g
qp.objective.constant = c
return qp
def solve_problem(self, qp):
algorithm_globals.random_seed = 10598
vqe = SamplingVQE(sampler=Sampler(), optimizer=SPSA(), ansatz=RealAmplitudes())
optimizer = MinimumEigenOptimizer(min_eigen_solver=vqe)
result = optimizer.solve(qp)
# compute cost of the obtained result
_, _, _, level = self.binary_representation(x_sol=result.x)
return result.x, level
Paso 1#
Crear una instancia de la clase del optimizador cuántico con parámetros:
la instancia;
el número de nodos y vehículos
nyK;
[10]:
# Instantiate the quantum optimizer class with parameters:
quantum_optimizer = QuantumOptimizer(instance, n, K)
Paso 2#
Codificar el problema como una formulación binaria (IH-QP).
Comprobación: asegurarse que la formulación binaria del optimizador cuántico es correcta (es decir, que da el mismo costo dada la misma solución).
[11]:
# Check if the binary representation is correct
try:
if z is not None:
Q, g, c, binary_cost = quantum_optimizer.binary_representation(x_sol=z)
print("Binary cost:", binary_cost, "classical cost:", classical_cost)
if np.abs(binary_cost - classical_cost) < 0.01:
print("Binary formulation is correct")
else:
print("Error in the binary formulation")
else:
print("Could not verify the correctness, due to CPLEX solution being unavailable.")
Q, g, c, binary_cost = quantum_optimizer.binary_representation()
print("Binary cost:", binary_cost)
except NameError as e:
print("Warning: Please run the cells above first.")
print(e)
Binary cost: 132.11148115684045 classical cost: 132.1114811568365
Binary formulation is correct
Paso 3#
Codificar el problema como una instancia de QuadraticProgram.
[12]:
qp = quantum_optimizer.construct_problem(Q, g, c)
Paso 4#
Resolver el problema a través de MinimumEigenOptimizer de la pila de optimización. Nótese bien que dependiendo del número de qubits, la simulación de vector de estado puede tardar un poco; por ejemplo, con 12 qubits, se necesitan más de 12 horas. El registro (log) es útil para ver qué está haciendo el programa.
[13]:
quantum_solution, quantum_cost = quantum_optimizer.solve_problem(qp)
print(quantum_solution, quantum_cost)
[1. 1. 1. 0. 1. 0.] 132.11148115684045
Paso 5#
Visualizar la solución
[14]:
# Put the solution in a way that is compatible with the classical variables
x_quantum = np.zeros(n**2)
kk = 0
for ii in range(n**2):
if ii // n != ii % n:
x_quantum[ii] = quantum_solution[kk]
kk += 1
# visualize the solution
visualize_solution(xc, yc, x_quantum, quantum_cost, n, K, "Quantum")
# and visualize the classical for comparison
if x is not None:
visualize_solution(xc, yc, x, classical_cost, n, K, "Classical")
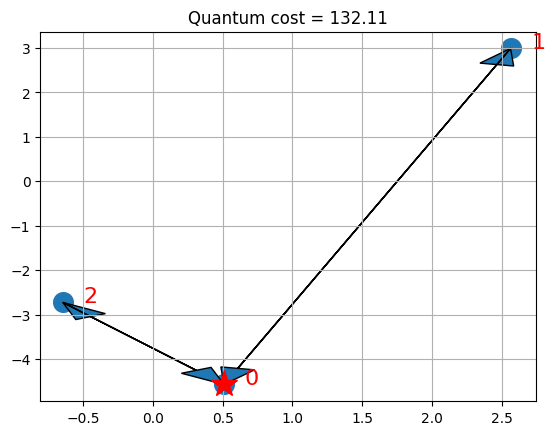
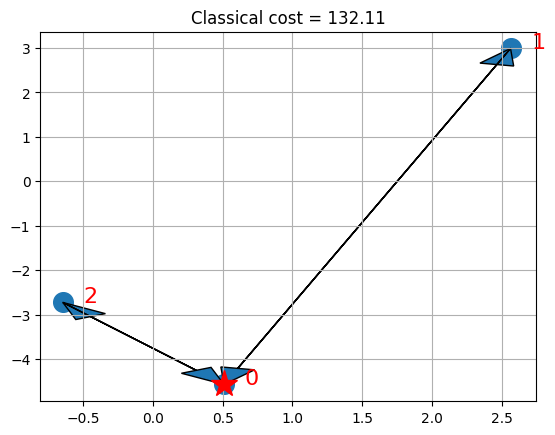
Las gráficas presentan el depósito con una estrella y las rutas seleccionadas para los vehículos con flechas. Ten en cuenta que en este caso particular, podemos encontrar la solución óptima de la formulación QP, que coincide con la solución óptima del ILP.
Ten en cuenta que VQE es una heurística que trabaja en la formulación QP del Hamiltoniano de Ising. Para elecciones adecuadas de A, los óptimos locales de la formulación de QP serán soluciones factibles para el ILP. Mientras que para algunos casos pequeños, como el anterior, podemos encontrar soluciones óptimas de la formulación QP que coincidan con los óptimos del ILP, encontrar soluciones óptimas del ILP es más difícil que encontrar los óptimos locales de la formulación QP, en general, que a su vez es más difícil que encontrar soluciones viables del ILP. Incluso dentro del VQE, se pueden proporcionar garantías más sólidas, para formas variacionales específicas (funciones de onda de prueba).
[15]:
import qiskit.tools.jupyter
%qiskit_version_table
%qiskit_copyright
Version Information
| Qiskit Software | Version |
|---|---|
qiskit-terra | 0.23.0 |
qiskit-aer | 0.11.1 |
qiskit-optimization | 0.5.0 |
qiskit-machine-learning | 0.6.0 |
| System information | |
| Python version | 3.9.15 |
| Python compiler | Clang 14.0.0 (clang-1400.0.29.102) |
| Python build | main, Oct 11 2022 22:27:25 |
| OS | Darwin |
| CPUs | 4 |
| Memory (Gb) | 16.0 |
| Tue Dec 06 21:53:30 2022 JST | |
This code is a part of Qiskit
© Copyright IBM 2017, 2022.
This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.
[ ]: