নোট
এই পৃষ্ঠাটি docs/tutorials/07_examples_vehicle_routing.ipynb থেকে বানানো হয়েছে।
বাহন(ভেহিকেল) রাউটিং#
ভূমিকা#
সরবরাহ শিল্প একটি বড় শিল্প,২০১৫ সালে যার অনুমাকি বাজার মূল্য ছিল ৮১৮৩ মার্কিন ডলার।প্রায় সমস্ত সেবা প্রদানকারী অনেক গুলি বাহন(যেমন মাল বোঝাই গাড়ি ও জাহাজ),অনেক গুলি ডিপো ব্যাবহার করেন যেখানে বাহন গুলি এক রাতের জন্যে এবং অনেকগুলি খরিদ্দারকে বিভিন্ন জায়গায় সামগ্রী সরবরাহ করে থাকে প্রতিটি বাহন দ্বারা প্রতিদিন। এই স্থিতিমাপ গুলিকে অনেক অপটিমাইজেশন এবং নিয়ন্ত্রণ সমস্যা(কন্ট্রোল প্রবলেম) দ্বারা গণ্য করা হয়। গাণিতিক ভাবে মূল সমস্যা হলো এই রুট বা যাত্রাপথ গুলিকে এমন ভাবে নকশা বা ডিজাইন করা যাতে কম যাত্রা পথ অতিক্রান্ত করে ,কম সময়ে বা অনুরূপ নৈর্ব্যক্তিক অন্বয় (অব্জেক্টিভ ফাংশন) কাজটি করা যায়।এই নোটবুকের মধ্যে আমরা এই সমস্যার একটি আদর্শ সংস্করণ বিধিবদ্ধ করব এবং তার সমাধান দেখাব ফারহি ,গোল্ডস্টেইন এবং গুটম্যানের (২০১৪) কোয়ান্টাম আনুমানিক অপটিমাইজেশন প্রন্থা দ্বারা।
সামগ্রিকভাবে আমাদের প্রদর্শিত কর্মধারা গঠিত হয়:
খরিদ্দারের স্থান প্রতিষ্টিত করা। সাধারণত,এগুলি পাওয়া যাবে একটি ডাটাবেজ (দস্তাবেজ) থেকে বিতরণের দিনের আগে।আমাদের ব্যবহারিক ক্ষেত্র আমরা এটি সৃষ্টি করি এলোমেলো ভাবে বা যদৃচ্ছভাবে।
compute the pair-wise distances, travel times, or similar. In our case, we consider the Euclidean distance, "as the crow flies", which is perhaps the simplest possible.
আসল রুট গুলি গননা করো।আসলে এই ধাপটি দুবার চালানো হয়।প্রথমে আমরা একটি তথ্যসূত্র (রেফারেন্স) মান প্রাপ্ত করি একটি প্রথাগত (ক্লাসিক্যাল) সমাধানকারী (সলভার)(IBM CPLEX) একটি প্রথাগত প্রথাগত (ক্লাসিক্যাল) কম্পিউটারে চালিয়ে।দ্বিতীয়তে আংশিক ভাবে একটি কোয়ান্টাম কম্পিউটারে আমরা একটি বিকল্প, হাইব্রিড অ্যালগরিদম / ধরাক্রম চালায়।
ফলাফল দৃশ্যায়ন বা চিত্রায়ন।আমাদের ক্ষেত্রে,এটি আবার একটি সহজ সরললে খচিত্র বা আঁকা(প্লট)।
এটিতে আমরা প্রথমে নকশাটিকে বর্ণনা করবো, পূর্ব প্রয়োজনীয় (প্রী রিকুইসিট) অধিষ্ঠানকরণ(ইনস্টলেশন) এবং তথ্য বোঝাই বা লোডিং করার আগে।
নকশা#
গাণিতিক ভাবে বললে,ভেহিকেল বা বাহন রাউটিং সমস্যা (ভি.পি.আর.)হলো একটি সমাবেশ সমস্যা,দিয়ে রাখা কিছু সংখ্যক বাহনের জন্যে সবচেয়ে ভালো রাস্তা বা রুট জানতে চাওয়া হয় ডিপো বা গুদামঘর থেকে খরিদ্দার পর্যন্ত।এখানে অনেক গুলি সূত্র সম্ভব,ট্র্যাভেলিইং সেলসম্যান সমস্যার[Applegate et al, 2006] বেশ কয়েকটি সূত্র প্রসারিত করে।আমরা এখানে একটি সূত্র পেশ করছি যাকে বলা হয় এম.টি.জেড [Miller, Tucker, Zemlin, 1960]।
ধরা জাক \(n\) খরিদ্দারের সংখ্যা(সূচিত হয় \(1,\dots,n\) দ্বারা),এবং \(K\) হলো বাহন বা গাড়ির সংখ্যা। ধরা জাক \(x_{ij} = \{0,1\}\) হলোদ্বিমিক (বাইনারি) সিদ্ধান্ত বা ডিসিসন চল রাশি যেটি যদি \(1\) থাকে তবে সেটি বিভাগটিকে সক্রিয় করে \(i\) নোড থেকে \(j\) নোডে। নোড সূচক চলে \(0\) থেকে \(n\) পর্যন্ত,যেখানে \(0\) হলো ডিপোটি বা গুদামঘরটি (প্রচলিত ভাবে)।প্রান্ত হিসাবে দ্বিগুণ স্বতন্ত্র সিদ্ধান্তের চলরশি রয়েছে। উদাহরণ স্বরূপ একটি পূর্ণ সংযুক্ত গ্রাফে \(n(n+1)\) গুলি দ্বিমিক (বাইনারি) সিদ্ধান্ত চলরাশি রয়েছে।
যদি দুটি নোড \(i\) এবং math:j মধ্যে যোগ থাকে \(i\) থেকে \(j\) তে,তখন আমরা লিখবো \(i \sim j\)। এছাড়াও আমরা সেই নোডের সেট টিকে চিহ্নিত করি \(\delta(i)^+\) দ্বারা যার সাথে \(i\) একটি যোগাযোগ আছে,যেমন \(j \in \delta(i)^+\) শুধুমাত্র তখন যখন \(i \sim j\) । একইরকম ভাবে সেই নোডের সেটকে করি \(\delta(i)^-\) দ্বারা যেগুলি \(i\) sathe সংযুক্ত,এই ভাবে যে \(j \in \delta(i)^-\) শুধুমাত্র তখন যখন \(j \sim i\)।
উপরন্তু,আমরা বিবেচনা করবো ক্রমাগত চল রাশি ,সমস্ত \(i = 1,\dots, n\) জন্যে , চিহ্নিত হয় \(u_i\)। এই চল রাশি গুলি প্রয়োজন সমস্যার এম.টি.জেড. সূত্রে খরিদ্দারের মধ্যে উপ - ভ্রমণ পরিহার করার জন্যে।
ভি.পি.আর. টিকে সুত্রাইত করা যাবে এই ভাবে:
নোড-পরিদর্শন সীমাবদ্ধতা সাপেক্ষে:
ডিপো বা গুদামঘর সীমাবদ্ধতা:
এবং উপ - ভ্রমণ পরিহার করার সীমাবদ্ধতা:
In particular,
The cost function is linear in the cost functions and weighs the different arches based on a positive weight \(w_{ij}>0\) (typically the distance between node \(i\) and node \(j\));
The first set of constraints enforce that from and to every client, only one link is allowed;
The second set of constraints enforce that from and to the depot, exactly \(K\) links are allowed;
The third set of constraints enforce the sub-tour elimination constraints and are bounds on \(u_i\), with \(Q>q_j>0\), and \(Q,q_i \in \mathbb{R}\).
প্রথাগত (ক্লাসিক্যাল) সমাধান#
আমরা সি.পি.এল.এক্স ব্যবহার করে ক্লাসিকালি বা প্রথাগত ভি.আর.পি সমাধান করতে পারি। ভি.আর.পি-র একটি আনুমানিক সমাধান খুঁজে পেতে সি.পি.এল.এক্স একটি শাখা-এবং-সীমাবদ্ধ এবং কাটা( ব্রাঞ্চ অ্যান্ড বউন্ড অ্যান্ড কাট) পদ্ধতি ব্যবহার করে, যা এই সূচনায়, একটি মিশ্র-পূর্ণসংখ্যার লিনিয়ার প্রোগ্রাম (এম.আই.এল.পি)।স্বরলিপিটির খাতিরে, আমরা সিদ্ধান্ত চল রশিগুলিকে গুচ্ছ করি একটিি ভেক্টরে যেমন
যার মধ্যে: \({\bf z} \in \{0,1\}^N\), সাথে \(N = n (n+1)\)।সুতরাং সমস্যাটির মাত্রা নোডের সংখ্যার সাথে চতুর্ভুজ ভাবে স্কেল করে।আসুন আমরা সর্বোত্তম সমাধানটি \({\bf z}^*\) এর দ্বারা চিহ্নিত করি, এবং সম্পর্কিত সর্বাপেক্ষা কাম্য ব্যয় \(f^*\)।
কোয়ান্টাম সমাধান#
এখানে, আমরা একটি পদ্ধতির প্রদর্শন করি যা ক্লাসিক্যাল এবং কোয়ান্টাম কম্পিউটিং পদক্ষেপের সংমিশ্রণ করে, ফারহী, গোল্ডস্টোন এবং গুটম্যান (২০১৪) এর কোয়ান্টাম আনুমানিক অপ্টিমাইজেশন পদ্ধতির অনুসরণ করে।বিশেষত, আমরা ভেরিয়েশনাল কোয়ান্টাম আইজেনসলভার (ভিকিউই) ব্যবহার করি।আমরা জোর দিয়েছি যে নিযুক্ত কোয়ান্টাম বর্তনী বা সার্কিটগুলির (ভেরিয়েশনাল ফর্ম)সীমিত গভীরতার ব্যবহারের কারণে,অ্যালগরিদমের গতি বাড়ানো নিয়ে আলোচনা করা শক্ত, কারণ প্রাপ্ত সমাধানটি প্রকৃতিতে হিউরিস্টিক বা তাত্ত্বিক । একই সময়ে, লক্ষ্য বা টার্গেট সমস্যার প্রকৃতি এবং গুরুত্বের কারণে, বৈজ্ঞানিক বা তাত্ত্বিক পদ্ধতির তদন্ত মূল্যবান, যা কিছু সমস্যা শ্রেণীর জন্য উপযুক্ত হতে পারে।
The algorithm can be summarized as follows:
প্রস্তুতির ধাপ:
সমাবেশ সমস্যাটিকে একটা সমতা শর্তসাপেক্ষ দ্বিমিক (বাইনারি) বহুরাশিক অনুকূলায়ন (অপ্টিমাইজেশন) সমস্যায় রূপান্তর;
\({\bf z}\) এবং বেসিস(ভিত্তি) \(Z\) চলরাশির জন্য প্রাপ্ত সমস্যা একটা আইসিং হ্যামিল্টোনিয়ান (\(H\)) -এ চিত্রায়িত করা, প্রয়োজনে শাস্তিমূলক (পেনাল্টি) পদ্ধতি ব্যবহার করে।
কোয়ান্টাম সার্কিট :math:`m -র গভীরতা চয়ন করুন: । টীকা: গভীরতাটি অভিযোজিতভাবে সংশোধন করা যেতে পারে।
একটা নিয়ন্ত্রণকারীর সেট \(\theta\) নির্বাচিত করে একটা পরীক্ষা ফাংশন \(\big|\psi(\boldsymbol\theta)\rangle\) বানানো হলো, যেটা একটা কোয়ান্টাম বর্তনী (সার্কিট) যেটা আবার C-Phase গেট এবং একক কিউবিট Y ঘূর্ণন যাতে প্যারামিটাররূপে \(\boldsymbol\theta\) -এর বিভিন্ন অংশ আছে।
অ্যালগরিদম / ধরাক্রম পদক্ষেপ:
মূল্যায়ন কর \(C(\boldsymbol\theta) = \langle\psi(\boldsymbol\theta)\big|H\big|\psi(\boldsymbol\theta)\rangle\) জেড(Z) বেসিস বা ভিত্তিতে বর্তনীর (সার্কিট) ফলাফল গুলি নমুনা (স্যাম্পল) করে এবং একসাথে পৃথক আইসিং পদগুলির প্রত্যাশিত মান যুক্ত করে। সাধারণভাবে,:math:boldsymboltheta চারপাশে বিভিন্ন নিয়ন্ত্রণ বিন্দুগুলি বেছে নেওয়া প্রথাগত (ক্লাসিক্যাল) অনুকূলায়ক বা অপ্টিমাইজারের উপর নির্ভর করে অনুমান করতে হবে।
নতুন সেট নিয়ন্ত্রণ চয়ন করতে একটি প্রথাগত (ক্লাসিক্যাল) অনুকূলায়ক বা অপ্টিমাইজার ব্যবহার করুন।.
যতক্ষণনা \(C(\boldsymbol\theta)\) ন্যূনতমে পৌঁছে যায়, যা কিনা \(\boldsymbol\theta^*\) সমাধানের জন্য খুব কাছাকাছি, ততক্ষন চালিয়ে যান।
শেষ \(\boldsymbol\theta\) ব্যাবহার করুন \(\Big|\langle z_i\big|\psi(\boldsymbol\theta)\rangle\Big|^2\;\forall i\) বিতরণ থেকে অন্তিম নমুনা (স্যাম্পল) সমূহ উৎপন্ন করে,উত্তর পাওয়ার জন্যে।
অনেকগুলি পরামিতি রয়েছে সর্বত্র , উল্লেখযোগ্যভাবে ট্রায়াল ওয়েভফাংশন নির্বাচন। নীচে, আমরা বিবেচনা করি:
যেখানে:math:U_mathrm{entangler}`হ’ল সি-ফেজ(C-Phase) গেটস (সম্পূর্ণভাবে জড়িয়ে পড়ার গেটস) এবং:math:`U_mathrm{single}(theta) = prod_{i=1}^N Y(theta_{i}), যেখানে \(N`হল কুউবিট সংখ্যাা এবং: :math:`m\) হল কোয়ান্টাম বর্তনী (সার্কিট) গভীরতা।
আইসিং হ্যামিল্টোনীয়ান নির্মাণ করুন#
\(VRP\) দ্বিমিক (বাইনারি) পলিনমিয়াল বা বহুপদী অপটিমাইজেশন তৈরি করা যেতে পারে সাম্যতার সীমাবদ্ধতার সাথে শুধুমাত্র \(K=n-1\) অবস্থাগুলি বিবেচনা করে।এই ক্ষেত্রে উপ - ভ্রমণ অপসারণের সীমাবদ্ধতাগুলি প্রয়োজনীয় নয় এবং সমস্যাটি কেবল চল রাশি \({\bf z}\) উপর।বিশেষত, আমরা হিসাবে একটি বর্ধিত লাগরঙ্গিয়ান লিখতে পারি
যেখানে \(A\) একটি যথেষ্ট বড় পরামিতি।
হ্যামিল্টোনিয়ান থেকে কিউ.পি সূত্র#
ভেক্টরে \({\bf z}\) ক্ষেত্রে এবং একটি সম্পূর্ণ গ্রাফের জন্য (\(\delta(i)^+ = \delta(i)^- = \{0,1,\dots,i-1,i+1,\dots,n\}\)), \(H\) এই ভাবে লেখা যেতে পারে লেখা যেতে পারে।
সেটা হলো:
যেখানে: প্রথম পদ:
দ্বিতীয় পদ:
তৃতীয় পদ:
The QP formulation of the Ising Hamiltonian is ready for the use of VQE. We will solve the QP using optimization stack available in Qiskit optimization.
তথ্যসূত্র#
[1] E. Farhi, J. Goldstone, S. Gutmann e-print arXiv 1411.4028, 2014
[২] সর্বোচ্চ লাভ এবং ভ্রাম্যমান বিক্রেতার সমস্যা
[3] C. E. Miller, E. W. Tucker, and R. A. Zemlin (1960). "Integer Programming Formulations and Travelling Salesman Problems". J. ACM. 7: 326–329. doi:10.1145/321043.321046.
[4] D. L. Applegate, R. M. Bixby, V. Chvátal, and W. J. Cook (2006). The Traveling Salesman Problem. Princeton University Press, ISBN 978-0-691-12993-8.
আরম্ভ#
First of all we load all the packages that we need. CPLEX is required for the classical computations. You can install it by pip install 'qiskit-optimization[cplex]'.
[1]:
import numpy as np
import matplotlib.pyplot as plt
try:
import cplex
from cplex.exceptions import CplexError
except:
print("Warning: Cplex not found.")
import math
from qiskit_algorithms.utils import algorithm_globals
from qiskit_algorithms import SamplingVQE
from qiskit_algorithms.optimizers import SPSA
from qiskit.circuit.library import RealAmplitudes
from qiskit.primitives import Sampler
তারপরে আমরা চল রাশি গুলি আরম্ভ করব
[2]:
# Initialize the problem by defining the parameters
n = 3 # number of nodes + depot (n+1)
K = 2 # number of vehicles
আমরা একটি প্রারম্ভক শ্রেণীর সংজ্ঞা প্রদান করি যা এলোমেলোভাবে দ্বিমাত্রিক তালের উপর নোডগুলি রাখে এবং তাদের মধ্যে দূরত্ব গণনা করে।
[3]:
# Get the data
class Initializer:
def __init__(self, n):
self.n = n
def generate_instance(self):
n = self.n
# np.random.seed(33)
np.random.seed(1543)
xc = (np.random.rand(n) - 0.5) * 10
yc = (np.random.rand(n) - 0.5) * 10
instance = np.zeros([n, n])
for ii in range(0, n):
for jj in range(ii + 1, n):
instance[ii, jj] = (xc[ii] - xc[jj]) ** 2 + (yc[ii] - yc[jj]) ** 2
instance[jj, ii] = instance[ii, jj]
return xc, yc, instance
[4]:
# Initialize the problem by randomly generating the instance
initializer = Initializer(n)
xc, yc, instance = initializer.generate_instance()
প্রথাগত (ক্লাসিক্যাল) সমাধান IBM ILOG CPLEX ব্যাবহার করে।#
একটি প্রথাগত (ক্লাসিক্যাল) সমাধানের জন্য, আমরা আই.বি.এম আই.এল.ও.জি সি.পি.এল. ই.এক্স IBM ILOG CPLEX ব্যবহার করি। সি.পি.এল.ই.এক্স এই সমস্যার সঠিক সমাধান খুঁজে পেতে সক্ষম। আমরা প্রথমে একটি প্রথাগত (ক্লাসিক্যাল) অপ্টিমাইজার শ্রেণি সংজ্ঞায়িত করি যা এমনভাবে সমস্যাটিকে এনকোড করে যাতে সিপিএলএক্স সমাধান করতে পারে এবং তারপরে ক্লাসটি তাত্ক্ষণিক এবং সেটি সমাধান করে।
[5]:
class ClassicalOptimizer:
def __init__(self, instance, n, K):
self.instance = instance
self.n = n # number of nodes
self.K = K # number of vehicles
def compute_allowed_combinations(self):
f = math.factorial
return f(self.n) / f(self.K) / f(self.n - self.K)
def cplex_solution(self):
# refactoring
instance = self.instance
n = self.n
K = self.K
my_obj = list(instance.reshape(1, n**2)[0]) + [0.0 for x in range(0, n - 1)]
my_ub = [1 for x in range(0, n**2 + n - 1)]
my_lb = [0 for x in range(0, n**2)] + [0.1 for x in range(0, n - 1)]
my_ctype = "".join(["I" for x in range(0, n**2)]) + "".join(
["C" for x in range(0, n - 1)]
)
my_rhs = (
2 * ([K] + [1 for x in range(0, n - 1)])
+ [1 - 0.1 for x in range(0, (n - 1) ** 2 - (n - 1))]
+ [0 for x in range(0, n)]
)
my_sense = (
"".join(["E" for x in range(0, 2 * n)])
+ "".join(["L" for x in range(0, (n - 1) ** 2 - (n - 1))])
+ "".join(["E" for x in range(0, n)])
)
try:
my_prob = cplex.Cplex()
self.populatebyrow(my_prob, my_obj, my_ub, my_lb, my_ctype, my_sense, my_rhs)
my_prob.solve()
except CplexError as exc:
print(exc)
return
x = my_prob.solution.get_values()
x = np.array(x)
cost = my_prob.solution.get_objective_value()
return x, cost
def populatebyrow(self, prob, my_obj, my_ub, my_lb, my_ctype, my_sense, my_rhs):
n = self.n
prob.objective.set_sense(prob.objective.sense.minimize)
prob.variables.add(obj=my_obj, lb=my_lb, ub=my_ub, types=my_ctype)
prob.set_log_stream(None)
prob.set_error_stream(None)
prob.set_warning_stream(None)
prob.set_results_stream(None)
rows = []
for ii in range(0, n):
col = [x for x in range(0 + n * ii, n + n * ii)]
coef = [1 for x in range(0, n)]
rows.append([col, coef])
for ii in range(0, n):
col = [x for x in range(0 + ii, n**2, n)]
coef = [1 for x in range(0, n)]
rows.append([col, coef])
# Sub-tour elimination constraints:
for ii in range(0, n):
for jj in range(0, n):
if (ii != jj) and (ii * jj > 0):
col = [ii + (jj * n), n**2 + ii - 1, n**2 + jj - 1]
coef = [1, 1, -1]
rows.append([col, coef])
for ii in range(0, n):
col = [(ii) * (n + 1)]
coef = [1]
rows.append([col, coef])
prob.linear_constraints.add(lin_expr=rows, senses=my_sense, rhs=my_rhs)
[6]:
# Instantiate the classical optimizer class
classical_optimizer = ClassicalOptimizer(instance, n, K)
# Print number of feasible solutions
print("Number of feasible solutions = " + str(classical_optimizer.compute_allowed_combinations()))
Number of feasible solutions = 3.0
[7]:
# Solve the problem in a classical fashion via CPLEX
x = None
z = None
try:
x, classical_cost = classical_optimizer.cplex_solution()
# Put the solution in the z variable
z = [x[ii] for ii in range(n**2) if ii // n != ii % n]
# Print the solution
print(z)
except:
print("CPLEX may be missing.")
[1.0, 1.0, 1.0, 0.0, 1.0, 0.0]
[8]:
# Visualize the solution
def visualize_solution(xc, yc, x, C, n, K, title_str):
plt.figure()
plt.scatter(xc, yc, s=200)
for i in range(len(xc)):
plt.annotate(i, (xc[i] + 0.15, yc[i]), size=16, color="r")
plt.plot(xc[0], yc[0], "r*", ms=20)
plt.grid()
for ii in range(0, n**2):
if x[ii] > 0:
ix = ii // n
iy = ii % n
plt.arrow(
xc[ix],
yc[ix],
xc[iy] - xc[ix],
yc[iy] - yc[ix],
length_includes_head=True,
head_width=0.25,
)
plt.title(title_str + " cost = " + str(int(C * 100) / 100.0))
plt.show()
if x is not None:
visualize_solution(xc, yc, x, classical_cost, n, K, "Classical")
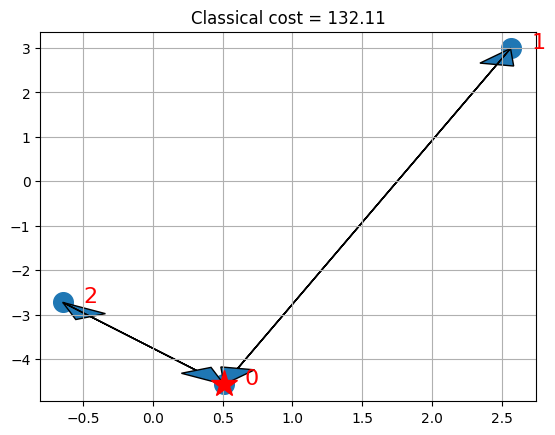
আপনার যদি সি.পি.এল.ই.এক্স থাকে তবে সমাধানটি তারাচিন্হ দিয়ে ডিপো এবং তীরচিন্হ সহ যানবাহনের জন্য নির্বাচিত রুটগুলি বা পথগুলি দেখায়।
স্থল থেকে কোয়ান্টাম সমাধান#
কোয়ান্টাম সমাধানের জন্য, আমরা ব্যবহার করি Qiskit
First, we derive the solution from the ground up, using a class QuantumOptimizer that encodes the quantum approach to solve the problem and then we instantiate it and solve it. We define the following methods inside the class:
binary_representation: encodes the problem \((M)\) into a QP terms (that’s basically linear algebra);construct_problem: constructs a QUBO optimization problem as an instance ofQuadraticProgram;solve_problem: solves the problem \((M)\) constructed at the previous step viaMinimunEigenOptimizerby usingSamplingVQEwith default parameters;
[9]:
from qiskit_optimization import QuadraticProgram
from qiskit_optimization.algorithms import MinimumEigenOptimizer
class QuantumOptimizer:
def __init__(self, instance, n, K):
self.instance = instance
self.n = n
self.K = K
def binary_representation(self, x_sol=0):
instance = self.instance
n = self.n
K = self.K
A = np.max(instance) * 100 # A parameter of cost function
# Determine the weights w
instance_vec = instance.reshape(n**2)
w_list = [instance_vec[x] for x in range(n**2) if instance_vec[x] > 0]
w = np.zeros(n * (n - 1))
for ii in range(len(w_list)):
w[ii] = w_list[ii]
# Some variables I will use
Id_n = np.eye(n)
Im_n_1 = np.ones([n - 1, n - 1])
Iv_n_1 = np.ones(n)
Iv_n_1[0] = 0
Iv_n = np.ones(n - 1)
neg_Iv_n_1 = np.ones(n) - Iv_n_1
v = np.zeros([n, n * (n - 1)])
for ii in range(n):
count = ii - 1
for jj in range(n * (n - 1)):
if jj // (n - 1) == ii:
count = ii
if jj // (n - 1) != ii and jj % (n - 1) == count:
v[ii][jj] = 1.0
vn = np.sum(v[1:], axis=0)
# Q defines the interactions between variables
Q = A * (np.kron(Id_n, Im_n_1) + np.dot(v.T, v))
# g defines the contribution from the individual variables
g = (
w
- 2 * A * (np.kron(Iv_n_1, Iv_n) + vn.T)
- 2 * A * K * (np.kron(neg_Iv_n_1, Iv_n) + v[0].T)
)
# c is the constant offset
c = 2 * A * (n - 1) + 2 * A * (K**2)
try:
max(x_sol)
# Evaluates the cost distance from a binary representation of a path
fun = (
lambda x: np.dot(np.around(x), np.dot(Q, np.around(x)))
+ np.dot(g, np.around(x))
+ c
)
cost = fun(x_sol)
except:
cost = 0
return Q, g, c, cost
def construct_problem(self, Q, g, c) -> QuadraticProgram:
qp = QuadraticProgram()
for i in range(n * (n - 1)):
qp.binary_var(str(i))
qp.objective.quadratic = Q
qp.objective.linear = g
qp.objective.constant = c
return qp
def solve_problem(self, qp):
algorithm_globals.random_seed = 10598
vqe = SamplingVQE(sampler=Sampler(), optimizer=SPSA(), ansatz=RealAmplitudes())
optimizer = MinimumEigenOptimizer(min_eigen_solver=vqe)
result = optimizer.solve(qp)
# compute cost of the obtained result
_, _, _, level = self.binary_representation(x_sol=result.x)
return result.x, level
ধাপ 1#
Instantiate the quantum optimizer class with parameters:
the instance;
the number of nodes and vehicles
nandK;
[10]:
# Instantiate the quantum optimizer class with parameters:
quantum_optimizer = QuantumOptimizer(instance, n, K)
ধাপ 2#
দ্বিমিক (বাইনারি) সুত্র বা গঠনের (আইএইচ-কিউপি) হিসাবে সমস্যাটি এনকোড করুন।
স্যানিটি বা সদ্বিবেচনা পরীক্ষা: নিশ্চিত করুন যে কোয়ান্টাম অপ্টিমাইজারে দ্বিমিক (বাইনারি) সূত্র বা গঠন সঠিক কিনা (যেমন, একই সমাধানের জন্যে একই ব্যয় হয়)।
[11]:
# Check if the binary representation is correct
try:
if z is not None:
Q, g, c, binary_cost = quantum_optimizer.binary_representation(x_sol=z)
print("Binary cost:", binary_cost, "classical cost:", classical_cost)
if np.abs(binary_cost - classical_cost) < 0.01:
print("Binary formulation is correct")
else:
print("Error in the binary formulation")
else:
print("Could not verify the correctness, due to CPLEX solution being unavailable.")
Q, g, c, binary_cost = quantum_optimizer.binary_representation()
print("Binary cost:", binary_cost)
except NameError as e:
print("Warning: Please run the cells above first.")
print(e)
Binary cost: 132.11148115684045 classical cost: 132.1114811568365
Binary formulation is correct
ধাপ 3#
সমস্যাটি Quadratic Program দৃষ্টান্ত (ইনস্ট্যান্স) হিসাবে এনকোড করুন
[12]:
qp = quantum_optimizer.construct_problem(Q, g, c)
ধাপ 4#
অপ্টিমাইজেশন স্ট্যাক থেকে ``MinimumEigenOptimizer``এর মাধ্যমে সমস্যার সমাধান করুন।কুইবিটের সংখ্যার উপর নির্ভর করে, অবস্থা-ভেক্টর সিমুলেশনটি কিছুটা সময় নিতে পারে; উদাহরণস্বরূপ, 12 কুইটসের সাথে এটি 12 ঘন্টােরও বেশি সময় নেয়। প্রোগ্রামটি কী করছে তা দেখতে লগিং দরকারী।
[13]:
quantum_solution, quantum_cost = quantum_optimizer.solve_problem(qp)
print(quantum_solution, quantum_cost)
[1. 1. 1. 0. 1. 0.] 132.11148115684045
ধাপ 5#
সমাধানটি দৃশ্যায়িত করা
[14]:
# Put the solution in a way that is compatible with the classical variables
x_quantum = np.zeros(n**2)
kk = 0
for ii in range(n**2):
if ii // n != ii % n:
x_quantum[ii] = quantum_solution[kk]
kk += 1
# visualize the solution
visualize_solution(xc, yc, x_quantum, quantum_cost, n, K, "Quantum")
# and visualize the classical for comparison
if x is not None:
visualize_solution(xc, yc, x, classical_cost, n, K, "Classical")
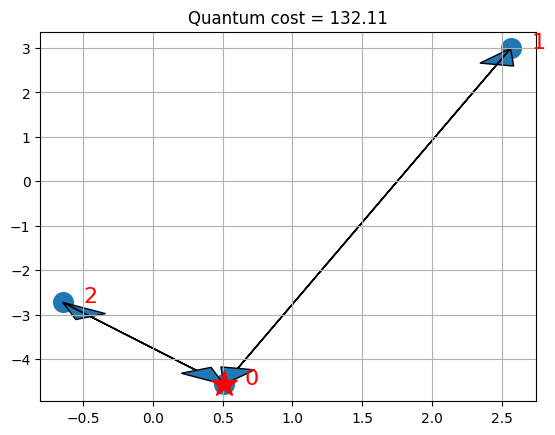
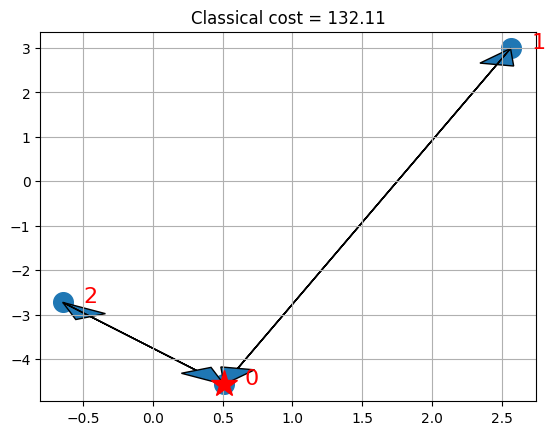
প্লটগুলি একটি তারা চিন্হ দিয়ে ডিপো এবং তীরচিন্হ গুলি সহকরে যানবাহনের জন্য নির্বাচিত রুটের উপস্থাপন করে। মনে রাখা দরকার যে এই বিশেষ ক্ষেত্রে, আমরা কিউ.পি গঠনের সর্বোত্তম সমাধানটি খুঁজে পেতে পারি, যা আই.এল.পি. র অনুকূল সমাধানের সাথে মিলে যায়।
মনে রাখতে হবে যে ভি.কিউ.ই হ’ল আইসিং হ্যামিল্টোনিয়ানএর কিউ.পি গঠনের বিষয়ে একটি হিউরিস্টিক তাত্ত্বিক কাজ।এ( A)- এর পছন্দের চয়নের জন্যে,কিউপি সূত্রের বা গঠনের স্থানীয় অনুকূলতা আইএলপির সম্ভাব্য সমাধান হবে। কিছু ছোট দৃষ্টান্ত (ইনস্ট্যান্স) জন্য, যেমন উপরে, আমরা কিউ.পি. গঠনের সর্বোত্তম সমাধানগুলি খুঁজে পেতে পারি যা আই.এল.পি. এর অনুকূলতার সাথে মিলে যায়, আই.এল.পি.র সর্বোত্তম সমাধানগুলি সন্ধান করা কিউপি গঠনের স্থানীয় অনুকূল সন্ধানের চেয়ে শক্ত, সাধারণভাবে, যা আবার আই.এল.পি.র সম্ভাব্য সমাধানগুলি খুঁজে পাওয়ার চেয়ে শক্ত। এমনকি ভি.কিউ.ই-র মধ্যে, কেউ নির্দিষ্ট পরিবর্তনশীল (ভ্যারিয়েশনাল)ফর্মের জন্য (ট্রায়াল ওয়েভ ফাংশন) আরও দৃঢ় প্রতিশ্রুত হতে পারে।
[15]:
import qiskit.tools.jupyter
%qiskit_version_table
%qiskit_copyright
Version Information
| Qiskit Software | Version |
|---|---|
qiskit-terra | 0.23.0 |
qiskit-aer | 0.11.1 |
qiskit-optimization | 0.5.0 |
qiskit-machine-learning | 0.6.0 |
| System information | |
| Python version | 3.9.15 |
| Python compiler | Clang 14.0.0 (clang-1400.0.29.102) |
| Python build | main, Oct 11 2022 22:27:25 |
| OS | Darwin |
| CPUs | 4 |
| Memory (Gb) | 16.0 |
| Tue Dec 06 21:53:30 2022 JST | |
This code is a part of Qiskit
© Copyright IBM 2017, 2022.
This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.
[ ]: