注釈

このページは docs/tutorials/03_ground_state_solvers.ipynb から生成されました。

基底状態ソルバー

はじめに

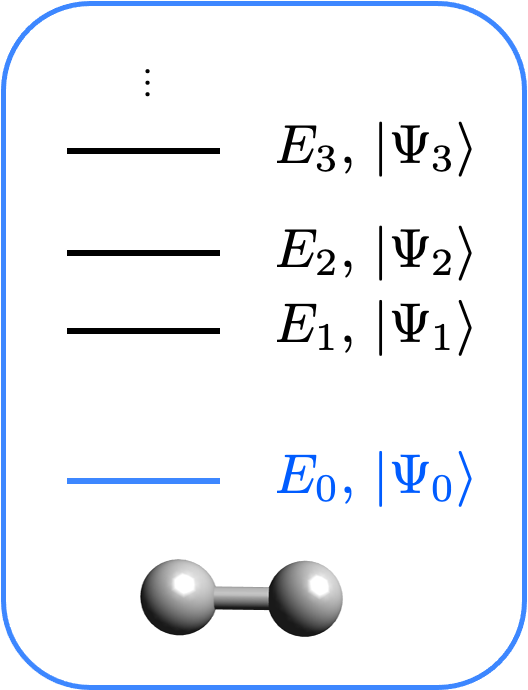
このチュートリアルでは、Qiskit Natureの基底状態計算インターフェースについて説明します。 目的は分子ハミルトニアンの基底状態を計算することです。 このハミルトニアンは、例えば電子的あるいは振動的なものである可能性があります。 ハミルトニアンの準備についての詳細は、 電子構造 と 振動構造のチュートリアル を参照してください。

電子的なケースでは、実際には純粋に**電子的**な部分を計算している、と言うべきでしょう。このチュートリアルで紹介するQiskit Natureスタックを使用する場合、核反発エネルギー*が自動的に追加され、**トータル の基底状態エネルギーが得られます。

まず分子系の定義から始めます。以下では、水素分子の電子部分を求めています。

from qiskit_nature.units import DistanceUnit
from qiskit_nature.second_q.drivers import PySCFDriver

driver = PySCFDriver(
    atom="H 0 0 0; H 0 0 0.735",
    basis="sto3g",
    charge=0,
    spin=0,
    unit=DistanceUnit.ANGSTROM,
)

es_problem = driver.run()

また、Jordan-Wignerマッピングを使う予定です。Qiskit Natureで利用できる様々なマッパーについてもっと知りたい方は、量子ビット空間への変換 をチェックしてください。

from qiskit_nature.second_q.mappers import JordanWignerMapper

mapper = JordanWignerMapper()

ソルバー

次に、ソルバーを定義する必要があります。ソルバーとは、基底状態を求めるアルゴリズムのことです。

まず、純粋に古典的な NumPyMinimumEigensolver の例から始めましょう。このアルゴリズムは、ハミルトニアンを正確に対角化します。これは規模の大きな問題には適用できませんが、小さな系で量子アルゴリズムの結果を確認するために用いることができます。

from qiskit.algorithms.minimum_eigensolvers import NumPyMinimumEigensolver

numpy_solver = NumPyMinimumEigensolver()

基底状態を見つけるために、変分量子固有ソルバー (VQE) アルゴリズムを用いることもできます。 VQE アルゴリズムは次の図に示すように、古典コンピューターと量子コンピューターの間で情報を交換することによって動作します。

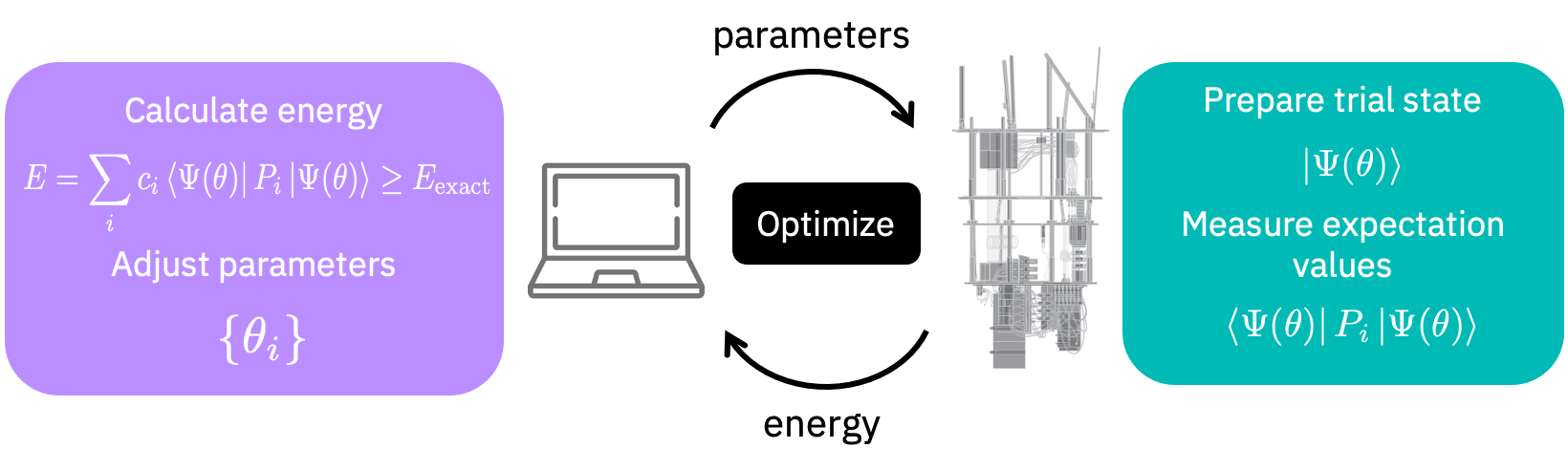
VQE ソルバーを初期化しましょう。

from qiskit.algorithms.minimum_eigensolvers import VQE
from qiskit.algorithms.optimizers import SLSQP
from qiskit.primitives import Estimator
from qiskit_nature.second_q.circuit.library import HartreeFock, UCCSD

ansatz = UCCSD(
    es_problem.num_spatial_orbitals,
    es_problem.num_particles,
    mapper,
    initial_state=HartreeFock(
        es_problem.num_spatial_orbitals,
        es_problem.num_particles,
        mapper,
    ),
)

vqe_solver = VQE(Estimator(), ansatz, SLSQP())
vqe_solver.initial_point = [0.0] * ansatz.num_parameters

VQE ソルバーを定義するには、3つの重要な要素が必要です。

1. Estimator primitive: これらはQiskit Terra 0.22の一部としてリリースされました。Primitiveについてもっと知りたい方は、このリソース をチェックしてください。

2. 変分形式：ここでは、Unitary Coupled Cluster (UCC) ansatzを使用します (例えば、[Physical Review A 98.2 (2018): 022322] を参照してください)。化学の標準であるため、UCCを用いたVQEの高速な初期化を可能にするファクトリーが既に利用可能です。デフォルトでは、すべての単励起と二重励起を使用します。ただし、励起タイプ (S, D, SD) や他のパラメーターを選択することができます。 また、解決しようとしている問題に応じて量子ビットの占有を初期化する HartreeFock 初期状態を UCCSD 変分形式の先頭に追加します。

3. オプティマイザー: これは変分形式のパラメーターを最適化する古典的なコードです。詳細は Qiskit Terraの関連ドキュメント を参照してください。

また、任意の利用可能なansatz / 初期状態を使用することもできますし、独自に定義することも可能です。以下にその例を示します。

from qiskit.algorithms.minimum_eigensolvers import VQE
from qiskit.circuit.library import TwoLocal

tl_circuit = TwoLocal(
    rotation_blocks=["h", "rx"],
    entanglement_blocks="cz",
    entanglement="full",
    reps=2,
    parameter_prefix="y",
)

another_solver = VQE(Estimator(), tl_circuit, SLSQP())

計算と結果

これで、問題の基底状態を計算するために、すべてをまとめる準備ができました。 mapper と量子アルゴリズムを一つの GroundStateEigensolver にラップする必要があります。

from qiskit_nature.second_q.algorithms import GroundStateEigensolver

calc = GroundStateEigensolver(mapper, vqe_solver)

これで、ワークフロー全体を見ることができます。1. 問題（ここでは es_problem ）に格納された第二量子化された演算子を生成します。 2. 演算子を量子ビット空間にマッピング (縮小の可能性もある) します。 3. 量子アルゴリズムファクトリー (例： Vqeuccfactory) を提供した場合、 problem に基づいてその設定を確定します。 4. ハミルトニアン量子ビット演算子で量子アルゴリズムを実行します。5. 収束したら、決定した基底状態での追加の観測量を評価します。

res = calc.solve(es_problem)
print(res)

=== GROUND STATE ENERGY ===

* Electronic ground state energy (Hartree): -1.857275030145
  - computed part:      -1.857275030145
~ Nuclear repulsion energy (Hartree): 0.719968994449
> Total ground state energy (Hartree): -1.137306035696

=== MEASURED OBSERVABLES ===

  0:  # Particles: 2.000 S: 0.000 S^2: 0.000 M: 0.000

=== DIPOLE MOMENTS ===

~ Nuclear dipole moment (a.u.): [0.0  0.0  1.3889487]

  0:
  * Electronic dipole moment (a.u.): [0.0  0.0  1.38894893]
    - computed part:      [0.0  0.0  1.38894893]
  > Dipole moment (a.u.): [0.0  0.0  -0.00000023]  Total: 0.00000023
                 (debye): [0.0  0.0  -0.00000058]  Total: 0.00000058

NumPy の正確なソルバーと比較して、VQE の結果が一致していることを確認できます。

calc = GroundStateEigensolver(mapper, numpy_solver)
res = calc.solve(es_problem)
print(res)

=== GROUND STATE ENERGY ===

* Electronic ground state energy (Hartree): -1.857275030202
  - computed part:      -1.857275030202
~ Nuclear repulsion energy (Hartree): 0.719968994449
> Total ground state energy (Hartree): -1.137306035753

=== MEASURED OBSERVABLES ===

  0:  # Particles: 2.000 S: 0.000 S^2: 0.000 M: 0.000

=== DIPOLE MOMENTS ===

~ Nuclear dipole moment (a.u.): [0.0  0.0  1.3889487]

  0:
  * Electronic dipole moment (a.u.): [0.0  0.0  1.3889487]
    - computed part:      [0.0  0.0  1.3889487]
  > Dipole moment (a.u.): [0.0  0.0  0.0]  Total: 0.0
                 (debye): [0.0  0.0  0.0]  Total: 0.0

フィルター関数の使用

ハミルトニアンの真の基底状態がヒルベルト空間の異なる対称性領域にあるため、そうした解に興味がないという場合もあります。こうした場合に NumPyEigensolver は、フィルター関数を取って、正しい粒子数をもつ固有状態だけを返すようにすることが可能です。これは特に、ハミルトニアンの真の基底状態が真空状態となる、振動構造計算の場合に重要です。粒子数をチェックするためのデフォルトのフィルター関数は、様々な問題に実装されており、以下のように用いることができます。

from qiskit.algorithms.minimum_eigensolvers import NumPyMinimumEigensolver
from qiskit_nature.second_q.drivers import GaussianForcesDriver
from qiskit_nature.second_q.mappers import DirectMapper
from qiskit_nature.second_q.problems import HarmonicBasis

driver = GaussianForcesDriver(logfile="aux_files/CO2_freq_B3LYP_631g.log")
basis = HarmonicBasis([2, 2, 2, 2])
vib_problem = driver.run(basis=basis)
vib_problem.hamiltonian.truncation_order = 2

mapper = DirectMapper()

solver_without_filter = NumPyMinimumEigensolver()
solver_with_filter = NumPyMinimumEigensolver(
    filter_criterion=vib_problem.get_default_filter_criterion()
)

gsc_wo = GroundStateEigensolver(mapper, solver_without_filter)
result_wo = gsc_wo.solve(vib_problem)

gsc_w = GroundStateEigensolver(mapper, solver_with_filter)
result_w = gsc_w.solve(vib_problem)

print(result_wo)
print("\n\n")
print(result_w)

=== GROUND STATE ===

* Vibrational ground state energy (cm^-1): -8e-12
The number of occupied modals for each mode is:
- Mode 0: 0.0
- Mode 1: 0.0
- Mode 2: 0.0
- Mode 3: 0.0



=== GROUND STATE ===

* Vibrational ground state energy (cm^-1): 2432.106954036546
The number of occupied modals for each mode is:
- Mode 0: 1.0
- Mode 1: 1.0
- Mode 2: 1.0
- Mode 3: 1.0

import qiskit.tools.jupyter

%qiskit_version_table
%qiskit_copyright

Version Information

Qiskit Software	Version
qiskit-terra	0.24.0.dev0+2b3686f
qiskit-aer	0.11.2
qiskit-ibmq-provider	0.19.2
qiskit-nature	0.6.0
System information
Python version	3.9.16
Python compiler	GCC 12.2.1 20221121 (Red Hat 12.2.1-4)
Python build	main, Dec 7 2022 00:00:00
OS	Linux
CPUs	8
Memory (Gb)	62.50002670288086
Thu Apr 06 08:55:38 2023 CEST

This code is a part of Qiskit

© Copyright IBM 2017, 2023.

This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.

Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.