Note
This page was generated from docs/tutorials/00_amplitude_estimation.ipynb.
Quantum Amplitude Estimation#
Given an operator \(\mathcal{A}\) that acts as
Quantum Amplitude Estimation (QAE) is the task of finding an estimate for the amplitude \(a\) of the state \(|\Psi_1\rangle\):
This task has first been investigated by Brassard et al. [1] in 2000 and their algorithm uses a combination of the Grover operator
where \(\mathcal{S}_0\) and \(\mathcal{S}_{\Psi_1}\) are reflections about the \(|0\rangle\) and \(|\Psi_1\rangle\) states, respectively, and phase estimation. However this algorithm, called AmplitudeEstimation in Qiskit Algorithms, requires large circuits and is computationally expensive. Therefore, other variants of QAE have been proposed, which we will showcase in this tutorial for a simple example.
In our example, \(\mathcal{A}\) describes a Bernoulli random variable with (assumed to be unknown) success probability \(p\):
On a quantum computer, we can model this operator with a rotation around the \(Y\)-axis of a single qubit
The Grover operator for this case is particularly simple
whose powers are very easy to calculate: \(\mathcal{Q}^k = R_Y(2k\theta_p)\).
We’ll fix the probability we want to estimate to \(p = 0.2\).
[1]:
p = 0.2
Now we can define circuits for \(\mathcal{A}\) and \(\mathcal{Q}\).
[2]:
import numpy as np
from qiskit.circuit import QuantumCircuit
class BernoulliA(QuantumCircuit):
"""A circuit representing the Bernoulli A operator."""
def __init__(self, probability):
super().__init__(1) # circuit on 1 qubit
theta_p = 2 * np.arcsin(np.sqrt(probability))
self.ry(theta_p, 0)
class BernoulliQ(QuantumCircuit):
"""A circuit representing the Bernoulli Q operator."""
def __init__(self, probability):
super().__init__(1) # circuit on 1 qubit
self._theta_p = 2 * np.arcsin(np.sqrt(probability))
self.ry(2 * self._theta_p, 0)
def power(self, k):
# implement the efficient power of Q
q_k = QuantumCircuit(1)
q_k.ry(2 * k * self._theta_p, 0)
return q_k
[3]:
A = BernoulliA(p)
Q = BernoulliQ(p)
Amplitude Estimation workflow#
Qiskit Algorithms implements several QAE algorithms that all derive from the AmplitudeEstimator interface. In the initializer we specify algorithm specific settings and the estimate method, which does all the work, takes an EstimationProblem as input and returns an
AmplitudeEstimationResult object. Since all QAE variants follow the same interface, we can use them all to solve the same problem instance.
Next, we’ll run all different QAE algorithms. To do so, we first define the estimation problem which will contain the \(\mathcal{A}\) and \(\mathcal{Q}\) operators as well as how to identify the \(|\Psi_1\rangle\) state, which in this simple example is just \(|1\rangle\).
[4]:
from qiskit_algorithms import EstimationProblem
problem = EstimationProblem(
state_preparation=A, # A operator
grover_operator=Q, # Q operator
objective_qubits=[0], # the "good" state Psi1 is identified as measuring |1> in qubit 0
)
To execute circuits we’ll use Sampler.
[5]:
from qiskit.primitives import Sampler
sampler = Sampler()
Canonical AE#
Now let’s solve this with the original QAE implementation by Brassard et al. [1].
[6]:
from qiskit_algorithms import AmplitudeEstimation
ae = AmplitudeEstimation(
num_eval_qubits=3, # the number of evaluation qubits specifies circuit width and accuracy
sampler=sampler,
)
With the algorithm defined, we can call the estimate method and provide it with the problem to solve.
[7]:
ae_result = ae.estimate(problem)
The estimate is available in the estimation key:
[8]:
print(ae_result.estimation)
0.1464466
We see that this is not a very good estimate for our target of \(p=0.2\)! That’s due to the fact the canonical AE is restricted to a discrete grid, specified by the number of evaluation qubits:
[9]:
import matplotlib.pyplot as plt
# plot estimated values
gridpoints = list(ae_result.samples.keys())
probabilities = list(ae_result.samples.values())
plt.bar(gridpoints, probabilities, width=0.5 / len(probabilities))
plt.axvline(p, color="r", ls="--")
plt.xticks(size=15)
plt.yticks([0, 0.25, 0.5, 0.75, 1], size=15)
plt.title("Estimated Values", size=15)
plt.ylabel("Probability", size=15)
plt.xlabel(r"Amplitude $a$", size=15)
plt.ylim((0, 1))
plt.grid()
plt.show()
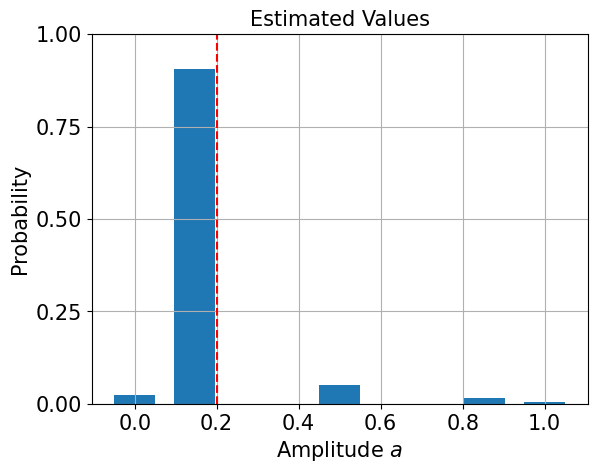
To improve the estimate we can interpolate the measurement probabilities and compute the maximum likelihood estimator that produces this probability distribution:
[10]:
print("Interpolated MLE estimator:", ae_result.mle)
Interpolated MLE estimator: 0.19999999403255486
We can have a look at the circuit that AE executes:
[11]:
ae_circuit = ae.construct_circuit(problem)
ae_circuit.decompose().draw(
"mpl", style="clifford"
) # decompose 1 level: exposes the Phase estimation circuit!
[11]:
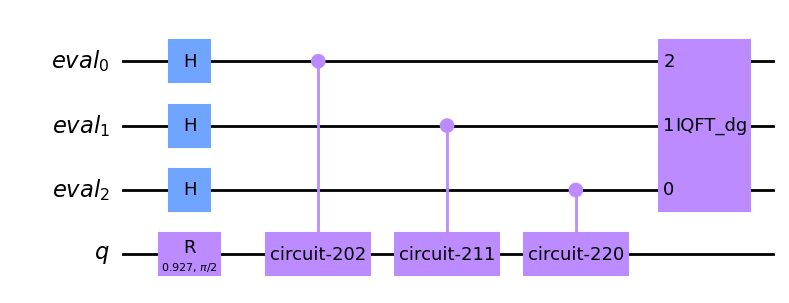
[12]:
from qiskit import transpile
basis_gates = ["h", "ry", "cry", "cx", "ccx", "p", "cp", "x", "s", "sdg", "y", "t", "cz"]
transpile(ae_circuit, basis_gates=basis_gates, optimization_level=2).draw("mpl", style="clifford")
[12]:
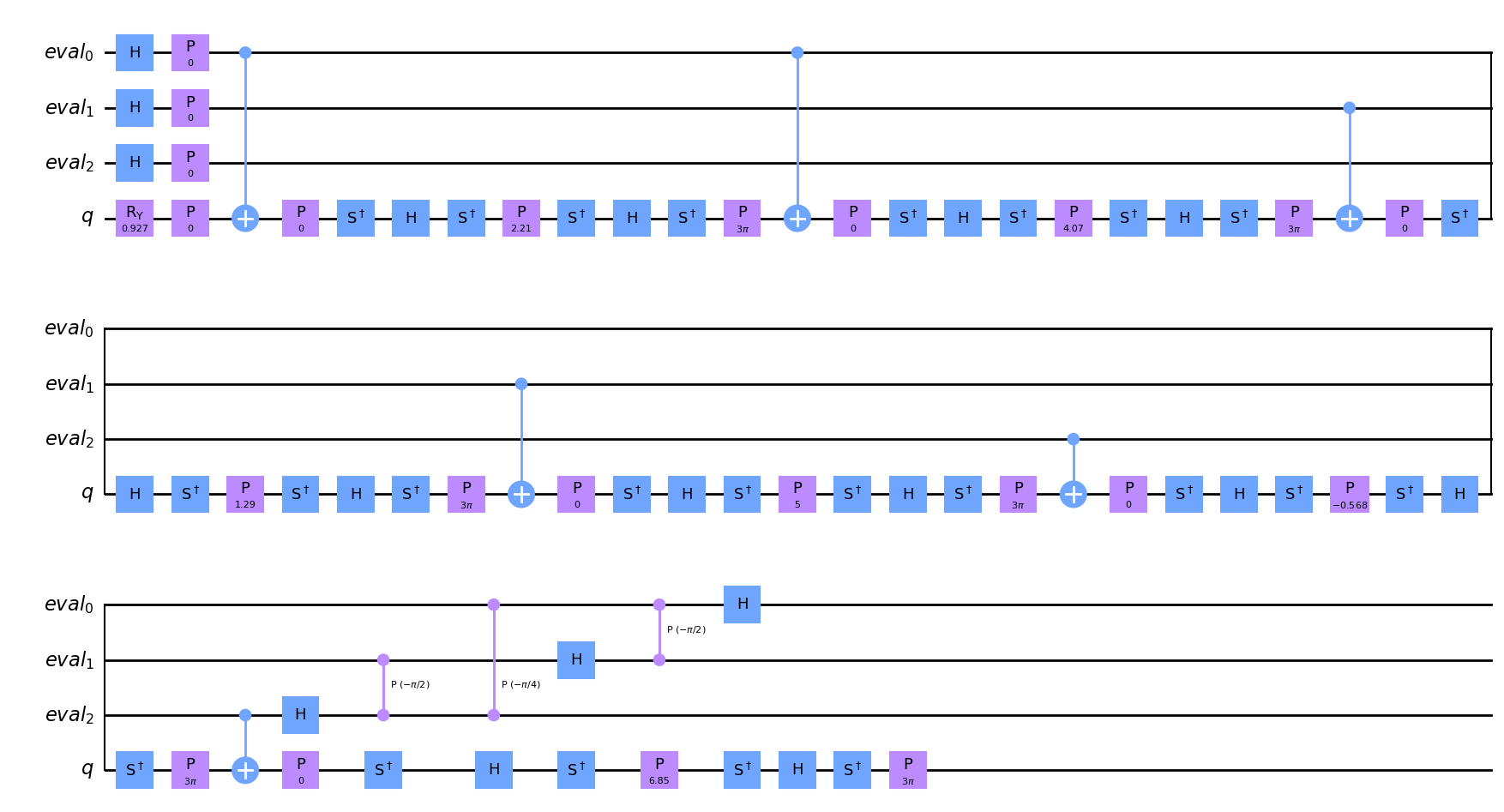
Iterative Amplitude Estimation#
See [2].
[13]:
from qiskit_algorithms import IterativeAmplitudeEstimation
iae = IterativeAmplitudeEstimation(
epsilon_target=0.01, # target accuracy
alpha=0.05, # width of the confidence interval
sampler=sampler,
)
iae_result = iae.estimate(problem)
print("Estimate:", iae_result.estimation)
Estimate: 0.2
The circuits here only consist of Grover powers and are much cheaper!
[14]:
iae_circuit = iae.construct_circuit(problem, k=3)
iae_circuit.draw("mpl", style="clifford")
[14]:
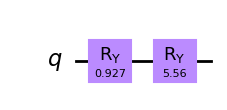
Maximum Likelihood Amplitude Estimation#
See [3].
[15]:
from qiskit_algorithms import MaximumLikelihoodAmplitudeEstimation
mlae = MaximumLikelihoodAmplitudeEstimation(
evaluation_schedule=3, # log2 of the maximal Grover power
sampler=sampler,
)
mlae_result = mlae.estimate(problem)
print("Estimate:", mlae_result.estimation)
Estimate: 0.20002237175368104
Faster Amplitude Estimation#
See [4].
[16]:
from qiskit_algorithms import FasterAmplitudeEstimation
fae = FasterAmplitudeEstimation(
delta=0.01, # target accuracy
maxiter=3, # determines the maximal power of the Grover operator
sampler=sampler,
)
fae_result = fae.estimate(problem)
print("Estimate:", fae_result.estimation)
Estimate: 0.2033710811456324
/opt/hostedtoolcache/Python/3.8.18/x64/lib/python3.8/site-packages/qiskit_algorithms/amplitude_estimators/estimation_problem.py:214: UserWarning: Rescaling discards the Grover operator.
warnings.warn("Rescaling discards the Grover operator.")
References#
[1] Quantum Amplitude Amplification and Estimation. Brassard et al (2000). https://arxiv.org/abs/quant-ph/0005055
[2] Iterative Quantum Amplitude Estimation. Grinko, D., Gacon, J., Zoufal, C., & Woerner, S. (2019). https://arxiv.org/abs/1912.05559
[3] Amplitude Estimation without Phase Estimation. Suzuki, Y., Uno, S., Raymond, R., Tanaka, T., Onodera, T., & Yamamoto, N. (2019). https://arxiv.org/abs/1904.10246
[4] Faster Amplitude Estimation. K. Nakaji (2020). https://arxiv.org/pdf/2003.02417.pdf
[17]:
import tutorial_magics
%qiskit_version_table
%qiskit_copyright
Version Information
| Software | Version |
|---|---|
qiskit | 1.0.1 |
qiskit_algorithms | 0.3.0 |
qiskit_aer | 0.13.3 |
| System information | |
| Python version | 3.8.18 |
| OS | Linux |
| Thu Feb 29 03:05:54 2024 UTC | |
This code is a part of a Qiskit project
© Copyright IBM 2017, 2024.
This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.
[ ]: