注釈
このページは docs/tutorials/06_basket_option_pricing.ipynb から生成されました。
バスケット・オプションの価格推定#
はじめに#
権利行使価格 \(K\) で、2つの原資産の満期時のスポット価格 \(S_T^1\), \(S_T^2\) がある確率分布に従うバスケット・オプションを考えます。その時のペイオフ関数は次のように定義されます:
以下では、振幅推定に基づく量子アルゴリズムを使用して、期待されるペイオフ、すなわちオプションの割引前の適正価格を見積もります。
目的関数の近似と量子コンピューターによる一般的なオプション価格設定とリスク分析は、以下の論文で紹介されています。
[1]:
import matplotlib.pyplot as plt
from scipy.interpolate import griddata
%matplotlib inline
import numpy as np
from qiskit import QuantumRegister, QuantumCircuit, AncillaRegister, transpile
from qiskit_algorithms import IterativeAmplitudeEstimation, EstimationProblem
from qiskit.circuit.library import WeightedAdder, LinearAmplitudeFunction
from qiskit_aer.primitives import Sampler
from qiskit_finance.circuit.library import LogNormalDistribution
不確実性モデル#
多変量対数正規ランダム分布を \(n\) 量子ビットの量子状態にロードする回路を構築します。 すべての次元 \(j = 1,\ldots,d\) について、分布は指定された区間 \([\text{low}_j, \text{high}_j]\) に切り捨てられ、 \(2^{n_j}\) グリッドポイントを使用して離散化されます。ここで、 \(n_j\) は次元 \(j\) を表すために使用される量子ビットの数を示します。つまり \(n_1+\ldots+n_d = n\) です。 回路に対応するユニタリー演算子は、以下のように実装されます:
ここで \(p_{i_1\ldots i_d}\) は、切り捨てられ離散化された分布を与える確率を表し、 \(i_j\) はアフィン写像で得られた正しい区間です。
簡単のため、株価はどちらも独立同分布とします。この仮定は以下のパラメーター化を単純にするだけのものであり、より複雑で相関のある多変量分布に容易に緩和することができます。現在の実装で唯一の重要な仮定は、異なる次元の離散化グリッドが同じステップサイズであるということです。
[2]:
# number of qubits per dimension to represent the uncertainty
num_uncertainty_qubits = 2
# parameters for considered random distribution
S = 2.0 # initial spot price
vol = 0.4 # volatility of 40%
r = 0.05 # annual interest rate of 4%
T = 40 / 365 # 40 days to maturity
# resulting parameters for log-normal distribution
mu = (r - 0.5 * vol**2) * T + np.log(S)
sigma = vol * np.sqrt(T)
mean = np.exp(mu + sigma**2 / 2)
variance = (np.exp(sigma**2) - 1) * np.exp(2 * mu + sigma**2)
stddev = np.sqrt(variance)
# lowest and highest value considered for the spot price; in between, an equidistant discretization is considered.
low = np.maximum(0, mean - 3 * stddev)
high = mean + 3 * stddev
# map to higher dimensional distribution
# for simplicity assuming dimensions are independent and identically distributed)
dimension = 2
num_qubits = [num_uncertainty_qubits] * dimension
low = low * np.ones(dimension)
high = high * np.ones(dimension)
mu = mu * np.ones(dimension)
cov = sigma**2 * np.eye(dimension)
# construct circuit
u = LogNormalDistribution(num_qubits=num_qubits, mu=mu, sigma=cov, bounds=list(zip(low, high)))
[3]:
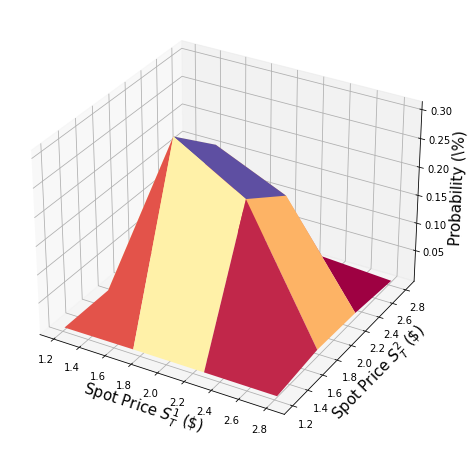
# plot PDF of uncertainty model
x = [v[0] for v in u.values]
y = [v[1] for v in u.values]
z = u.probabilities
# z = map(float, z)
# z = list(map(float, z))
resolution = np.array([2**n for n in num_qubits]) * 1j
grid_x, grid_y = np.mgrid[min(x) : max(x) : resolution[0], min(y) : max(y) : resolution[1]]
grid_z = griddata((x, y), z, (grid_x, grid_y))
plt.figure(figsize=(10, 8))
ax = plt.axes(projection="3d")
ax.plot_surface(grid_x, grid_y, grid_z, cmap=plt.cm.Spectral)
ax.set_xlabel("Spot Price $S_T^1$ (\$)", size=15)
ax.set_ylabel("Spot Price $S_T^2$ (\$)", size=15)
ax.set_zlabel("Probability (\%)", size=15)
plt.show()
ペイオフ関数#
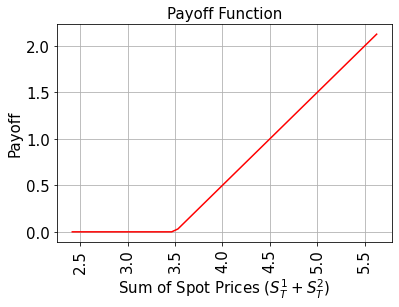
ペイオフ関数は、満期時のスポット価格合計 \((S_T^1 + S_T^2)\) がストライクプライス \(K\) よりも小さい間ゼロであり、その後線形に増加します。実装は、はじめに加重合計演算子で補助量子ビットにスポット価格の合計を計算し、その後コンパレーターを使用して、もし \((S_T^1 + S_T^2) \geq K\) ならば補助量子ビットを \(\big|0\rangle\) から \(\big|1\rangle\) にフリップします。この補助量子ビットはペイオフ関数の線形部分を制御するのに使われます。
線形部分自体は次のように近似されます。 小さい \(|y|\) に対して \(\sin^2(y + \pi/4) \approx y + 1/2\) という事実を利用します。 したがって、与えられた近似再スケーリング係数 \(c_\text{approx} \in [0, 1]\) および \(x \in [0, 1]\) に対して、次を考えます。
ここで、\(c_\text{approx}\) は十分小さいものとします。
次のように機能する演算子を簡単に構築できます
制御 Y-回転を用います。
最終的には、 \(\sin^2(a*x+b)\) に対応する最後の量子ビットで \(\big|1\rangle\) を測定する確率に関心があります。 上記の近似と合わせて、対象の値を近似できます。小さい \(c_\text{approx}\) を選択するほど、近似は良くなります。 ただし、 \(c_\text{approx}\) でスケーリングされたプロパティを推定しているため、それに応じて評価量子ビットの数 \(m\) を調整する必要があります。
近似の詳細については、次を参照してください: Quantum Risk Analysis. Woerner, Egger. 2018.
(現在実装中の) 加重合計演算子は整数のみを合計することができるため、結果を推定するために元の範囲から表現可能な範囲に写像し、結果を解釈する前に逆写像する必要があります。このマッピングは不確定性モデルのコンテキストに出てきたアフィン写像に一致します。
[4]:
# determine number of qubits required to represent total loss
weights = []
for n in num_qubits:
for i in range(n):
weights += [2**i]
# create aggregation circuit
agg = WeightedAdder(sum(num_qubits), weights)
n_s = agg.num_sum_qubits
n_aux = agg.num_qubits - n_s - agg.num_state_qubits # number of additional qubits
[5]:
# set the strike price (should be within the low and the high value of the uncertainty)
strike_price = 3.5
# map strike price from [low, high] to {0, ..., 2^n-1}
max_value = 2**n_s - 1
low_ = low[0]
high_ = high[0]
mapped_strike_price = (
(strike_price - dimension * low_) / (high_ - low_) * (2**num_uncertainty_qubits - 1)
)
# set the approximation scaling for the payoff function
c_approx = 0.25
# setup piecewise linear objective fcuntion
breakpoints = [0, mapped_strike_price]
slopes = [0, 1]
offsets = [0, 0]
f_min = 0
f_max = 2 * (2**num_uncertainty_qubits - 1) - mapped_strike_price
basket_objective = LinearAmplitudeFunction(
n_s,
slopes,
offsets,
domain=(0, max_value),
image=(f_min, f_max),
rescaling_factor=c_approx,
breakpoints=breakpoints,
)
[6]:
# define overall multivariate problem
qr_state = QuantumRegister(u.num_qubits, "state") # to load the probability distribution
qr_obj = QuantumRegister(1, "obj") # to encode the function values
ar_sum = AncillaRegister(n_s, "sum") # number of qubits used to encode the sum
ar = AncillaRegister(max(n_aux, basket_objective.num_ancillas), "work") # additional qubits
objective_index = u.num_qubits
basket_option = QuantumCircuit(qr_state, qr_obj, ar_sum, ar)
basket_option.append(u, qr_state)
basket_option.append(agg, qr_state[:] + ar_sum[:] + ar[:n_aux])
basket_option.append(basket_objective, ar_sum[:] + qr_obj[:] + ar[: basket_objective.num_ancillas])
print(basket_option.draw())
print("objective qubit index", objective_index)
┌───────┐┌────────┐
state_0: ┤0 ├┤0 ├──────
│ ││ │
state_1: ┤1 ├┤1 ├──────
│ P(X) ││ │
state_2: ┤2 ├┤2 ├──────
│ ││ │
state_3: ┤3 ├┤3 ├──────
└───────┘│ │┌────┐
obj: ─────────┤ ├┤3 ├
│ ││ │
sum_0: ─────────┤4 adder ├┤0 ├
│ ││ │
sum_1: ─────────┤5 ├┤1 ├
│ ││ │
sum_2: ─────────┤6 ├┤2 F ├
│ ││ │
work_0: ─────────┤7 ├┤4 ├
│ ││ │
work_1: ─────────┤8 ├┤5 ├
│ ││ │
work_2: ─────────┤9 ├┤6 ├
└────────┘└────┘
objective qubit index 4
[7]:
# plot exact payoff function (evaluated on the grid of the uncertainty model)
x = np.linspace(sum(low), sum(high))
y = np.maximum(0, x - strike_price)
plt.plot(x, y, "r-")
plt.grid()
plt.title("Payoff Function", size=15)
plt.xlabel("Sum of Spot Prices ($S_T^1 + S_T^2)$", size=15)
plt.ylabel("Payoff", size=15)
plt.xticks(size=15, rotation=90)
plt.yticks(size=15)
plt.show()
[8]:
# evaluate exact expected value
sum_values = np.sum(u.values, axis=1)
exact_value = np.dot(
u.probabilities[sum_values >= strike_price],
sum_values[sum_values >= strike_price] - strike_price,
)
print("exact expected value:\t%.4f" % exact_value)
exact expected value: 0.4870
期待ペイオフの評価#
我々は、まず量子回路を検証します。シミュレートで目的量子ビットの \(|1\rangle\) 状態の観測確率を分析します。
[9]:
num_state_qubits = basket_option.num_qubits - basket_option.num_ancillas
print("state qubits: ", num_state_qubits)
transpiled = transpile(basket_option, basis_gates=["u", "cx"])
print("circuit width:", transpiled.width())
print("circuit depth:", transpiled.depth())
state qubits: 5
circuit width: 11
circuit depth: 415
[10]:
basket_option_measure = basket_option.measure_all(inplace=False)
sampler = Sampler()
job = sampler.run(basket_option_measure)
[11]:
# evaluate the result
value = 0
probabilities = job.result().quasi_dists[0].binary_probabilities()
for i, prob in probabilities.items():
if prob > 1e-4 and i[-num_state_qubits:][0] == "1":
value += prob
# map value to original range
mapped_value = (
basket_objective.post_processing(value) / (2**num_uncertainty_qubits - 1) * (high_ - low_)
)
print("Exact Operator Value: %.4f" % value)
print("Mapped Operator value: %.4f" % mapped_value)
print("Exact Expected Payoff: %.4f" % exact_value)
Exact Operator Value: 0.4209
Mapped Operator value: 0.6350
Exact Expected Payoff: 0.4870
次に、振幅推定を使用して期待ペイオフを推定します。
[12]:
# set target precision and confidence level
epsilon = 0.01
alpha = 0.05
problem = EstimationProblem(
state_preparation=basket_option,
objective_qubits=[objective_index],
post_processing=basket_objective.post_processing,
)
# construct amplitude estimation
ae = IterativeAmplitudeEstimation(
epsilon_target=epsilon, alpha=alpha, sampler=Sampler(run_options={"shots": 100, "seed": 75})
)
[13]:
result = ae.estimate(problem)
[14]:
conf_int = (
np.array(result.confidence_interval_processed)
/ (2**num_uncertainty_qubits - 1)
* (high_ - low_)
)
print("Exact value: \t%.4f" % exact_value)
print(
"Estimated value: \t%.4f"
% (result.estimation_processed / (2**num_uncertainty_qubits - 1) * (high_ - low_))
)
print("Confidence interval:\t[%.4f, %.4f]" % tuple(conf_int))
Exact value: 0.4870
Estimated value: 0.4945
Confidence interval: [0.4821, 0.5069]
[15]:
import qiskit.tools.jupyter
%qiskit_version_table
%qiskit_copyright
Version Information
| Software | Version |
|---|---|
qiskit | None |
qiskit-terra | 0.45.0.dev0+c626be7 |
qiskit_finance | 0.4.0 |
qiskit_ibm_provider | 0.6.1 |
qiskit_aer | 0.12.0 |
qiskit_algorithms | 0.2.0 |
| System information | |
| Python version | 3.9.7 |
| Python compiler | GCC 7.5.0 |
| Python build | default, Sep 16 2021 13:09:58 |
| OS | Linux |
| CPUs | 2 |
| Memory (Gb) | 5.778430938720703 |
| Fri Aug 18 16:17:28 2023 EDT | |
This code is a part of Qiskit
© Copyright IBM 2017, 2023.
This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.
[ ]: