Nota
Esta página fue generada a partir de docs/tutorials/02_portfolio_diversification.ipynb.
Diversificación de Cartera#
Introducción#
En la gestión de activos, existen en general dos enfoques: gestión de inversiones activas y pasivas. Dentro de la gestión de inversiones pasivas, existen fondos de seguimiento de índices y existen enfoques basados en la diversificación de cartera, que tienen como objetivo representar una cartera con una gran cantidad de activos por una menor cantidad de acciones representativas. Este cuaderno ilustra un problema de diversificación de cartera, que recientemente se ha popularizado por dos razones: 1. Hace posible imitar el rendimiento de un índice (o un conjunto de activos igualmente grande) con un presupuesto limitado, con costos de transacción limitados. Es decir: el seguimiento de índices tradicional puede comprar todos los activos del índice, idealmente con las mismas ponderaciones que en el índice. Esto puede resultar poco práctico por varias razones: el total de incluso un solo lote de ronda por activo puede ascender a más que los activos bajo gestión, la gran escala del problema de seguimiento de índices con restricciones de integralidad puede dificultar el problema de optimización, y los costos de transacción del reequilibrio frecuente para ajustar las posiciones a las ponderaciones del índice pueden hacer que el enfoque sea costoso. Por lo tanto, un enfoque popular es seleccionar una cartera de \(q\) activos que representen el mercado con \(n\) activos, donde \(q\) es significativamente menor que \(n\), pero donde la cartera replica el comportamiento del mercado subyacente. Determinar cómo agrupar los activos en \(q\) conjuntos y cómo determinar cuáles \(q\) activos deben representar los \(q\) conjuntos equivale a resolver un problema de optimización a gran escala. A continuación, describimos el modelo matemático para el problema de la diversificación de cartera, tal como se presentó en [Cornuejols & Tutuncu, 2006] 2. Permite medidas de similitud entre series de tiempo más allá de la matriz de covarianza. Ten en cuenta que, tradicionalmente, la teoría de cartera moderna considera la matriz de covarianza como una medida de similitud entre los activos. Sin embargo, como tal, la matriz de covarianza es imperfecta. Considera, por ejemplo, una empresa que cotiza tanto en Londres como en Nueva York. Aunque ambos listados deberían ser muy similares, solo se superpondrán partes de la serie temporal de los precios de los dos listados, debido a la superposición parcial de las horas de apertura de los mercados. En lugar de la covarianza, se puede considerar, por ejemplo, la deformación dinámica temporal de [Berndt y Clifford, 1994] como una medida de similitud entre dos series de tiempo, lo que permite el hecho de que durante algunos períodos de tiempo, los datos son capturados por solo una serie de tiempo, mientras que para otras, ambas series de tiempo exhiben la similitud debido a la evolución paralela del precio de la acción.
El flujo de trabajo general que demostramos comprende:
elegir el conjunto básico de activos. En nuestro caso, se trata de una pequeña cantidad de acciones estadounidenses.
cargar la serie temporal que captura la evolución de los precios de los activos. En nuestro caso, se trata de una carga simplista de datos de precios de cierre diarios ajustados de Wikipedia o Nasdaq o LSE o EuroNext, mientras que en una gestión de activos real, se puede considerar una frecuencia mucho mayor.
calcular la similitud por pares entre las series temporales. En nuestro caso, ejecutamos una aproximación de tiempo lineal de la deformación dinámica temporal, todavía en la computadora clásica.
calcular la cartera real de \(q\) activos representativos, basándose en la medida de similitud. Este paso se ejecuta dos veces, en realidad. Primero, obtenemos un valor de referencia mediante la ejecución de un solucionador de IBM (el IBM ILOG CPLEX o el Exact Eigensolver) en la computadora clásica. En segundo lugar, ejecutamos un algoritmo híbrido alternativo parcialmente en la computadora cuántica.
visualización de los resultados. En nuestro caso, esta es nuevamente una gráfica simplista.
A continuación, explicamos primero el modelo utilizado en (4) arriba, antes de proceder con la instalación de los prerrequisitos previos y la carga de datos.
El Modelo#
Como se analiza en [Cornuejols & Tutuncu, 2006], describimos un modelo matemático que junta los activos en grupos similares y selecciona un activo representativo de cada grupo para incluirlo en la cartera de fondos indexados. El modelo se basa en los siguientes datos, que analizaremos con más detalle más adelante:
Por ejemplo, \(\rho_{ii} = 1\), \(\rho_{ij} \leq 1\) para \(i \neq j\) y \(\rho_{ij}\) es más grande para acciones más similares. Un ejemplo de esto es la correlación entre los rendimientos de las acciones \(i\) y \(j\). Pero se pueden elegir otros índices similares \(\rho_{ij}\).
El problema que nos interesa resolver es:
sujeto a la restricción de agrupamiento:
a las restricciones de consistencia:
y restricciones integrales:
Las variables \(y_j\) describen qué acciones \(j\) están en el fondo indexado (\(y_j = 1\) si \(j\) está seleccionado en el fondo, \(0\) de lo contrario). Para cada acción \(i = 1,\dots,n\), la variable \(x_{ij}\) indica qué acción \(j\) en el fondo indexado es más similar a \(i\) (\(x_{ij} = 1\) si \(j\) es la acción más similar en el fondo indexado, \(0\) en caso contrario).
La primera restricción selecciona \(q\) acciones en el fondo. La segunda restricción impone que cada acción \(i\) tiene exactamente una acción representativa \(j\) en el fondo. Las restricciones tercera y cuarta garantizan que la acción \(i\) puede ser representada por la acción \(j\) solo si \(j\) está en el fondo. El objetivo del modelo maximiza la similitud entre las \(n\) acciones y sus representantes en el fondo. También se pueden considerar diferentes funciones de costo.
Concatenamos las variables de decisión en un vector
cuya dimensión es \({\bf z} \in \{0,1\}^N\), con \(N = n (n+1)\) y denotamos la solución óptima con \({\bf z}^*\), y el costo óptimo \(f^*\).
Un Enfoque Híbrido#
Aquí, demostramos un enfoque que combina los pasos de la computación clásica y cuántica, siguiendo el enfoque de optimización aproximada cuántica de Farhi, Goldstone, y Gutmann (2014).
Construir una optimización polinomial binaria#
De \((M)\) se puede construir una optimización polinomial binaria con solamente restricciones de igualdad, sustituyendo las restricciones de desigualdad \(x_{ij} \leq y_j\) con las restricciones de igualdad equivalentes \(x_{ij} (1- y_j) = 0\). Entonces el problema se convierte en:
sujeto a la restricción de agrupamiento, las restricciones integrales y las siguientes restricciones de coherencia modificadas:
Construir el Hamiltoniano de Ising#
Ahora podemos construir el Hamiltoniano Ising (QUBO) mediante métodos de penalización (introduciendo un coeficiente de penalización \(A\) para cada restricción de igualdad) como
De la formulación Hamiltoniana a la Programación Cuadrática (QP)#
En el vector \({\bf z}\), los elementos Hamiltonianos de Ising se pueden reescribir de la siguiente manera,
Primer témino:
Segundo término:
Tercer término:
que es equivalente a:
Cuarto término:
Quinto término:
Por lo tanto, la formulación se convierte en,
que se puede pasar al solucionador propio variacional cuántico (variational quantum eigensolver).
Referencias#
[1] G. Cornuejols, M. L. Fisher, and G. L. Nemhauser, Location of bank accounts to optimize float: an analytical study of exact and approximate algorithms, Management Science, vol. 23(8), 1997
[2] E. Farhi, J. Goldstone, S. Gutmann e-print arXiv 1411.4028, 2014
[3] G. Cornuejols and R. Tutuncu, Optimization methods in finance, 2006
[4] DJ. Berndt and J. Clifford, Using dynamic time warping to find patterns in time series. In KDD workshop 1994 (Vol. 10, No. 16, pp. 359-370).
La implementación#
Primero, importamos los módulos necesarios.
[1]:
# Import requisite modules
import math
import datetime
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# Import Qiskit packages
from qiskit.circuit.library import TwoLocal
from qiskit_aer.primitives import Sampler
from qiskit_algorithms import NumPyMinimumEigensolver, QAOA, SamplingVQE
from qiskit_algorithms.optimizers import COBYLA
from qiskit_optimization.algorithms import MinimumEigenOptimizer
# The data providers of stock-market data
from qiskit_finance.data_providers import RandomDataProvider
from qiskit_finance.applications.optimization import PortfolioDiversification
A continuación, descargamos los datos de precios de dos acciones y calculamos su matriz de similitud por pares (distancia deformación dinámica temporal normalizada a (0,1] al tomar el recíproco). Si esto falla, por ejemplo, debido a que está fuera de línea o excede el límite diario de acceso a los datos del mercado de valores, consideramos una matriz constante en su lugar.
[2]:
# Generate a pairwise time-series similarity matrix
seed = 123
stocks = ["TICKER1", "TICKER2"]
n = len(stocks)
data = RandomDataProvider(
tickers=stocks,
start=datetime.datetime(2016, 1, 1),
end=datetime.datetime(2016, 1, 30),
seed=seed,
)
data.run()
rho = data.get_similarity_matrix()
Ahora decidimos el número de grupos. Tiene que ser menor que la cantidad de acciones que hemos cargado.
[3]:
q = 1 # q less or equal than n
Solución clásica usando IBM ILOG CPLEX#
Para una solución clásica, utilizamos IBM CPLEX. CPLEX puede encontrar la solución exacta de este problema. Primero definimos una clase ClassicalOptimizer que codifica el problema de una manera que CPLEX pueda resolver, y luego instanciamos la clase y la resolvemos.
[4]:
class ClassicalOptimizer:
def __init__(self, rho, n, q):
self.rho = rho
self.n = n # number of inner variables
self.q = q # number of required selection
def compute_allowed_combinations(self):
f = math.factorial
return int(f(self.n) / f(self.q) / f(self.n - self.q))
def cplex_solution(self):
# refactoring
rho = self.rho
n = self.n
q = self.q
my_obj = list(rho.reshape(1, n**2)[0]) + [0.0 for x in range(0, n)]
my_ub = [1 for x in range(0, n**2 + n)]
my_lb = [0 for x in range(0, n**2 + n)]
my_ctype = "".join(["I" for x in range(0, n**2 + n)])
my_rhs = (
[q]
+ [1 for x in range(0, n)]
+ [0 for x in range(0, n)]
+ [0.1 for x in range(0, n**2)]
)
my_sense = (
"".join(["E" for x in range(0, 1 + n)])
+ "".join(["E" for x in range(0, n)])
+ "".join(["L" for x in range(0, n**2)])
)
try:
my_prob = cplex.Cplex()
self.populatebyrow(my_prob, my_obj, my_ub, my_lb, my_ctype, my_sense, my_rhs)
my_prob.solve()
except CplexError as exc:
print(exc)
return
x = my_prob.solution.get_values()
x = np.array(x)
cost = my_prob.solution.get_objective_value()
return x, cost
def populatebyrow(self, prob, my_obj, my_ub, my_lb, my_ctype, my_sense, my_rhs):
n = self.n
prob.objective.set_sense(prob.objective.sense.minimize)
prob.variables.add(obj=my_obj, lb=my_lb, ub=my_ub, types=my_ctype)
prob.set_log_stream(None)
prob.set_error_stream(None)
prob.set_warning_stream(None)
prob.set_results_stream(None)
rows = []
col = [x for x in range(n**2, n**2 + n)]
coef = [1 for x in range(0, n)]
rows.append([col, coef])
for ii in range(0, n):
col = [x for x in range(0 + n * ii, n + n * ii)]
coef = [1 for x in range(0, n)]
rows.append([col, coef])
for ii in range(0, n):
col = [ii * n + ii, n**2 + ii]
coef = [1, -1]
rows.append([col, coef])
for ii in range(0, n):
for jj in range(0, n):
col = [ii * n + jj, n**2 + jj]
coef = [1, -1]
rows.append([col, coef])
prob.linear_constraints.add(lin_expr=rows, senses=my_sense, rhs=my_rhs)
[5]:
# Instantiate the classical optimizer class
classical_optimizer = ClassicalOptimizer(rho, n, q)
# Compute the number of feasible solutions:
print("Number of feasible combinations= " + str(classical_optimizer.compute_allowed_combinations()))
# Compute the total number of possible combinations (feasible + unfeasible)
print("Total number of combinations= " + str(2 ** (n * (n + 1))))
Number of feasible combinations= 2
Total number of combinations= 64
[6]:
# Visualize the solution
def visualize_solution(xc, yc, x, C, n, K, title_str):
plt.figure()
plt.scatter(xc, yc, s=200)
for i in range(len(xc)):
plt.annotate(i, (xc[i] + 0.015, yc[i]), size=16, color="r")
plt.grid()
for ii in range(n**2, n**2 + n):
if x[ii] > 0:
plt.plot(xc[ii - n**2], yc[ii - n**2], "r*", ms=20)
for ii in range(0, n**2):
if x[ii] > 0:
iy = ii // n
ix = ii % n
plt.plot([xc[ix], xc[iy]], [yc[ix], yc[iy]], "C2")
plt.title(title_str + " cost = " + str(int(C * 100) / 100.0))
plt.show()
La solución muestra las acciones seleccionadas a través de las estrellas y en verde los enlaces (a través de similitudes) con otras acciones que están representadas en el fondo por las acciones vinculadas.
Solución con Computación Cuántica usando Qiskit#
Para la solución cuántica, usamos Qiskit. Primero definimos una clase QuantumOptimizer que codifica el enfoque cuántico para resolver el problema y luego la instanciamos y la resolvemos. Definimos los siguientes métodos dentro de la clase:
exact_solution: para asegurarnos de que el Hamiltoniano de Ising está codificado correctamente en la base \(Z\), podemos calcular su descomposición propia de forma clásica, es decir, considerando una matriz simétrica de dimensión \(2^N \times 2^N\). Para el problema en cuestión \(n=3\), esto es \(N = 12\), parece ser el límite para muchas computadoras portátiles;sampling_vqe_solution: resuelve el problema \((M)\) a través del Solucionador Propio Variacional Cuántico de Muestreo (Sampling Variational Quantum Eigensolver,SamplingVQE);qaoa_solution: resuelve el problema \((M)\) a través de un Algoritmo Cuántico de Optimización Aproximada (Quantum Approximate Optimization Algorithm,QAOA).
[7]:
from qiskit_algorithms.utils import algorithm_globals
class QuantumOptimizer:
def __init__(self, rho, n, q):
self.rho = rho
self.n = n
self.q = q
self.pdf = PortfolioDiversification(similarity_matrix=rho, num_assets=n, num_clusters=q)
self.qp = self.pdf.to_quadratic_program()
# Obtains the least eigenvalue of the Hamiltonian classically
def exact_solution(self):
exact_mes = NumPyMinimumEigensolver()
exact_eigensolver = MinimumEigenOptimizer(exact_mes)
result = exact_eigensolver.solve(self.qp)
return self.decode_result(result)
def sampling_vqe_solution(self):
algorithm_globals.random_seed = 100
cobyla = COBYLA()
cobyla.set_options(maxiter=250)
ry = TwoLocal(n, "ry", "cz", reps=5, entanglement="full")
svqe_mes = SamplingVQE(sampler=Sampler(), ansatz=ry, optimizer=cobyla)
svqe = MinimumEigenOptimizer(svqe_mes)
result = svqe.solve(self.qp)
return self.decode_result(result)
def qaoa_solution(self):
algorithm_globals.random_seed = 1234
cobyla = COBYLA()
cobyla.set_options(maxiter=250)
qaoa_mes = QAOA(sampler=Sampler(), optimizer=cobyla, reps=3)
qaoa = MinimumEigenOptimizer(qaoa_mes)
result = qaoa.solve(self.qp)
return self.decode_result(result)
def decode_result(self, result, offset=0):
quantum_solution = 1 - (result.x)
ground_level = self.qp.objective.evaluate(result.x)
return quantum_solution, ground_level
Paso 1#
Crea una instancia de la clase del optimizador cuántico con los parámetros: - la matriz de similitud rho; - el número de activos y agrupaciones n y q;
[8]:
# Instantiate the quantum optimizer class with parameters:
quantum_optimizer = QuantumOptimizer(rho, n, q)
Paso 2#
Codifica el problema como una formulación binaria (IH-QP).
Comprobación: asegúrate de que la formulación binaria en el optimizador cuántico sea correcta (es decir, que produzca el mismo costo dada la misma solución).
[9]:
# Check if the binary representation is correct. This requires CPLEX
try:
import cplex
# warnings.filterwarnings('ignore')
quantum_solution, quantum_cost = quantum_optimizer.exact_solution()
print(quantum_solution, quantum_cost)
classical_solution, classical_cost = classical_optimizer.cplex_solution()
print(classical_solution, classical_cost)
if np.abs(quantum_cost - classical_cost) < 0.01:
print("Binary formulation is correct")
else:
print("Error in the formulation of the Hamiltonian")
except Exception as ex:
print(ex)
[0. 1. 0. 1. 0. 1.] 1.000779571614484
[1. 0. 1. 0. 1. 0.] 1.000779571614484
Binary formulation is correct
Paso 3#
Codifica el problema como un Hamiltoniano Ising en la base Z.
Comprobación: asegúrate de que la formulación sea correcta (es decir, que rinda el mismo costo con la misma solución)
[10]:
ground_state, ground_level = quantum_optimizer.exact_solution()
print(ground_state)
classical_cost = 1.000779571614484 # obtained from the CPLEX solution
try:
if np.abs(ground_level - classical_cost) < 0.01:
print("Ising Hamiltonian in Z basis is correct")
else:
print("Error in the Ising Hamiltonian formulation")
except Exception as ex:
print(ex)
[0. 1. 0. 1. 0. 1.]
Ising Hamiltonian in Z basis is correct
Paso 4#
Resolver el problema a través de SamplingVQE. Ten en cuenta que, dependiendo de la cantidad de qubits, esto puede llevar un tiempo: para 6 qubits se necesitan 15 minutos en una Macbook Pro 2015, para 12 qubits se necesitan más de 12 horas. Para ejecuciones más largas, el log puede ser útil para observar el funcionamiento; de lo contrario, solo tendrás que esperar hasta que se imprima la solución.
[11]:
svqe_state, svqe_level = quantum_optimizer.sampling_vqe_solution()
print(svqe_state, svqe_level)
try:
if np.linalg.norm(ground_state - svqe_state) < 0.01:
print("SamplingVQE produces the same solution as the exact eigensolver.")
else:
print(
"SamplingVQE does not produce the same solution as the exact eigensolver, but that is to be expected."
)
except Exception as ex:
print(ex)
[0. 1. 0. 1. 0. 1.] 1.000779571614484
SamplingVQE produces the same solution as the exact eigensolver.
Paso 5#
Visualiza la solución
[12]:
xc, yc = data.get_coordinates()
[13]:
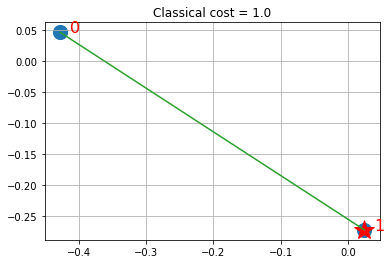
visualize_solution(xc, yc, ground_state, ground_level, n, q, "Classical")
[14]:
visualize_solution(xc, yc, svqe_state, svqe_level, n, q, "SamplingVQE")

La solución muestra las acciones seleccionadas usando estrellas y en verde los enlaces (a través de similitudes) con otras acciones que están representadas en el fondo por la acción vinculada. Sin embargo, toma en cuenta que SamplingVQE es un trabajo heurístico sobre la formulación QP del Hamiltoniano de Ising. Para las elecciones viables de A, los óptimos locales de la formulación del QP van a ser soluciones factibles para el ILP (integer linear program, o programación lineal en enteros). Mientras que para algunas pequeñas instancias, como se muestra arriba, podemos encontrar soluciones óptimas para la formulación QP que coinciden con los óptimos del ILP; en general, encontrar soluciones del ILP es más difícil que encontrar óptimos locales de la solución del QP. Aún dentro del SamplingVQE, uno puede proporcionar garantías más fuertes para formas variacionales específicas (funciones de onda de prueba).
[15]:
import qiskit.tools.jupyter
%qiskit_version_table
%qiskit_copyright
Version Information
| Software | Version |
|---|---|
qiskit | 0.45.0.dev0+ea871e0 |
qiskit_optimization | 0.6.0 |
qiskit_finance | 0.4.0 |
qiskit_algorithms | 0.3.0 |
qiskit_aer | 0.12.2 |
qiskit_ibm_provider | 0.7.0 |
| System information | |
| Python version | 3.9.7 |
| Python compiler | GCC 7.5.0 |
| Python build | default, Sep 16 2021 13:09:58 |
| OS | Linux |
| CPUs | 2 |
| Memory (Gb) | 5.7784271240234375 |
| Tue Sep 05 15:08:55 2023 EDT | |
This code is a part of Qiskit
© Copyright IBM 2017, 2023.
This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.
[ ]: