Note
This page was generated from docs/tutorials/05_admm_optimizer.ipynb.
ADMM Optimizer#
Introduction#
The ADMM Optimizer can solve classes of mixed-binary constrained optimization problems, hereafter (MBCO), which often appear in logistic, finance, and operation research. In particular, the ADMM Optimizer here designed can tackle the following optimization problem \((P)\):
subject to the constraints:
with the corresponding functional assumptions.
Function \(q: \mathbb{R}^n \to \mathbb{R}\) is quadratic, i.e., \(q(x) = x^{\intercal} Q x + a^{\intercal} x\) for a given symmetric squared matrix \(Q \in \mathbb{R}^n \times \mathbb{R}^n, Q = Q^{\intercal}\), and vector \(a \in \mathbb{R}^n\);
The set \(\mathcal{X} = \{0,1\}^n = \{x_{(i)} (1-x_{(i)}) = 0, \forall i\}\) enforces the binary constraints;
Matrix \(G\in\mathbb{R}^n \times \mathbb{R}^{n'}\), vector \(b \in \mathbb{R}^{n'}\), and function \(g: \mathbb{R}^n \to \mathbb{R}\) is convex;
Function \(\varphi: \mathbb{R}^l \to \mathbb{R}\) is convex and \(\mathcal{U}\) is a convex set;
Function \(\ell: \mathbb{R}^n\times \mathbb{R}^l \to \mathbb{R}\) is jointly convex in \(x, u\).
In order to solve MBO problems, [1] proposed heuristics for \((P)\) based on the Alternating Direction Method of Multipliers (ADMM) [2]. ADMM is an operator splitting algorithm with a long history in convex optimization, and it is known to have residual, objective and dual variable convergence properties, provided that convexity assumptions are holding.
The method of [1] (referred to as 3-ADMM-H) leverages the ADMM operator-splitting procedure to devise a decomposition for certain classes of MBOs into:
a QUBO subproblem to be solved by on the quantum device via variational algorithms, such as VQE or QAOA;
continuous convex constrained subproblem, which can be efficiently solved with classical optimization solvers.
The algorithm 3-ADMM-H works as follows:
Initialization phase (set the parameters and the QUBO and convex solvers);
For each ADMM iterations ($k = 1, 2, \ldots, $) until termination:
Solve a properly defined QUBO subproblem (with a classical or quantum solver);
Solve properly defined convex problems (with a classical solver);
Update the dual variables.
Return optimizers and cost.
A comprehensive discussion on the conditions for convergence, feasibility and optimality of the algorithm can be found in [1]. A variant with 2 ADMM blocks, namely a QUBO subproblem, and a continuous convex constrained subproblem, is also introduced in [1].
References#
Initialization#
First of all we load all the packages that we need.
[1]:
import matplotlib.pyplot as plt
from docplex.mp.model import Model
from qiskit_algorithms import QAOA, NumPyMinimumEigensolver
from qiskit_algorithms.optimizers import COBYLA
from qiskit.primitives import Sampler
from qiskit_optimization.algorithms import CobylaOptimizer, MinimumEigenOptimizer
from qiskit_optimization.algorithms.admm_optimizer import ADMMParameters, ADMMOptimizer
from qiskit_optimization.translators import from_docplex_mp
# If CPLEX is installed, you can uncomment this line to import the CplexOptimizer.
# CPLEX can be used in this tutorial to solve the convex continuous problem,
# but also as a reference to solve the QUBO, or even the full problem.
#
# from qiskit.optimization.algorithms import CplexOptimizer
We first initialize all the algorithms we plan to use later in this tutorial.
To solve the QUBO problems we can choose between
MinimumEigenOptimizerusing differentMinimumEigensolver, such asSamplingVQE,QAOAorNumpyMinimumEigensolver(classical)GroverOptimizerCplexOptimizer(classical, if CPLEX is installed)
and to solve the convex continuous problems we can choose between the following classical solvers:
CplexOptimizer(if CPLEX is installed)CobylaOptimizer
In case CPLEX is not available, the CobylaOptimizer (for convex continuous problems) and the MinimumEigenOptimizer using the NumpyMinimumEigensolver (for QUBOs) can be used as classical alternatives to CPLEX for testing, validation, and benchmarking.
[2]:
# define COBYLA optimizer to handle convex continuous problems.
cobyla = CobylaOptimizer()
# define QAOA via the minimum eigen optimizer
qaoa = MinimumEigenOptimizer(QAOA(sampler=Sampler(), optimizer=COBYLA()))
# exact QUBO solver as classical benchmark
exact = MinimumEigenOptimizer(NumPyMinimumEigensolver()) # to solve QUBOs
# in case CPLEX is installed it can also be used for the convex problems, the QUBO,
# or as a benchmark for the full problem.
#
# cplex = CplexOptimizer()
Example#
We test 3-ADMM-H algorithm on a simple Mixed-Binary Quadratic Problem with equality and inequality constraints (Example 6 reported in [1]). We first construct a docplex problem and then load it into a QuadraticProgram.
[3]:
# construct model using docplex
mdl = Model("ex6")
v = mdl.binary_var(name="v")
w = mdl.binary_var(name="w")
t = mdl.binary_var(name="t")
u = mdl.continuous_var(name="u")
mdl.minimize(v + w + t + 5 * (u - 2) ** 2)
mdl.add_constraint(v + 2 * w + t + u <= 3, "cons1")
mdl.add_constraint(v + w + t >= 1, "cons2")
mdl.add_constraint(v + w == 1, "cons3")
# load quadratic program from docplex model
qp = from_docplex_mp(mdl)
print(qp.prettyprint())
Problem name: ex6
Minimize
5*u^2 + t - 20*u + v + w + 20
Subject to
Linear constraints (3)
t + u + v + 2*w <= 3 'cons1'
t + v + w >= 1 'cons2'
v + w == 1 'cons3'
Continuous variables (1)
0 <= u
Binary variables (3)
v w t
Classical Solution#
3-ADMM-H needs a QUBO optimizer to solve the QUBO subproblem, and a continuous optimizer to solve the continuous convex constrained subproblem. We first solve the problem classically: we use the MinimumEigenOptimizer with the NumPyMinimumEigenSolver as a classical and exact QUBO solver and we use the CobylaOptimizer as a continuous convex solver. 3-ADMM-H supports any other suitable solver available in Qiskit optimization. For instance, SamplingVQE, QAOA, and
GroverOptimizer can be invoked as quantum solvers, as demonstrated later. If CPLEX is installed, the CplexOptimizer can also be used as both, a QUBO and convex solver.
Parameters#
The 3-ADMM-H are wrapped in class ADMMParameters. Customized parameter values can be set as arguments of the class. In this example, parameters \(\rho, \beta\) are initialized to \(1001\) and \(1000\), respectively. The penalization factor_c of equality constraints \(Gx = b\) is set to \(900\). The tolerance tol for primal residual convergence is set to 1.e-6. In this case, the 3-block implementation is guaranteed to converge for Theorem 4 of [1], because the
inequality constraint with the continuous variable is always active. The 2-block implementation can be run by setting three_block=False, and practically converges to a feasible not optimal solution.
[4]:
admm_params = ADMMParameters(
rho_initial=1001, beta=1000, factor_c=900, maxiter=100, three_block=True, tol=1.0e-6
)
Calling 3-ADMM-H algorithm#
To invoke the 3-ADMM-H algorithm, an instance of the ADMMOptimizer class needs to be created. This takes ADMM-specific parameters and the subproblem optimizers separately into the constructor. The solution returned is an instance of OptimizationResult class.
[5]:
# define QUBO optimizer
qubo_optimizer = exact
# qubo_optimizer = cplex # uncomment to use CPLEX instead
# define classical optimizer
convex_optimizer = cobyla
# convex_optimizer = cplex # uncomment to use CPLEX instead
# initialize ADMM with classical QUBO and convex optimizer
admm = ADMMOptimizer(
params=admm_params, qubo_optimizer=qubo_optimizer, continuous_optimizer=convex_optimizer
)
[6]:
# run ADMM to solve problem
result = admm.solve(qp)
Classical Solver Result#
The 3-ADMM-H solution can be then printed and visualized. The x attribute of the solution contains respectively, the values of the binary decision variables and the values of the continuous decision variables. The fval is the objective value of the solution.
[7]:
print(result.prettyprint())
objective function value: 1.0
variable values: v=1.0, w=0.0, t=0.0, u=2.0
status: SUCCESS
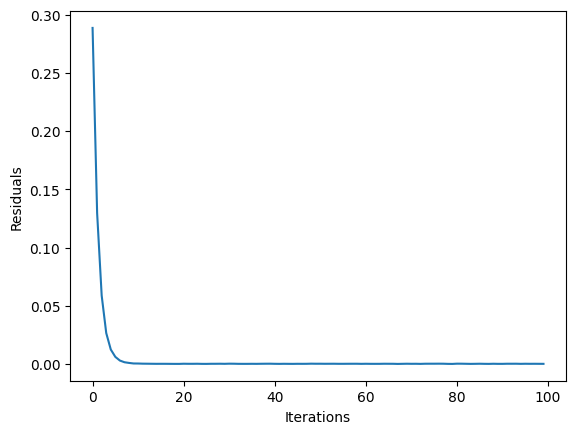
Solution statistics can be accessed in the state field and visualized. We here display the convergence of 3-ADMM-H, in terms of primal residuals.
[8]:
plt.plot(result.state.residuals)
plt.xlabel("Iterations")
plt.ylabel("Residuals")
plt.show()
Quantum Solution#
We now solve the same optimization problem with QAOA as QUBO optimizer, running on simulated quantum device. First, one need to select the classical optimizer of the eigensolver QAOA. Then, the simulation backend is set. Finally, the eigensolver is wrapped into the MinimumEigenOptimizer class. A new instance of ADMMOptimizer is populated with QAOA as QUBO optimizer.
[9]:
# define QUBO optimizer
qubo_optimizer = qaoa
# define classical optimizer
convex_optimizer = cobyla
# convex_optimizer = cplex # uncomment to use CPLEX instead
# initialize ADMM with quantum QUBO optimizer and classical convex optimizer
admm_q = ADMMOptimizer(
params=admm_params, qubo_optimizer=qubo_optimizer, continuous_optimizer=convex_optimizer
)
[10]:
# run ADMM to solve problem
result_q = admm_q.solve(qp)
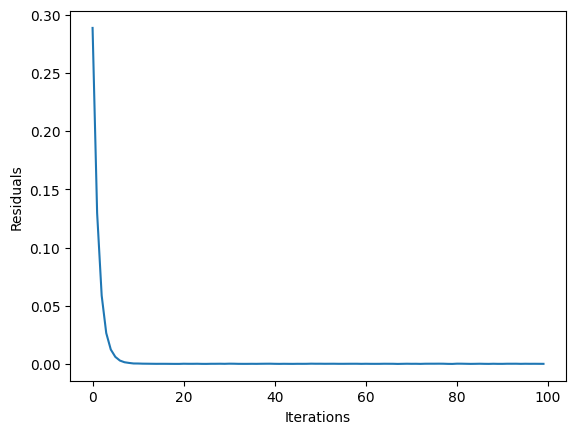
Quantum Solver Results#
Here we present the results obtained from the quantum solver. As in the example above x stands for the solution, the fval is for objective value.
[11]:
print(result.prettyprint())
objective function value: 1.0
variable values: v=1.0, w=0.0, t=0.0, u=2.0
status: SUCCESS
[12]:
plt.clf()
plt.plot(result_q.state.residuals)
plt.xlabel("Iterations")
plt.ylabel("Residuals")
plt.show()
[13]:
import tutorial_magics
%qiskit_version_table
%qiskit_copyright
Version Information
| Software | Version |
|---|---|
qiskit | 1.0.1 |
qiskit_optimization | 0.6.1 |
qiskit_algorithms | 0.3.0 |
| System information | |
| Python version | 3.8.18 |
| OS | Linux |
| Wed Feb 28 02:59:02 2024 UTC | |
This code is a part of a Qiskit project
© Copyright IBM 2017, 2024.
This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.
[ ]: