注釈
このページは docs/tutorials/10_effective_dimension.ipynb から生成されました。
Qiskitニューラルネットワークの有効な次元#
このチュートリアルでは、 EffectiveDimension クラスと LocalEffectiveDimension クラスを利用して、量子ニューラルネットワークモデルの能力を評価します。これらは、トレーニング可能性、表現可能性、一般化能力などの概念に関連する情報幾何学に基づくメトリックです。
コード例に飛び込む前に、これら2つのメトリックの違いと、それらが量子ニューラルネットワークの研究に関連する理由を簡単に説明します。グローバル有効次元の詳細については、 この論文 を参照してください。ローカル有効ディメンションは、 後の研究 で紹介されています。
1. グローバルとローカルの有効次元#
古典的な機械学習モデルと量子機械学習モデルはどちらも共通の目標を共有しています。それは 一般化 に長けていること、つまりデータから洞察を学び、それらを目に見えないデータに適用することです。
この能力を評価するための適切な指標を見つけることは重要なことです。 The Power of Quantum Neural Networks で、著者は、特定のモデルが新しいデータに対してどれだけうまく機能できるかを示す有用な指標として、グローバル な有効次元を紹介しています。 Effective Dimension of Machine Learning Models では、機械学習モデルの汎化誤差を制限する新しい容量測定値として、ローカル 有効次元が提案されています。
グローバル( EffectiveDimension クラス)と ローカル 有効ディメンション( LocalEffectiveDimension クラス)の主な違いは、実際には計算方法ではなく、分析されるパラメーター空間の性質にあります。グローバル有効次元は、モデルの 完全なパラメーター空間 を組み込み、 多数のパラメーター(重み)セット から計算されます。一方、ローカルの有効な次元は、トレーニングされた モデルが新しいデータにどれだけうまく一般化できるか、そしてそれがどれほど 表現力 があるかに焦点を当てています。したがって、局所的な有効寸法は、単一の 重みサンプルのセットから計算されます(トレーニング結果)。この違いは、実際の実装に関してはわずかですが、概念レベルでは非常に重要です。
2. 有効次元アルゴリズム#
グローバルおよびローカルの有効次元アルゴリズムはどちらも、フィッシャー情報量マトリックスを使用して複雑さの尺度を提供します。この行列の計算方法の詳細は 参考論文 に記載されていますが、一般的にこの行列は、ニューラルネットワークの出力がネットワークのパラメータ空間の変化に対してどれほど敏感であるかを示しています。
特に、このアルゴリズムは4つの主要なステップに従います。
モンテカルロシミュレーション :ニューラルネットワークの順方向パスと逆方向パス(勾配)は、入力サンプルと重みサンプルの各ペアに対して計算されます。
フィッシャー行列の計算 :これらの出力と勾配は、フィッシャー情報量の計算に使用されます。
フィッシャー行列の正規化 :すべての入力サンプルの平均と行列トレースによる除算
有効寸法の計算 : Abbas et al. の式による。
3. 基本的な例(SamplerQNN)#
この例は、QNNモデルの問題を設定し、グローバル有効次元アルゴリズムを実行する方法を示しています。Qiskit SamplerQNN``(この例に示されている)と ``EstimatorQNN (後の例に示されている)の両方を EffectiveDimension クラスで使用できます。
再現性を目的として、必要なインポートと乱数ジェネレーターの固定シードから開始します。
[1]:
# Necessary imports
import matplotlib.pyplot as plt
import numpy as np
from IPython.display import clear_output
from qiskit import QuantumCircuit
from qiskit.circuit.library import ZFeatureMap, RealAmplitudes
from qiskit_algorithms.optimizers import COBYLA
from qiskit_algorithms.utils import algorithm_globals
from sklearn.datasets import make_classification
from sklearn.preprocessing import MinMaxScaler
from qiskit_machine_learning.circuit.library import QNNCircuit
from qiskit_machine_learning.algorithms.classifiers import NeuralNetworkClassifier
from qiskit_machine_learning.neural_networks import EffectiveDimension, LocalEffectiveDimension
from qiskit_machine_learning.neural_networks import SamplerQNN, EstimatorQNN
# set random seed
algorithm_globals.random_seed = 42
3.1 QNNを定義する#
SamplerQNN を作成する最初のステップは、パラメーター化された特徴量マップとansatzを定義することです。このおもちゃの例では、3量子ビットと QNNCircuit クラスを使って、特徴量マップとansatz回路の合成を簡単にします。こうしてできた回路を SamplerQNN クラスで使います。
[2]:
num_qubits = 3
# combine a custom feature map and ansatz into a single circuit
qc = QNNCircuit(
feature_map=ZFeatureMap(feature_dimension=num_qubits, reps=1),
ansatz=RealAmplitudes(num_qubits, reps=1),
)
qc.draw("mpl")
[2]:
次に、パラメーター化された回路をオプションの解釈マップ(この場合はパリティ)と一緒に SamplerQNN コンストラクタに送信できます。
[3]:
# parity maps bitstrings to 0 or 1
def parity(x):
return "{:b}".format(x).count("1") % 2
output_shape = 2 # corresponds to the number of classes, possible outcomes of the (parity) mapping.
[4]:
# construct QNN
qnn = SamplerQNN(
circuit=qc,
interpret=parity,
output_shape=output_shape,
sparse=False,
)
3.2 実効次元計算の設定#
EffectiveDimension クラスを使用してQNNの有効次元を計算するには、一連の入力サンプルと重みのセット、およびデータセットで使用可能なデータサンプルの総数が必要です。 input_samples と weight_samples はクラスコンストラクターで設定され、データサンプルの数は有効なディメンション計算の呼び出し中に指定されるため、このメジャーがさまざまなデータセットサイズでどのように変化するかをテストおよび比較できます。
入力サンプルと重みサンプルの数を定義できます。クラスは、正規( input_samples の場合)または均一( weight_samples の場合)の分布から対応する配列をランダムにサンプリングします。 多数のサンプルを渡す代わりに、手動でサンプリングされた配列を渡すことができます。
[5]:
# we can set the total number of input samples and weight samples for random selection
num_input_samples = 10
num_weight_samples = 10
global_ed = EffectiveDimension(
qnn=qnn, weight_samples=num_weight_samples, input_samples=num_input_samples
)
入力サンプルと重みサンプルの特定のセットをテストする場合は、次のスニペットに示すように、それを EffectiveDimension クラスに直接提供できます。
[6]:
# we can also provide user-defined samples and parameters
input_samples = algorithm_globals.random.normal(0, 1, size=(10, qnn.num_inputs))
weight_samples = algorithm_globals.random.uniform(0, 1, size=(10, qnn.num_weights))
global_ed = EffectiveDimension(qnn=qnn, weight_samples=weight_samples, input_samples=input_samples)
有効な次元アルゴリズムには、データセットサイズも必要です。この例では、サイズの配列を定義して、後でこの入力が結果にどのように影響するかを確認します。
[7]:
# finally, we will define ranges to test different numbers of data, n
n = [5000, 8000, 10000, 40000, 60000, 100000, 150000, 200000, 500000, 1000000]
3.3 グローバル実効次元の計算#
次に、以前に定義した一連の入力サンプル、重み、および5000のデータセットサイズについて、ネットワークの有効な次元を計算しましょう。
[8]:
global_eff_dim_0 = global_ed.get_effective_dimension(dataset_size=n[0])
有効な次元値の範囲は0〜 d です。ここで、 d はモデルの次元を表し、実際にはQNNの重みの数から取得されます。結果を d で割ることにより、モデルの容量と直接相関する正規化された実効次元を取得できます。
[9]:
d = qnn.num_weights
print("Data size: {}, global effective dimension: {:.4f}".format(n[0], global_eff_dim_0))
print(
"Number of weights: {}, normalized effective dimension: {:.4f}".format(d, global_eff_dim_0 / d)
)
Data size: 5000, global effective dimension: 4.6657
Number of weights: 6, normalized effective dimension: 0.7776
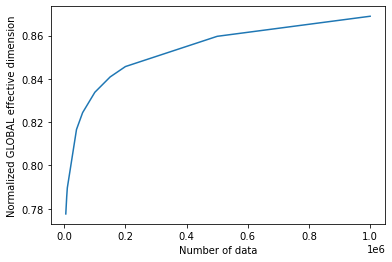
入力サイズが n の場合に配列を使用して EffectiveDimension クラスを呼び出すことにより、データセットサイズによって有効な次元がどのように変化するかを監視できます。
[10]:
global_eff_dim_1 = global_ed.get_effective_dimension(dataset_size=n)
[11]:
print("Effective dimension: {}".format(global_eff_dim_1))
print("Number of weights: {}".format(d))
Effective dimension: [4.66565096 4.7133723 4.73782922 4.89963559 4.94632272 5.00280009
5.04530433 5.07408394 5.15786005 5.21349874]
Number of weights: 6
[12]:
# plot the normalized effective dimension for the model
plt.plot(n, np.array(global_eff_dim_1) / d)
plt.xlabel("Number of data")
plt.ylabel("Normalized GLOBAL effective dimension")
plt.show()
4. ローカル有効次元の例#
はじめに説明したように、ローカル有効次元アルゴリズムは 1 セットの重みのみを使用し、トレーニングがニューラルネットワークの表現力にどのように影響するかを監視するために使用できます。 LocalEffectiveDimension クラスは、これらの計算が概念的に分離されていることを確認するためにこの制約を適用しますが、実装の残りの部分は EffectiveDimension と共有されます。
この例は、 LocalEffectiveDimension クラスを活用して、QNNの表現力に対するトレーニングの効果を分析する方法を示しています。
4.1 データセットとQNNの定義#
まず、scikit-learnの make_classification 関数を用いて、3Dバイナリー分類データセットを作成することから始めます。
[13]:
num_inputs = 3
num_samples = 50
X, y = make_classification(
n_samples=num_samples,
n_features=num_inputs,
n_informative=3,
n_redundant=0,
n_clusters_per_class=1,
class_sep=2.0,
)
X = MinMaxScaler().fit_transform(X)
y = 2 * y - 1 # labels in {-1, 1}
次のステップはQNNを作成することで、この場合は EstimatorQNN のインスタンスを SamplerQNN のインスタンスと同じ方法で作成します。
[14]:
estimator_qnn = EstimatorQNN(circuit=qc)
4.2 QNNのトレーニング#
これで、QNNのトレーニングに進むことができます。トレーニングステップには時間がかかる場合があります。しばらくお待ちください。 分類器にコールバックを渡して、トレーニングプロセスがどのように進行しているかを観察できます。 通常どおり、再現性のために initial_point を修正します。
[15]:
# callback function that draws a live plot when the .fit() method is called
def callback_graph(weights, obj_func_eval):
clear_output(wait=True)
objective_func_vals.append(obj_func_eval)
plt.title("Objective function value against iteration")
plt.xlabel("Iteration")
plt.ylabel("Objective function value")
plt.plot(range(len(objective_func_vals)), objective_func_vals)
plt.show()
[16]:
# construct classifier
initial_point = algorithm_globals.random.random(estimator_qnn.num_weights)
estimator_classifier = NeuralNetworkClassifier(
neural_network=estimator_qnn,
optimizer=COBYLA(maxiter=80),
initial_point=initial_point,
callback=callback_graph,
)
[17]:
# create empty array for callback to store evaluations of the objective function (callback)
objective_func_vals = []
plt.rcParams["figure.figsize"] = (12, 6)
# fit classifier to data
estimator_classifier.fit(X, y)
# return to default figsize
plt.rcParams["figure.figsize"] = (6, 4)
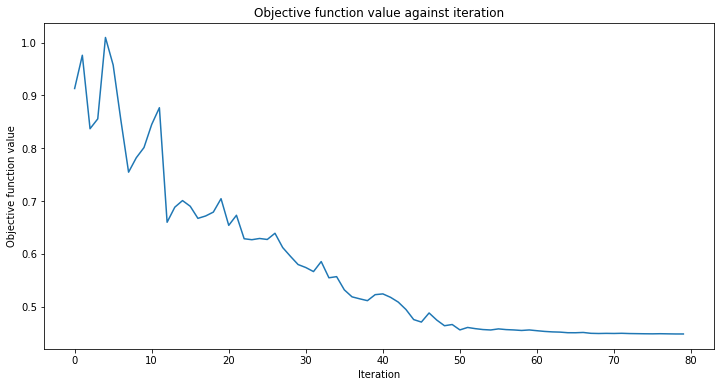
分類器は、次の精度でクラスを区別できるようになりました。
[18]:
# score classifier
estimator_classifier.score(X, y)
[18]:
0.96
4.3 トレーニングされたQNNのローカル有効次元を計算する#
ネットワークをトレーニングしたので、トレーニングした重みに基づいてローカルの有効次元を評価しましょう。そのために、分類器から直接トレーニング済みの重みにアクセスします。
[19]:
trained_weights = estimator_classifier.weights
# get Local Effective Dimension for set of trained weights
local_ed_trained = LocalEffectiveDimension(
qnn=estimator_qnn, weight_samples=trained_weights, input_samples=X
)
local_eff_dim_trained = local_ed_trained.get_effective_dimension(dataset_size=n)
print(
"normalized local effective dimensions for trained QNN: ",
local_eff_dim_trained / estimator_qnn.num_weights,
)
normalized local effective dimensions for trained QNN: [0.38001027 0.38667693 0.39017714 0.41507888 0.42307677 0.43341398
0.44170977 0.44758111 0.46577231 0.4786767 ]
4.4 トレーニングされていないQNNのローカル有効次元を計算する#
重みのサンプルとして initial_point を使用して、この結果をトレーニングされていないネットワークの有効な次元と比較できます。
[20]:
# get Local Effective Dimension for set of untrained weights
local_ed_untrained = LocalEffectiveDimension(
qnn=estimator_qnn, weight_samples=initial_point, input_samples=X
)
local_eff_dim_untrained = local_ed_untrained.get_effective_dimension(dataset_size=n)
print(
"normalized local effective dimensions for untrained QNN: ",
local_eff_dim_untrained / estimator_qnn.num_weights,
)
normalized local effective dimensions for untrained QNN: [0.69803061 0.7130991 0.7203237 0.76321615 0.77452215 0.7877625
0.79746712 0.8039319 0.82236146 0.83435907]
4.5 結果のプロットと分析#
トレーニングの前後の実効次元値をプロットすると、次の結果が得られます。
[21]:
# plot the normalized effective dimension for the model
plt.plot(n, np.array(local_eff_dim_trained) / estimator_qnn.num_weights, label="trained weights")
plt.plot(
n, np.array(local_eff_dim_untrained) / estimator_qnn.num_weights, label="untrained weights"
)
plt.xlabel("Number of data")
plt.ylabel("Normalized LOCAL effective dimension")
plt.legend()
plt.show()
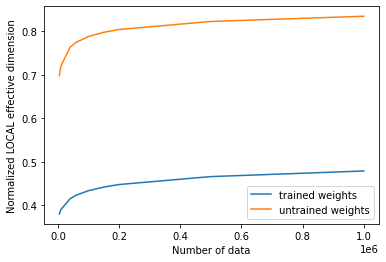
一般に、トレーニング後にローカル有効次元の値が減少することを期待する必要があります。これは、機械学習の主な目標を振り返ることで理解できます。これは、データに適合するのに十分な表現力があるが、新しいデータサンプルに適合しすぎてパフォーマンスが悪いほど表現力のないモデルを選択することです。
特定のオプティマイザは、パラメータを学習することでモデルの過剰適合を正規化するのに役立ちます。この学習アクションは、ローカルの有効次元で測定されるように、モデルの表現力を本質的に低下させます。このロジックに従うと、ランダムに初期化されたパラメーターセットは、トレーニングされた重みの最終セットよりも有効な次元を生成する可能性が高くなります。これは、その特定のパラメーター化を使用したモデルが、データを適合させるために不必要に「より多くのパラメーターを使用する」ためです。 トレーニング後(暗黙の正則化を使用)、トレーニングされたモデルはそれほど多くのパラメーターを使用する必要がないため、「非アクティブなパラメーター」が多くなり、有効な次元が低くなります。
これは一般的な洞察であり、あるモデルの訓練された重みよりもランダムに選ばれた重みが偶然低い有効次元を提供するなど、さまざまな場合がありうることに留意しなければなりません。
[22]:
import qiskit.tools.jupyter
%qiskit_version_table
%qiskit_copyright
Version Information
| Qiskit Software | Version |
|---|---|
qiskit-terra | 0.24.0 |
qiskit-aer | 0.12.0 |
qiskit-ignis | 0.6.0 |
qiskit-ibmq-provider | 0.20.2 |
qiskit | 0.43.0 |
qiskit-machine-learning | 0.7.0 |
| System information | |
| Python version | 3.8.8 |
| Python compiler | Clang 10.0.0 |
| Python build | default, Apr 13 2021 12:59:45 |
| OS | Darwin |
| CPUs | 8 |
| Memory (Gb) | 32.0 |
| Tue Jun 13 16:40:08 2023 CEST | |
This code is a part of Qiskit
© Copyright IBM 2017, 2023.
This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.