Note
Cette page a été générée à partir de ` docs/tutorials/01_neural_networks.ipynb ` __.
Réseaux de neurones quantiques#
Vue d’ensemble#
Ce bloc-notes montre différentes implémentations de réseau de neurones quantique (QNN) fournies dans qiskit-machine-learning, et comment elles peuvent être intégrées dans des processus de travail de base en apprentissage automatique quantique (QML).
Le tutoriel est structuré comme suit :
Comment instancier des QNNs
Comment exécuter un Forward Pass
Comment réaliser la backpropagation
Fonctionnalités avancées
1. Introduction#
1.1. Les différences entre les réseaux de neurones quantiques et classiques#
Les réseaux neuronaux classiques sont des modèles algorithmiques inspirés du cerveau humain qui peuvent être entraînés pour reconnaître des motifs dans des données et apprendre à résoudre des problèmes complexes. Ils sont basés sur une série de nœuds interconnectés, ou neurones, organisés dans une structure en couches avec des paramètres pouvant être appris en appliquant des algorithmes d’entraînement issus du domaine de l’apprentissage automatique.
La motivation qui sous-tend l’apprentissage automatique quantique (QML) est d’intégrer les notions de l’informatique quantique et de l’apprentissage automatique classique pour ouvrir la voie à de nouveaux programmes d’apprentissage améliorés. Les QNN appliquent ce principe générique en combinant les réseaux neuronaux classiques et les circuits quantiques paramétrés. Parce qu’ils se trouvent à une intersection entre deux champs, les QNN peuvent être vus de deux points de vue :
Du point de vue de l’apprentissage automatique, les QNNs sont, une fois de plus, des modèles algorithmiques qui peuvent être formés pour trouver des modèles cachés dans les données de la même manière que leurs homologues classiques. Ces modèles peuvent charger (load) des données classiques (** inputs**) dans un état quantique, et plus tard effectuer des calculs (process) avec des portes quantiques dépendants de paramétrées entrainés. La figure 1 montre un exemple de QNN générique, y compris les étapes de chargement et de traitement des données. La sortie de la mesure de cet état peut alors être insérée dans une fonction de perte pour former les poids par rétropropagation.
Du point de vue de l’informatique quantique , les QNNs sont des algorithmes quantiques basés sur des circuits quantiques paramétrés qui peuvent être entrainés de manière variationnelle en utilisant des optimiseurs classiques. Ces circuits contiennent une carte des features (avec des paramètres d’entrée) et un ** ansatz** (avec des poids entrainables), comme le montre la figure 1.
*Figure 1. Structure du réseau de neurones quantiques générique (QNN) *
Comme vous pouvez le constater, ces deux perspectives sont complémentaires et ne reposent pas nécessairement sur des définitions strictes de concepts tels que le « neurone quantique » ou ce qui constitue une « couche » de QNN.
1.2. Implementation in qiskit-machine-learning#
Les QNNs dans qiskit-machine-learning sont des unités de calcul agnostiques d’application qui peuvent être utilisées pour différents cas d’utilisation, et leur configuration dépendra de l’application pour laquelle ils sont nécessaires. Le module contient une interface pour les QNNs et deux implémentations spécifiques:
NeuralNetwork: The interface for neural networks. This is an abstract class all QNNs inherit from.
EstimatorQNN: A network based on the evaluation of quantum mechanical observables.
SamplerQNN: A network based on the samples resulting from measuring a quantum circuit.
Ces implémentations sont basées sur les primitives qiskit <https://qiskit.org/documentation/apidoc/primitives.html> __. Les primitives sont le point d’entrée permettant d’exécuter des QNNs sur un simulateur ou un matériel quantique réel. Chaque implémentation, EstimatorQNN et SamplerQNN, prend une instance facultative de sa primitive correspondante, qui peut être n’importe quelle sous-classe de BaseEstimator et BaseSampler, respectivement.
Le module qiskit.primitives fournit une implémentation de référence pour les classes Sampler et Estimator pour exécuter des simulations avec état. Par défaut, si aucune instance n’est transmise à une classe QNN, une instance de la primitive de référence correspondante (Sampler ou Estimator) est créée automatiquement par le réseau. Pour plus d’informations sur les primitives, reportez-vous à la documentation des primitives <https://qiskit.org/documentation/apidoc/primitives.html>` __.
La classe NeuralNetwork est l’interface pour tous les QNNs disponibles dans qiskit-machine-learning. Elle expose un passage à l’avant et un passe arrière qui prennent des échantillons de données et des poids de formation en entrée.
It’s important to note that NeuralNetworks are « stateless ». They do not contain any training capabilities (these are pushed to the actual algorithms or applications: classifiers, regressors, etc), nor do they store the values for trainable weights.
Examinons maintenant des exemples spécifiques pour les deux implémentations de NeuralNetwork. Mais d’abord, fixons la graine algorithmique (seed) pour s’assurer que les résultats ne changent pas entre les exécutions.
[25]:
from qiskit_algorithms.utils import algorithm_globals
algorithm_globals.random_seed = 42
2. Comment instancier les QNNs#
2.1. EstimatorQNN#
Le EstimatorQNN prend un circuit quantique paramétré comme entrée, ainsi qu’un calcul quantique optionnel observable, et des calculs de la valeur des attentes de sortie pour le passage à terme. Le EstimatorQNN' accepte également des listes d’observables pour construire des QNNs plus complexes.
Voyons un EstimatorQNN en action avec un exemple simple. Nous commençons par construire le circuit paramétré. Ce circuit quantique a deux paramètres, l’un représente une entrée QNN et l’autre représente un poids entrainable:
[26]:
from qiskit.circuit import Parameter
from qiskit import QuantumCircuit
params1 = [Parameter("input1"), Parameter("weight1")]
qc1 = QuantumCircuit(1)
qc1.h(0)
qc1.ry(params1[0], 0)
qc1.rx(params1[1], 0)
qc1.draw("mpl")
[26]:
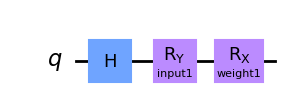
Nous pouvons maintenant créer une valeur observable pour définir le calcul de la valeur de l’espérance. Si ce n’est pas le cas, le EstimatorQNN va automatiquement créer la valeur par défaut \(Z^{\otimes n }\). Ici, \(n\) est le nombre de qubits du circuit quantique.
Dans cet exemple, nous allons changer les choses et utiliser l’obervable \(Y^{ \otimes n}\) :
[27]:
from qiskit.quantum_info import SparsePauliOp
observable1 = SparsePauliOp.from_list([("Y" * qc1.num_qubits, 1)])
Avec le circuit quantique défini ci-dessus et l’observation que nous avons créée, le constructeur EstimatorQNN admet les arguments de mots clés suivants :
estimator: instance primitive facultativeinput_params: liste des paramètres de circuit quantique qui doivent être traités comme des « entrées réseau »weight_params: liste des paramètres de circuit quantique qui doivent être traités comme des « poids réseau »
Dans cet exemple, nous avons précédemment décidé que le premier paramètre de params1 devrait être l’entrée, tandis que le second devrait être le poids. Au fur et à mesure que nous exécutons une simulation d’un vecteur local, nous n’allons pas définir le paramètre estimateur ; le réseau va créer une instance de la référence Estimateur pour nous. Si nous avions besoin d’accéder aux ressources dans le Cloud ou aux simulateurs Aer, nous devons définir les instances Estimator respectives et les transmettre au EstimatorQNN.
[28]:
from qiskit_machine_learning.neural_networks import EstimatorQNN
estimator_qnn = EstimatorQNN(
circuit=qc1, observables=observable1, input_params=[params1[0]], weight_params=[params1[1]]
)
estimator_qnn
[28]:
<qiskit_machine_learning.neural_networks.estimator_qnn.EstimatorQNN at 0x7fd668ca0e80>
Nous verrons comment utiliser le QNN dans les sections suivantes, mais avant ça, allons voir la classe SamplerQNN.
2.2. SamplerQNN#
Le SamplerQNN est instancié de manière similaire à EstimatorQNN, mais parce qu’il consomme directement des échantillons de la mesure du circuit quantique, il n’a pas besoin d’un observable spécifique.
Ces exemples de sortie sont interprétés par défaut comme étant les probabilités de mesure de l’index entier correspondant à une chaîne de bits. Cependant, le SamplerQNN nous permet également de spécifier une fonction d’intreprétation interpret pour le post-traitement des échantillons. Cette fonction doit être définie de sorte qu’elle prenne un entier mesuré (à partir d’une chaîne de bits) et la mappe à une nouvelle valeur, c’est-à-dire un entier non négatif.
(!) Il est important de noter que si une fonction personnalisée interpret est définie, la forme output_shape ne peut pas être déduite par le réseau et doit être fournie explicitement.
(!) Il est également important de garder à l’esprit que si aucune fonction interpret n’est utilisée, la dimension du vecteur de probabilité croît exponentiellement avec le nombre de qubits. Avec une fonction d’interprétation personnalisée, cette mise à l’échelle peut changer. Si, par exemple, un index est mappé à la parité de la chaîne de bits correspondante, c’est-à-dire à 0 ou 1, le résultat sera un vecteur de probabilité de longueur 2 indépendamment du nombre de qubits.
Nous allons créer un circuit quantique différent pour le SamplerQNN. Dans ce cas, nous aurons deux paramètres d’entrée et quatre poids de formation qui paramétreront un circuit two-local.
[29]:
from qiskit.circuit import ParameterVector
inputs2 = ParameterVector("input", 2)
weights2 = ParameterVector("weight", 4)
print(f"input parameters: {[str(item) for item in inputs2.params]}")
print(f"weight parameters: {[str(item) for item in weights2.params]}")
qc2 = QuantumCircuit(2)
qc2.ry(inputs2[0], 0)
qc2.ry(inputs2[1], 1)
qc2.cx(0, 1)
qc2.ry(weights2[0], 0)
qc2.ry(weights2[1], 1)
qc2.cx(0, 1)
qc2.ry(weights2[2], 0)
qc2.ry(weights2[3], 1)
qc2.draw(output="mpl")
input parameters: ['input[0]', 'input[1]']
weight parameters: ['weight[0]', 'weight[1]', 'weight[2]', 'weight[3]']
[29]:
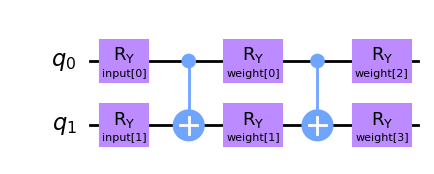
De même que le EstimatorQNN, nous devons spécifier des entrées et des poids lors de l’instanciation du SamplerQNN. Dans ce cas, les arguments du mot clé seront: -sampler: instance primitive facultative -input_params: liste des paramètres de circuit quantique qui doivent être traités comme des « entrées réseau »- weight_params: liste des paramètres de circuit quantique qui doivent être traités comme des « poids réseau »
Veuillez noter que, une fois de plus, nous choisissons de ne pas fixer l’instance Sampler au QNN et de compter sur la valeur par défaut.
[30]:
from qiskit_machine_learning.neural_networks import SamplerQNN
sampler_qnn = SamplerQNN(circuit=qc2, input_params=inputs2, weight_params=weights2)
sampler_qnn
[30]:
<qiskit_machine_learning.neural_networks.sampler_qnn.SamplerQNN at 0x7fd659264880>
En plus des arguments de base montrés ci-dessus, SamplerQNN accepte trois autres réglages: input_gradients, interpret et output_shape. Ils seront introduits dans les sections 4 et 5.
3. Comment exécuter un passage vers l’avant (forward pass)#
3.1. Paramétrage#
Dans un contexte réel, les entrées seraient définies par le jeu de données, et les pondérations seraient définies par l’algorithme d’entraînement ou dans le cadre d’un modèle préentraîné. Toutefois, dans l’intérêt de ce tutoriel, nous allons spécifier des ensembles aléatoires d’entrée et de pondération de la bonne dimension :
3.1.1. Exemple de EstimatorQNN#
[31]:
estimator_qnn_input = algorithm_globals.random.random(estimator_qnn.num_inputs)
estimator_qnn_weights = algorithm_globals.random.random(estimator_qnn.num_weights)
[32]:
print(
f"Number of input features for EstimatorQNN: {estimator_qnn.num_inputs} \nInput: {estimator_qnn_input}"
)
print(
f"Number of trainable weights for EstimatorQNN: {estimator_qnn.num_weights} \nWeights: {estimator_qnn_weights}"
)
Number of input features for EstimatorQNN: 1
Input: [0.77395605]
Number of trainable weights for EstimatorQNN: 1
Weights: [0.43887844]
3.1.2. Exemple de SamplerQNN#
[33]:
sampler_qnn_input = algorithm_globals.random.random(sampler_qnn.num_inputs)
sampler_qnn_weights = algorithm_globals.random.random(sampler_qnn.num_weights)
[34]:
print(
f"Number of input features for SamplerQNN: {sampler_qnn.num_inputs} \nInput: {sampler_qnn_input}"
)
print(
f"Number of trainable weights for SamplerQNN: {sampler_qnn.num_weights} \nWeights: {sampler_qnn_weights}"
)
Number of input features for SamplerQNN: 2
Input: [0.85859792 0.69736803]
Number of trainable weights for SamplerQNN: 4
Weights: [0.09417735 0.97562235 0.7611397 0.78606431]
Une fois que nous avons les entrées et les poids, voyons les résultats pour les passes batchées et non batchées.
3.2. Forward pass non batché#
3.2.1. Exemple de EstimatorQNN#
Pour EstimatorQNN, la forme de sortie attendue pour le passage à terme est (1, num_qubits * num_observables) où 1 dans notre cas est le nombre d’échantillons :
[35]:
estimator_qnn_forward = estimator_qnn.forward(estimator_qnn_input, estimator_qnn_weights)
print(
f"Forward pass result for EstimatorQNN: {estimator_qnn_forward}. \nShape: {estimator_qnn_forward.shape}"
)
Forward pass result for EstimatorQNN: [[0.2970094]].
Shape: (1, 1)
3.2.2. Exemple de SamplerQNN#
Pour le SamplerQNN (sans fonction d’interprétation personnalisée), la forme de sortie attendue pour le passage à terme est (1, 2 **num_qubits). Avec une fonction d’interprétation personnalisée, la forme de sortie sera (1, output_shape), où 1 dans notre cas est le nombre d’échantillons :
[36]:
sampler_qnn_forward = sampler_qnn.forward(sampler_qnn_input, sampler_qnn_weights)
print(
f"Forward pass result for SamplerQNN: {sampler_qnn_forward}. \nShape: {sampler_qnn_forward.shape}"
)
Forward pass result for SamplerQNN: [[0.01826527 0.25735654 0.5267981 0.19758009]].
Shape: (1, 4)
3.3. Forward pass batché#
3.3.1. Exemple de EstimatorQNN#
Pour EstimatorQNN, la forme de sortie attendue pour le passforward est (batch_size, num_qubits * num_observables) :
[37]:
estimator_qnn_forward_batched = estimator_qnn.forward(
[estimator_qnn_input, estimator_qnn_input], estimator_qnn_weights
)
print(
f"Forward pass result for EstimatorQNN: {estimator_qnn_forward_batched}. \nShape: {estimator_qnn_forward_batched.shape}"
)
Forward pass result for EstimatorQNN: [[0.2970094]
[0.2970094]].
Shape: (2, 1)
3.3.2. Exemple de SamplerQNN#
Pour SamplerQNN (sans fonction d’interprétation personnalisée), la forme de sortie attendue pour le forward pass est (batch_size, 2**num_qubits). Avec une fonction d’interprétation personnalisée, la forme de sortie sera (batch_size, output_shape).
[38]:
sampler_qnn_forward_batched = sampler_qnn.forward(
[sampler_qnn_input, sampler_qnn_input], sampler_qnn_weights
)
print(
f"Forward pass result for SamplerQNN: {sampler_qnn_forward_batched}. \nShape: {sampler_qnn_forward_batched.shape}"
)
Forward pass result for SamplerQNN: [[0.01826527 0.25735654 0.5267981 0.19758009]
[0.01826527 0.25735654 0.5267981 0.19758009]].
Shape: (2, 4)
4. Comment exécuter un passage arrière (Backward Pass, rétropropagation)#
Let’s take advantage of the inputs and weights defined above to show how the backward pass works. This pass returns a tuple (input_gradients, weight_gradients). By default, the backward pass will only calculate gradients with respect to the weight parameters.
If you want to enable gradients with respect to the input parameters, you should set the following flag during the QNN instantiation:
qnn = ...QNN(..., input_gradients=True)
Please remember that input gradients are required for the use of TorchConnector for PyTorch integration.
4.1. Backward Pass without Input Gradients#
4.1.1. EstimatorQNN Example#
For the EstimatorQNN, the expected output shape for the weight gradients is (batch_size, num_qubits * num_observables, num_weights):
[39]:
estimator_qnn_input_grad, estimator_qnn_weight_grad = estimator_qnn.backward(
estimator_qnn_input, estimator_qnn_weights
)
print(
f"Input gradients for EstimatorQNN: {estimator_qnn_input_grad}. \nShape: {estimator_qnn_input_grad}"
)
print(
f"Weight gradients for EstimatorQNN: {estimator_qnn_weight_grad}. \nShape: {estimator_qnn_weight_grad.shape}"
)
Input gradients for EstimatorQNN: None.
Shape: None
Weight gradients for EstimatorQNN: [[[0.63272767]]].
Shape: (1, 1, 1)
4.1.2. SamplerQNN Example#
For the SamplerQNN (without custom interpret function), the expected output shape for the forward pass is (batch_size, 2**num_qubits, num_weights). With a custom interpret function, the output shape will be (batch_size, output_shape, num_weights).:
[40]:
sampler_qnn_input_grad, sampler_qnn_weight_grad = sampler_qnn.backward(
sampler_qnn_input, sampler_qnn_weights
)
print(
f"Input gradients for SamplerQNN: {sampler_qnn_input_grad}. \nShape: {sampler_qnn_input_grad}"
)
print(
f"Weight gradients for SamplerQNN: {sampler_qnn_weight_grad}. \nShape: {sampler_qnn_weight_grad.shape}"
)
Input gradients for SamplerQNN: None.
Shape: None
Weight gradients for SamplerQNN: [[[ 0.00606238 -0.1124595 -0.06856156 -0.09809236]
[ 0.21167414 -0.09069775 0.06856156 -0.22549618]
[-0.48846674 0.32499215 -0.32262178 0.09809236]
[ 0.27073021 -0.12183491 0.32262178 0.22549618]]].
Shape: (1, 4, 4)
4.2. Backward Pass with Input Gradients#
Let’s enable the input_gradients to show what the expected output sizes are for this option.
[41]:
estimator_qnn.input_gradients = True
sampler_qnn.input_gradients = True
4.2.1. EstimatorQNN Example#
For the EstimatorQNN, the expected output shape for the input gradients is (batch_size, num_qubits * num_observables, num_inputs):
[42]:
estimator_qnn_input_grad, estimator_qnn_weight_grad = estimator_qnn.backward(
estimator_qnn_input, estimator_qnn_weights
)
print(
f"Input gradients for EstimatorQNN: {estimator_qnn_input_grad}. \nShape: {estimator_qnn_input_grad.shape}"
)
print(
f"Weight gradients for EstimatorQNN: {estimator_qnn_weight_grad}. \nShape: {estimator_qnn_weight_grad.shape}"
)
Input gradients for EstimatorQNN: [[[0.3038852]]].
Shape: (1, 1, 1)
Weight gradients for EstimatorQNN: [[[0.63272767]]].
Shape: (1, 1, 1)
4.2.2. SamplerQNN Example#
For the SamplerQNN (without custom interpret function), the expected output shape for the input gradients is (batch_size, 2**num_qubits, num_inputs). With a custom interpret function, the output shape will be (batch_size, output_shape, num_inputs).
[43]:
sampler_qnn_input_grad, sampler_qnn_weight_grad = sampler_qnn.backward(
sampler_qnn_input, sampler_qnn_weights
)
print(
f"Input gradients for SamplerQNN: {sampler_qnn_input_grad}. \nShape: {sampler_qnn_input_grad.shape}"
)
print(
f"Weight gradients for SamplerQNN: {sampler_qnn_weight_grad}. \nShape: {sampler_qnn_weight_grad.shape}"
)
Input gradients for SamplerQNN: [[[-0.05844702 -0.10621091]
[ 0.38798796 -0.19544083]
[-0.34561132 0.09459601]
[ 0.01607038 0.20705573]]].
Shape: (1, 4, 2)
Weight gradients for SamplerQNN: [[[ 0.00606238 -0.1124595 -0.06856156 -0.09809236]
[ 0.21167414 -0.09069775 0.06856156 -0.22549618]
[-0.48846674 0.32499215 -0.32262178 0.09809236]
[ 0.27073021 -0.12183491 0.32262178 0.22549618]]].
Shape: (1, 4, 4)
5. Advanced Functionality#
5.1. EstimatorQNN with Multiple Observables#
The EstimatorQNN allows to pass lists of observables for more complex QNN architectures. For example (note the change in output shape):
[44]:
observable2 = SparsePauliOp.from_list([("Z" * qc1.num_qubits, 1)])
estimator_qnn2 = EstimatorQNN(
circuit=qc1,
observables=[observable1, observable2],
input_params=[params1[0]],
weight_params=[params1[1]],
)
[45]:
estimator_qnn_forward2 = estimator_qnn2.forward(estimator_qnn_input, estimator_qnn_weights)
estimator_qnn_input_grad2, estimator_qnn_weight_grad2 = estimator_qnn2.backward(
estimator_qnn_input, estimator_qnn_weights
)
print(f"Forward output for EstimatorQNN1: {estimator_qnn_forward.shape}")
print(f"Forward output for EstimatorQNN2: {estimator_qnn_forward2.shape}")
print(f"Backward output for EstimatorQNN1: {estimator_qnn_weight_grad.shape}")
print(f"Backward output for EstimatorQNN2: {estimator_qnn_weight_grad2.shape}")
Forward output for EstimatorQNN1: (1, 1)
Forward output for EstimatorQNN2: (1, 2)
Backward output for EstimatorQNN1: (1, 1, 1)
Backward output for EstimatorQNN2: (1, 2, 1)
5.2. SamplerQNN with custom interpret#
One common interpret method for SamplerQNN is the parity function, which allows it to perform binary classification. As explained in the instantiation section, using interpret functions will modify the output shape of the forward and backward passes. In the case of the parity interpret function, output_shape is fixed to 2. Therefore, the expected forward and weight gradient shapes are (batch_size, 2) and (batch_size, 2, num_weights), respectively:
[46]:
parity = lambda x: "{:b}".format(x).count("1") % 2
output_shape = 2 # parity = 0, 1
sampler_qnn2 = SamplerQNN(
circuit=qc2,
input_params=inputs2,
weight_params=weights2,
interpret=parity,
output_shape=output_shape,
)
[47]:
sampler_qnn_forward2 = sampler_qnn2.forward(sampler_qnn_input, sampler_qnn_weights)
sampler_qnn_input_grad2, sampler_qnn_weight_grad2 = sampler_qnn2.backward(
sampler_qnn_input, sampler_qnn_weights
)
print(f"Forward output for SamplerQNN1: {sampler_qnn_forward.shape}")
print(f"Forward output for SamplerQNN2: {sampler_qnn_forward2.shape}")
print(f"Backward output for SamplerQNN1: {sampler_qnn_weight_grad.shape}")
print(f"Backward output for SamplerQNN2: {sampler_qnn_weight_grad2.shape}")
Forward output for SamplerQNN1: (1, 4)
Forward output for SamplerQNN2: (1, 2)
Backward output for SamplerQNN1: (1, 4, 4)
Backward output for SamplerQNN2: (1, 2, 4)
6. Conclusion#
In this tutorial, we introduced the two neural networks classes provided by qiskit-machine-learning, namely the EstimatorQNN and SamplerQNN, which extend the base NeuralNetwork class. We provided some theoretical background, the key steps for QNN initialization, basic use in forward and backward passes, and advanced functionality.
We now encourage you to play around with the problem setup and see how different circuit sizes, input, and weight parameter lengths influence the output shapes.
[48]:
import qiskit.tools.jupyter
%qiskit_version_table
%qiskit_copyright
Version Information
| Qiskit Software | Version |
|---|---|
qiskit-terra | 0.22.3 |
qiskit-machine-learning | 0.6.0 |
| System information | |
| Python version | 3.9.15 |
| Python compiler | Clang 14.0.6 |
| Python build | main, Nov 24 2022 08:29:02 |
| OS | Darwin |
| CPUs | 8 |
| Memory (Gb) | 64.0 |
| Mon Jan 23 11:57:49 2023 CET | |
This code is a part of Qiskit
© Copyright IBM 2017, 2023.
This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.
Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.